Метод параллельного переноса решения геометрических задач

Переносом Т плоскости на заданный вектор называется преобразование плоскости, которое каждую точку М отображает на такую точку М, что MM' = r.
Это определение оправдано тем, что отображение, удовлетворяющее указанным в нем двум требованиям, отображает плоскость на себя и обратно, т.е. является преобразованием плоскости
Теорема. Перенос есть движение.
ЕслиТr(М) = М и Тr(N) = N, тоMM=NN=r
Следовательно, MM' + M'N = M'N + NN', или MN = M'N' и, значит, MN = M'N'
Сравнение ориентаций двух соответственных при переносе треугольников показывает, что перенос является движением первого рода

Любой параллельный перенос можно представить как композицию двух осевых симметрий с параллельными осями, причем направление осей перпендикулярно переносу, а расстояние между ними равно половине его длины.

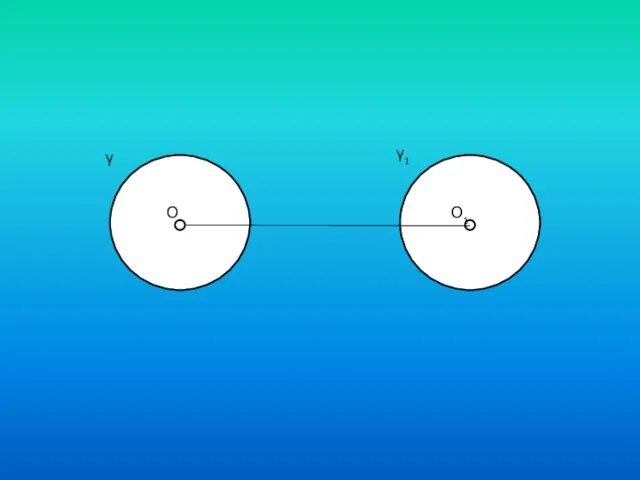
ЗАДАЧА.
Постройте прямую, которая пересекает по равным хордам два равных круга.
Дано: γ (О,r); γ1 (O, r).
Анализ.
Пусть s – искомая прямая, тогда s ∩ γ = {A,B}, s ∩ γ1 = {A1, B1} и АВ = А1В1.
Тогда ∆АОВ = ∆А1О1В1 (ОА = О1А1 = r, ОВ = О1В1 = r, АВ = А1В1), отсюда ОАВ = О1А1В1;
но А, В, А1, В1 є s, следовательно, ОА || О1А1.
Поэтому АОО1А1 – параллелограмм ( ОА = О1А1, ОА || О1А1), отсюда s || ОО1
Построение.
1.ОО1
2.р: О є р, р ОО1
3.р ∩ γ = {C, D}.
4.А: А є γ, А ≠ C, D.
5.s: A є s, s || OO1
6.s – искомая прямая.

γ
γ1
О
О1

γ
γ1
О
О1

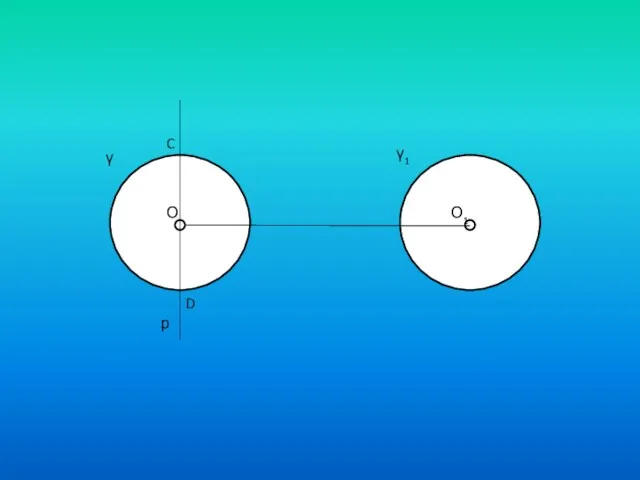
γ
γ1
О
О1
р
C
D

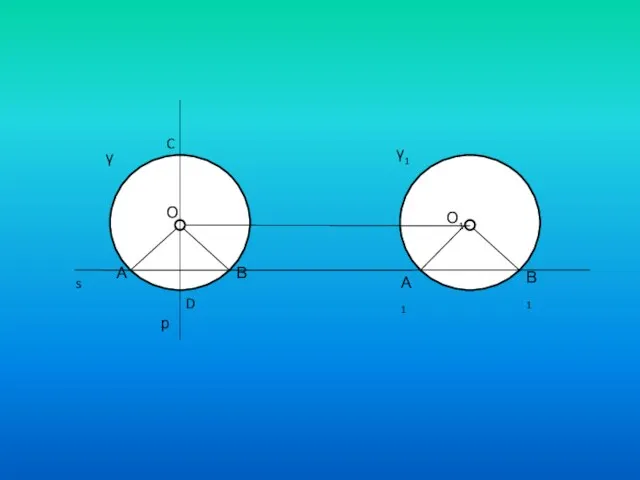
γ
γ1
О
О1
р
C
D
А
s
В
А1
В1