Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем

Актуальность работы
Манипулятор с рабочим органом в виде вязкоупругого стержня – сложная комбинированная система, состоящая из сосредоточенных и распределенных элементов. Для синтеза регулятора таких систем используются методы параметрической оптимизации, которые сложны и не наглядны.
Является актуальным использовать для синтеза регулятора таких систем хорошо известный инженерам и наглядный метод логарифмических амплитудных и фазовых частотных характеристик.

Цель работы
Целью работы является исследование возможности применения метода логарифмических амплитудно-частотных характеристик для синтеза регулятора системы управления манипулятором с упругим стержнем.

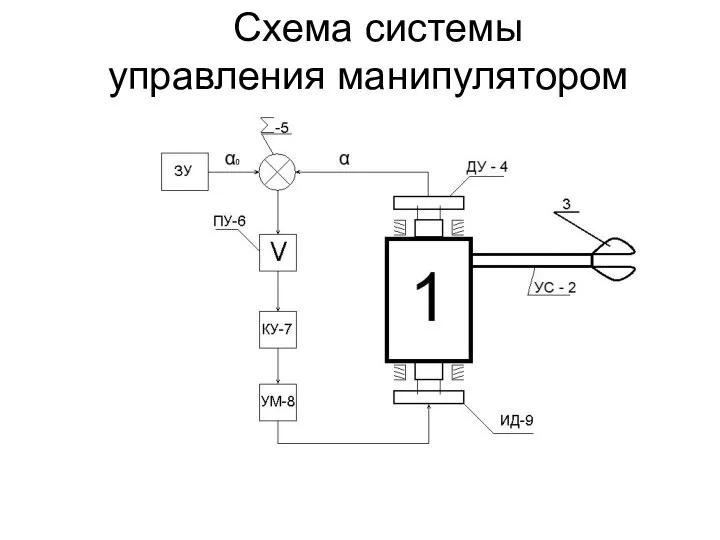
Схема системы управления манипулятором

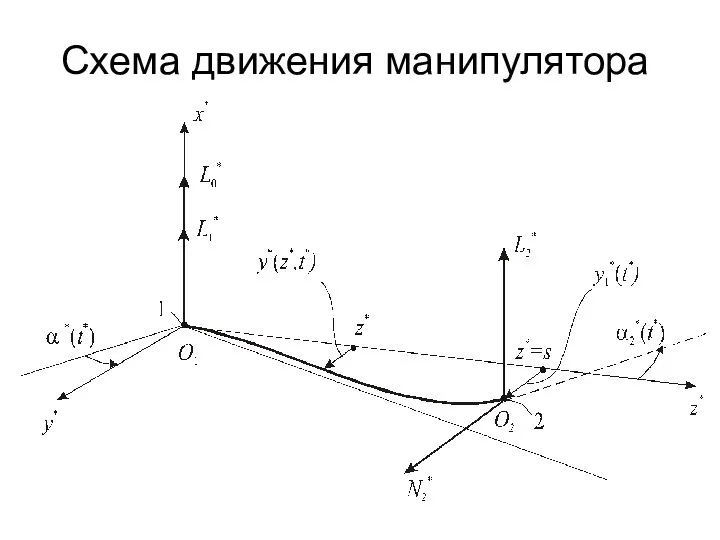
Схема движения манипулятора

Уравнения движения манипулятора в размерной форме

Уравнения движения манипулятора в размерной форме

Приведение уравнений к безразмерной форме
Известно , что в гибких стержнях характерные процессы определяются такими параметрами стержней и их материала:
E – модуль Юнга упругости материала;
J – момент инерции поперечного сечения стержня;
s – длина стержня;
ρ – плотность материала стержня.
Их этих параметров можно составить комбинацию имеющую размерность времени
Эта комбинация представляет собой характерное время протекающих в стержнях процессов

Приведение уравнений к безразмерной форме
Имея единый масштаб длины можно ввести безразмерные переменные
y1 =y1*/ δ , y1- безразмерное упругое перемещение конца стержня;
y =y*/ δ, y – безразмерный прогиб стержня;
z=z*/ s, z – безразмерная координата поперечного сечения стержня.

Уравнения движения манипулятора в безразмерной форме
Обыкновенные дифференциальные уравнения движения абсолютно твердых вала и исполнительного органа.
Дифференциальное уравнение с частными производными, моделирующее процессы изгиба стержня.
Граничные условия.
Начальные условия.
Уравнения связи абсолютно твердых вала и исполнительного органа через гибкий стержень.

Уравнения системы управления манипулятором в изображениях

Передаточные функции замкнутой и разомкнутой систем стабилизации манипулятора
Структурная схема системы стабилизации манипулятора с регулятором самого общего вида
передаточная функция замкнутой системы управления
передаточная функция разомкнутой системы управления

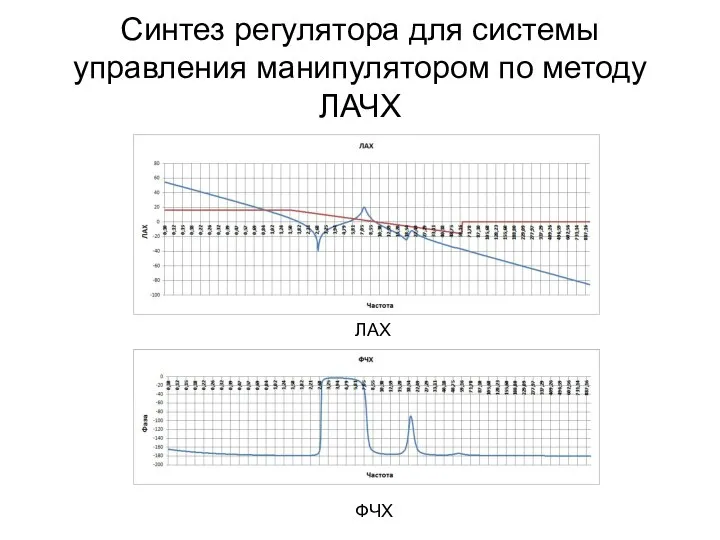
Синтез регулятора для системы управления манипулятором по методу ЛАЧХ
ЛАХ
ФЧХ

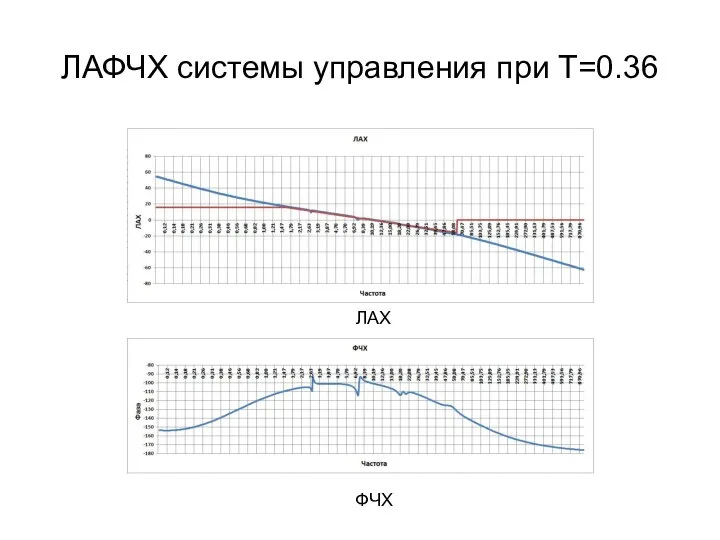
ЛАФЧХ системы управления при T=0.36
ЛАХ
ФЧХ

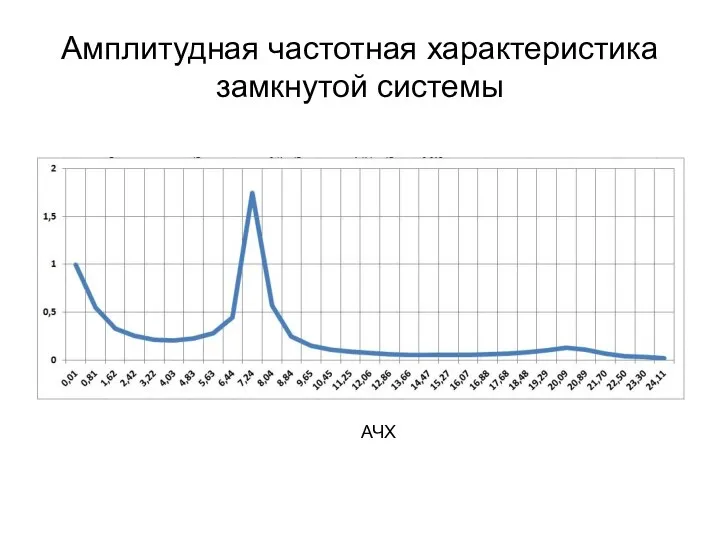
Амплитудная частотная характеристика замкнутой системы
АЧХ

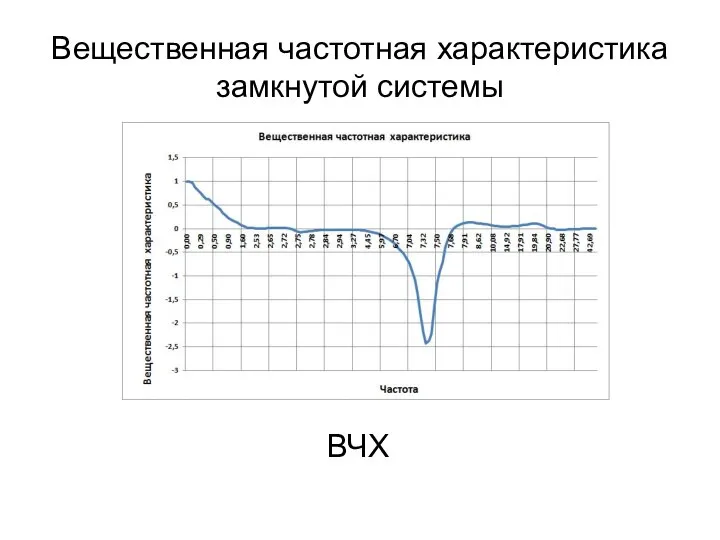
Вещественная частотная характеристика замкнутой системы
ВЧХ

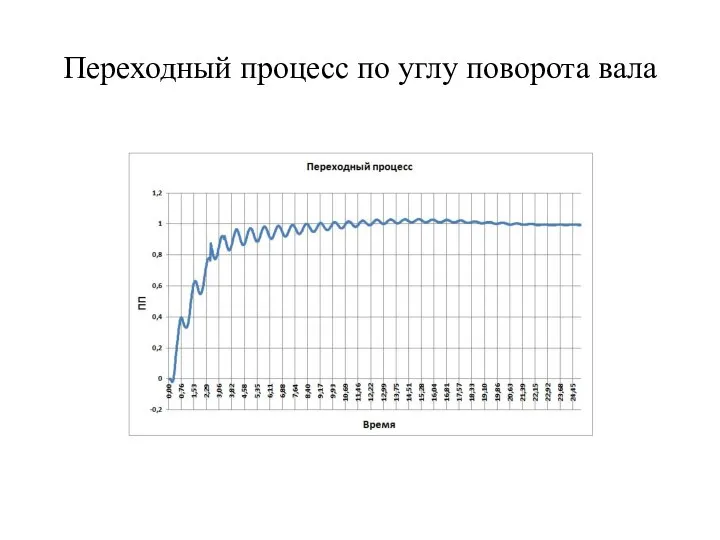
Переходный процесс по углу поворота вала

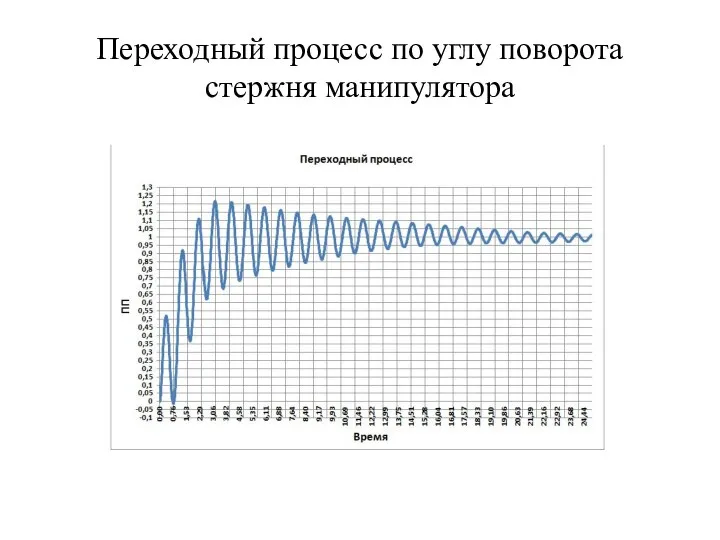
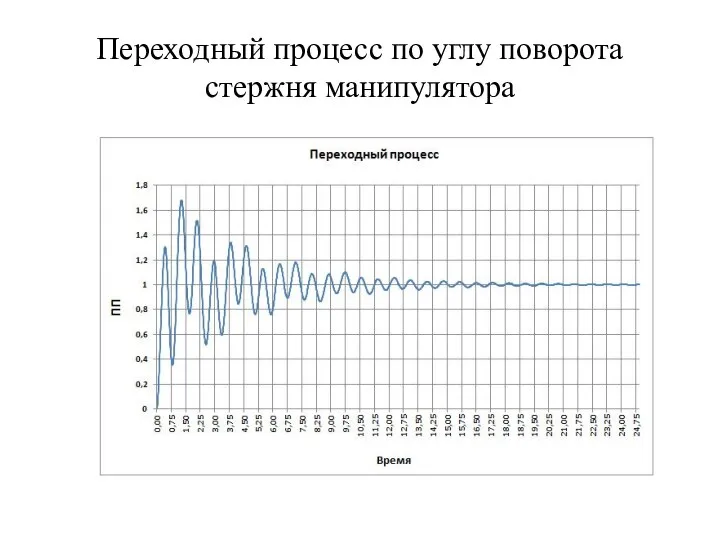
Переходный процесс по углу поворота стержня манипулятора

Исследование устойчивости системы управления манипулятором по критерию Михайлова

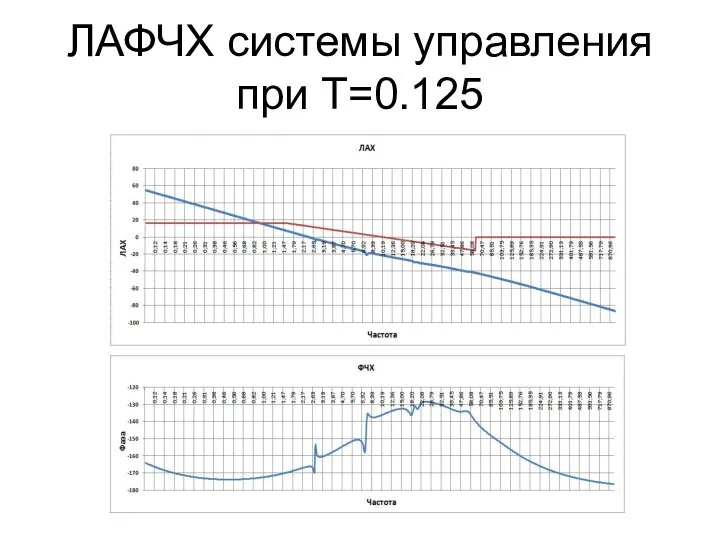
ЛАФЧХ системы управления при T=0.125

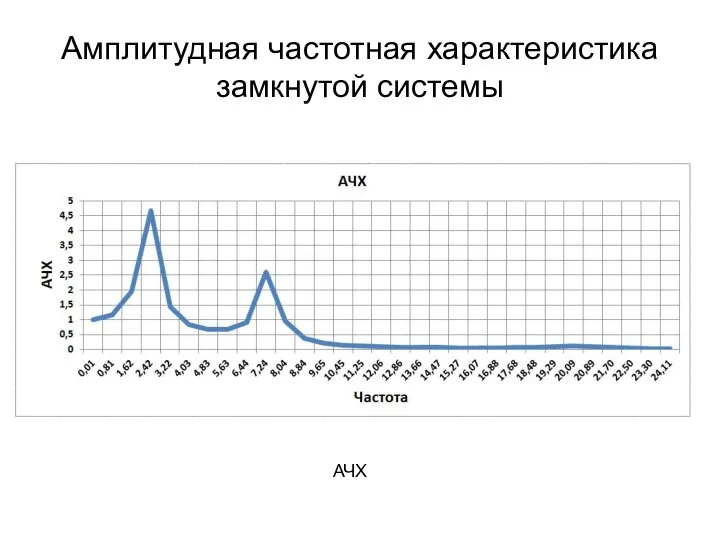
Амплитудная частотная характеристика замкнутой системы
АЧХ

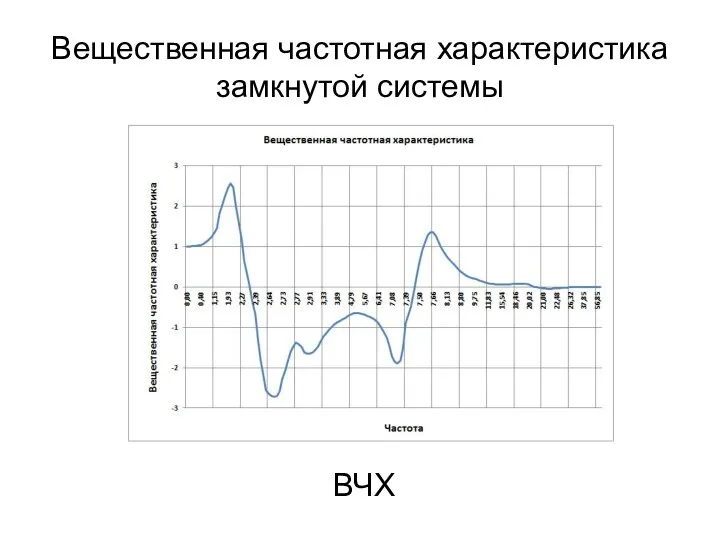
Вещественная частотная характеристика замкнутой системы
ВЧХ

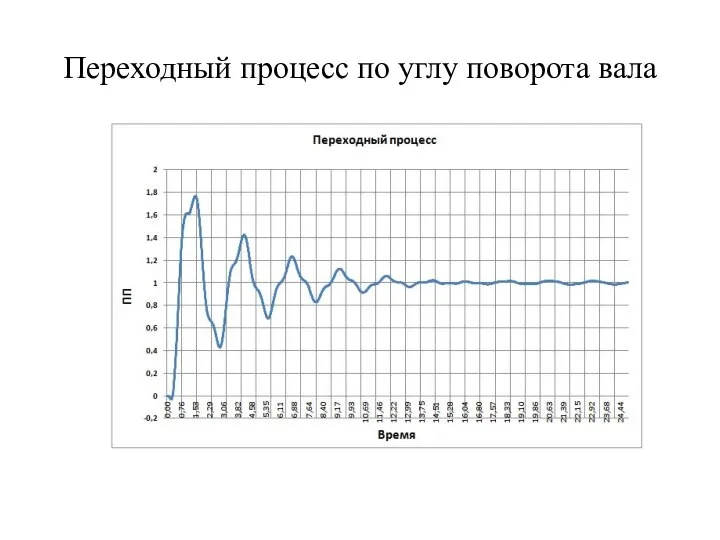
Переходный процесс по углу поворота вала

Переходный процесс по углу поворота стержня манипулятора

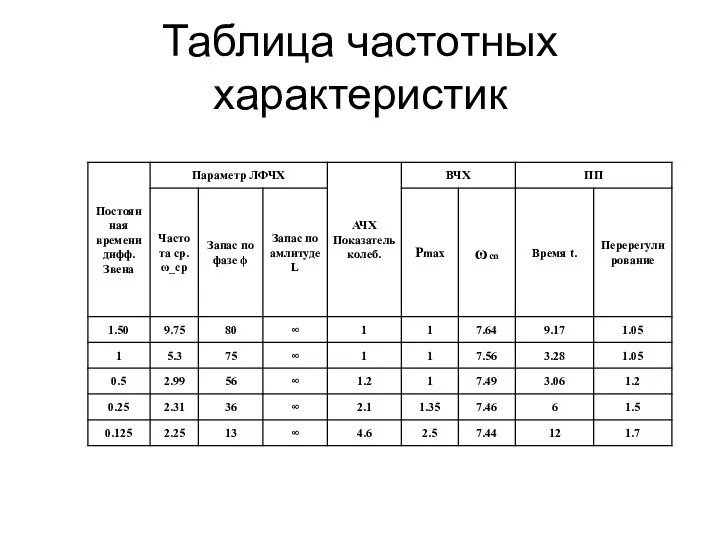
Таблица частотных характеристик

ЗАКЛЮЧЕНИЕ
СФОРМУЛИРУЕМ ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ ПО ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЕ:
1. Разработаны размерная и безразмерная математические модели системы управления манипулятора с рабочим инструментом в виде вязкоупругого стержня.
2. Сформирована структурная схема системы управления плоским движением манипулятора с вязкоупругим стержнем. Получены передаточные функции разомкнутой и замкнутой систем управления манипулятором.
3. Методом логарифмических амплитудных и фазовых частотных характеристик получены корректирующие устройства для системы управления плоским движением манипулятора с вязкоупругим стержнем, для разных значений частотных показателей качества управления.
4. Показано, что для системы управления манипулятора с рабочим инструментом в виде вязкоупругого стержня для получения приемлемых показателей переходных процессов требуются более высокие частотные показатели качеств по сравнению с системами с сосредоточенными параметрами.