Содержание
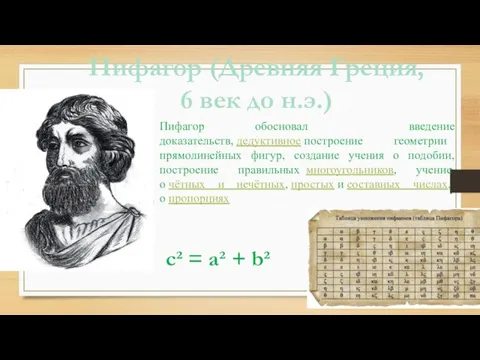
- 2. Пифагор (Древняя Греция, 6 век до н.э.) Пифагор обосновал введение доказательств, дедуктивное построение геометрии прямолинейных фигур,
- 3. Архимед (Древняя Греция, Третий век до н.э.) Архимед обосновал механику и гидростатику. Определил законы рычага и
- 4. Эратосфен – древнегреческий ученый, 3 век до н.э.) Эратосфен первым вычислил размеры земного шара. Для этого
- 5. Эвклид – математик Древней Греции (3 - 4 век до н.э.) Эвклид — первый математик Александрийской
- 6. Пьер Ферма (Франция, 17 век) Ферма ввел в аналитическую геометрию бесконечно малые величины, нашел способы нахождения
- 7. Франсуа Виет (Франция, 16 век) Виет разработал основы элементарной алгебры. Он первым стал обозначать буквами не
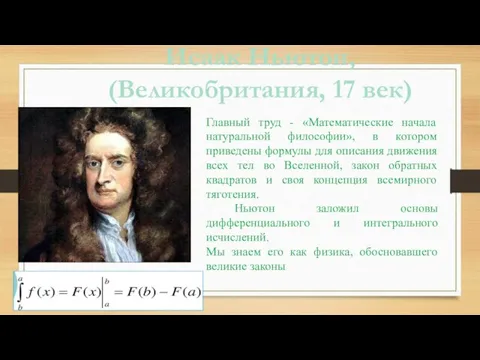
- 8. Исаак Ньютон, (Великобритания, 17 век) Главный труд - «Математические начала натуральной философии», в котором приведены формулы
- 9. В 1703 Магницкий разработал рукописный курс по геометрии, тригонометрии и кораблевождению и выпустил в свет первый
- 10. Лобачевский Николай Иванович, Россия,19 век) Фундаментальный труд - «О началах геометрии». Николай Иванович Лобачевский описал уточнённое
- 11. Софья Васильевна Ковалевская (Россия, 19 век) Обосновала теорию вращения твёрдого тела. Открыла третий случай разрешимости задачи
- 12. Мстислав Келдыш (СССР, двадцатый век) Внес свой вклад в теорию функций, теорию потенциала, дифференциальные уравнения, функциональный
- 13. Русский математик, один из создателей дескриптивной теории функций, автор ряда мировых математических открытий, оказавших определяющее влияние
- 14. Понтрягин Лев Семенович (СССР, двадцатый век) Лев Семенович внес значительный вклад в алгебраическую и дифференциальную топологию,
- 16. Скачать презентацию











 Решение задач
Решение задач Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Основы логики
Основы логики Гамильтоновы цепи в некоторых типах линейно-выпуклых графов
Гамильтоновы цепи в некоторых типах линейно-выпуклых графов Интересные факты в тригонометрии
Интересные факты в тригонометрии Тест Смешанные числа
Тест Смешанные числа Треугольник и его виды
Треугольник и его виды Применение математики в банковском деле
Применение математики в банковском деле Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Каков развивающий потенциал функциональной линии в курсе математики?
Каков развивающий потенциал функциональной линии в курсе математики? Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ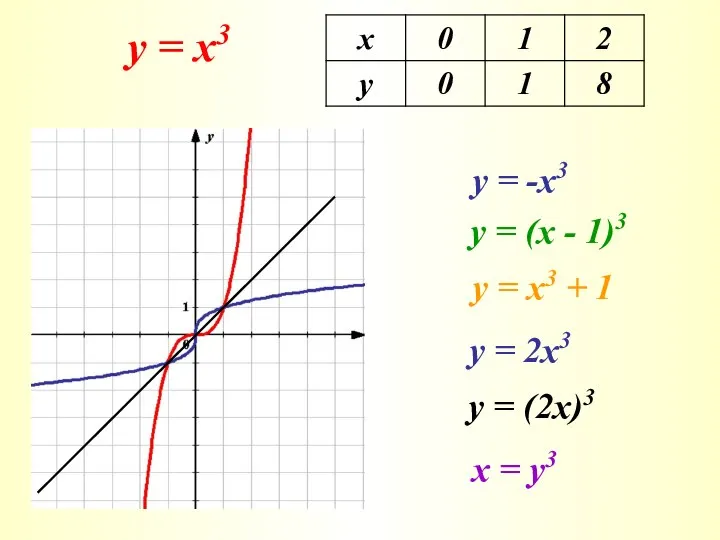 Логарифмические функции
Логарифмические функции Многоугольники в жизни
Многоугольники в жизни Алгебра в нашей жизни
Алгебра в нашей жизни Багдадская математическая школа
Багдадская математическая школа Основы теории графов
Основы теории графов Презентация на тему Свойства степени с рациональным показателем
Презентация на тему Свойства степени с рациональным показателем  Тригонометрические функции
Тригонометрические функции Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Деление с остатком
Деление с остатком Решение примеров
Решение примеров Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Решение неравенств с одной переменной. 8 класс
Решение неравенств с одной переменной. 8 класс Параллельный перенос
Параллельный перенос Подготовка к контрольной работе
Подготовка к контрольной работе Линейные уравнения. Ярмарка по решению старинных русских задач
Линейные уравнения. Ярмарка по решению старинных русских задач Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений