Содержание
- 2. Ответ: 10101. (Самопроверка.) Поставьте себе оценку: «5» - за 5 верно выполненных заданий; «4» - за
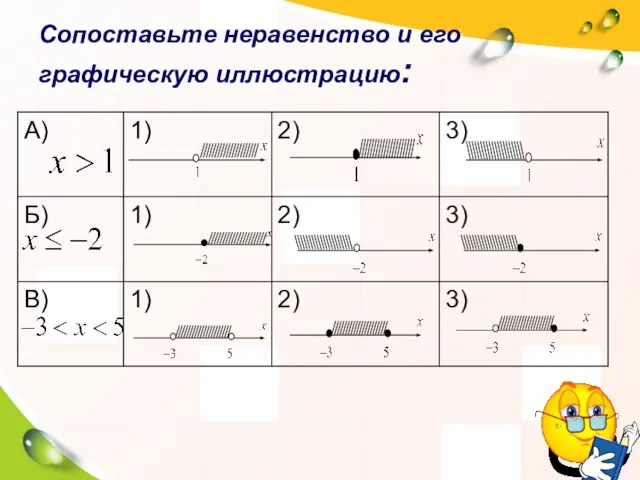
- 3. Сопоставьте неравенство и его графическую иллюстрацию:
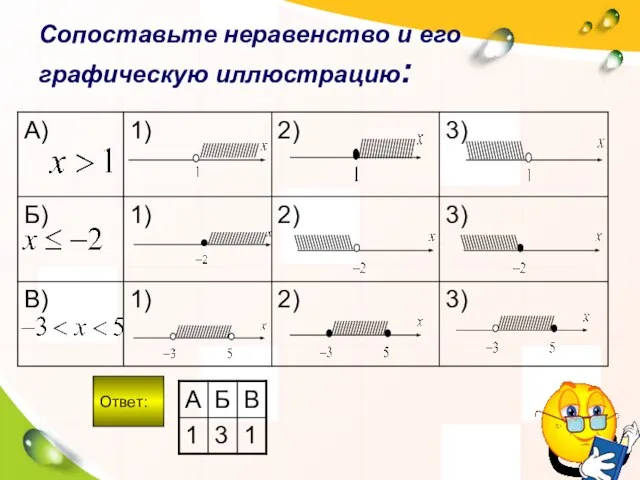
- 4. Сопоставьте неравенство и его графическую иллюстрацию: Ответ:
- 5. «Лови ошибку!» Решить неравенства: №1 3х - 3 3х – х 2х х > 3,5 -
- 6. «Лови ошибку!» Решить неравенства: №1 3х - 3 3х – х 2х х Ответ: (-∞; 3,5)
- 7. Решить неравенство: (x - 4)2 (x+4)(x-4) х2 – 8х + 16 – х2 – 8х х
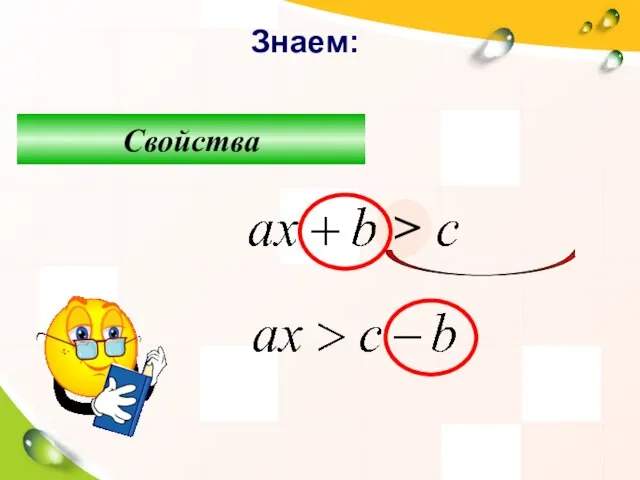
- 8. Знаем: Свойства ≥ ≤ >
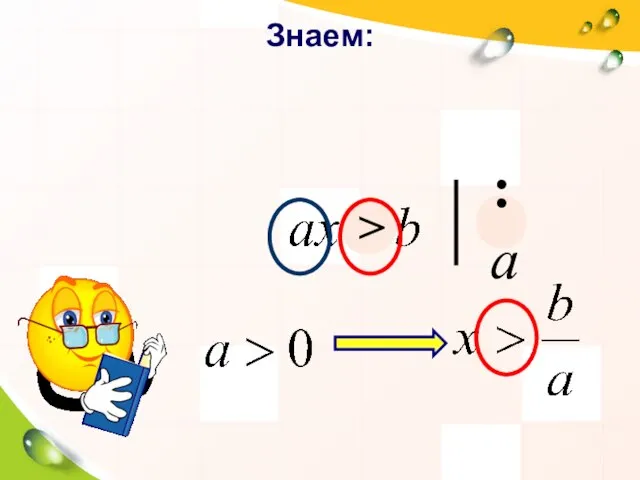
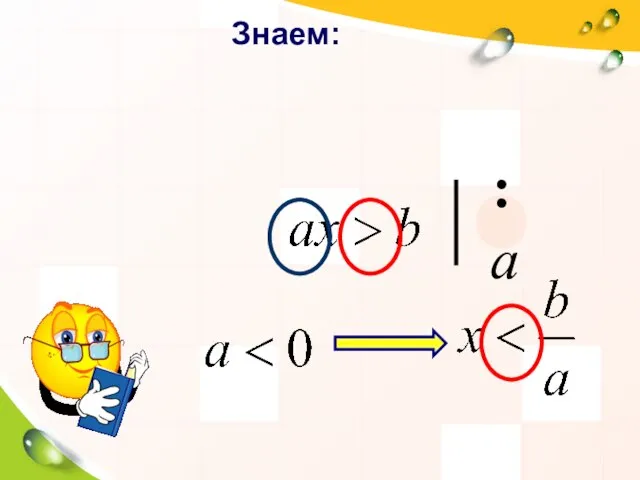
- 9. Знаем: ≥ ≤ > :а
- 10. Знаем: :а
- 11. Изучение новой темы.
- 12. Что назовем решением системы? Решением системы неравенств с одной переменной называется значение переменной, при котором верно
- 13. Алгоритм решения систем неравенств Чтобы решить систему неравенств, надо: 1) решить каждое неравенство системы; 2) Изобразить
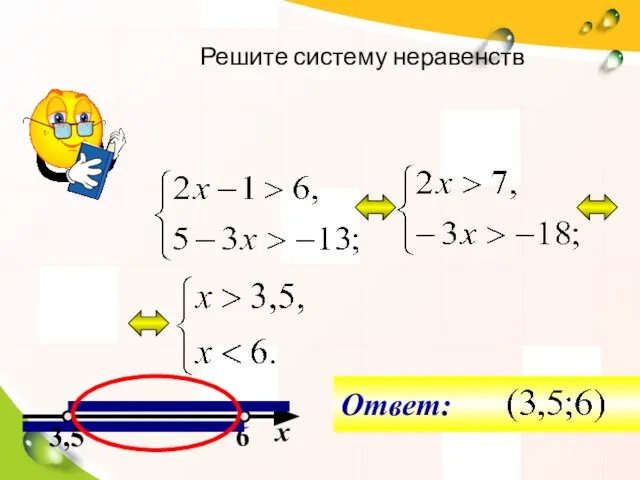
- 14. 6 3,5 х Решите систему неравенств
- 15. Рефлексия: Оцените свою работу: 5б- всё понял и могу рассказать. 4б-всё понял, но рассказать не могу.
- 17. Скачать презентацию








 Смешанные числа (часть 1)
Смешанные числа (часть 1) Нахождение процентов от числа
Нахождение процентов от числа Параллелограмм
Параллелограмм Комплéксные числа. Лекция 2
Комплéксные числа. Лекция 2 Арифметичская прогрессия
Арифметичская прогрессия Доли. Математический диктант
Доли. Математический диктант Виды треугольников
Виды треугольников Площадь треугольника
Площадь треугольника Прямоугольный треугольник
Прямоугольный треугольник Кадры, производительность труда, заработная плата
Кадры, производительность труда, заработная плата Решение примеров в пределах 10
Решение примеров в пределах 10 Конус. Площадь поверхности конуса
Конус. Площадь поверхности конуса Производные и первообразные 1
Производные и первообразные 1 Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Применение производной в географии. 10 класса
Применение производной в географии. 10 класса Математические ребусы. 2 класс
Математические ребусы. 2 класс Упрощение выражений. Тест
Упрощение выражений. Тест Нелинейное программирование
Нелинейное программирование Решаем задачу
Решаем задачу Квест-игра по математике
Квест-игра по математике Решение системы линейных уравнений. Методы решения системы линейных уравнений
Решение системы линейных уравнений. Методы решения системы линейных уравнений Координаты вектора
Координаты вектора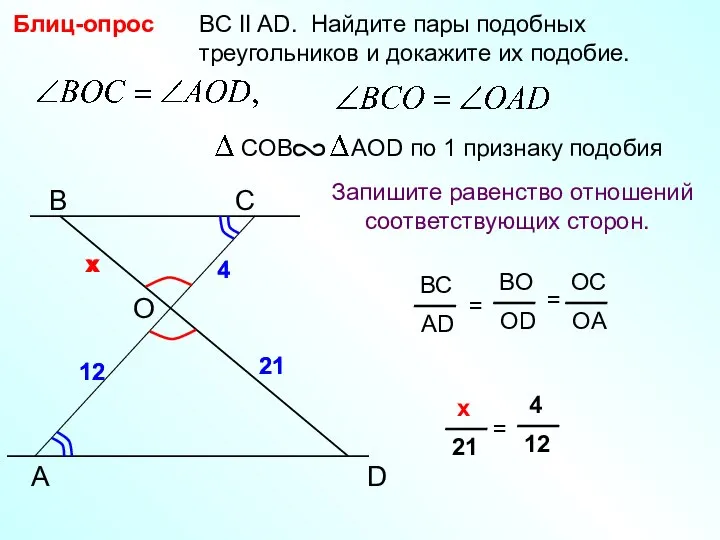 Признаки подобия треугольников
Признаки подобия треугольников Вычитание чисел. Математический тренажер
Вычитание чисел. Математический тренажер Определенный интеграл. Решение примеров на нахождение первообразных и интегралов
Определенный интеграл. Решение примеров на нахождение первообразных и интегралов Таблица Шульте
Таблица Шульте Изучение геометрического материала по программе Л.Г. Петерсон Школа 2000
Изучение геометрического материала по программе Л.Г. Петерсон Школа 2000