Рекуррентныя уравнения

Понятие
Для некоторой задачи под подзадачей мы будем понимать:
- ту же задачу, но меньшим числом параметров,
или
- задачу с тем же числом параметров, но при этом хотя бы один из параметров имеет меньшее значение.

Рекуррентное уравнение
соотношения, связывающие одни и те же функции, но с различными аргументами, называются рекуррентными уравнениями.

Правильное рекуррентное уравнение
Рекуррентное уравнение называется правильным если значения аргументов у любой из функций правой части соотношения меньше значения аргументов любой из функций левой части соотношения; если аргументов несколько, то достаточно уменьшение одного из них.
Правильное рекуррентное уравнение называется полным, если оно определено для всех допустимых значений аргументов.

Примеры
T(n) = T(n - 1) + T(n - 2)
T(n) = F(n - 2) + T(n - 1)
T(n) = T(n - 1) + T(n + 1)
T(i) = T(i-1) + ai , i > 1; T(1) = a1

Примеры рекуррентных уравнений
1. Нахождение максимального элемента из n элементов массива
T(n) = T(n-1) + C= (T(n - 2) + C) + C = · · · =
=C · (n - 1), T(1) = 0, где C = O(1)
2. Нахождение наибольшего и наименьшего из n элементов массива
T(n) = 1, при n = 2;
T(n) = 2T(n/2) + 2, при n > 2.

Решение рекуррентных уравнений
Метод итераций
Подстановочный метод
Метод рекурсивных деревьев

Метод итераций
Метод заключается в том, что данное рекуррентное уравнение расписывается через множество других и затем происходит суммирование полученного выражения.

Пример 1
Найти методом итераций решение для рекуррентного уравнения:
T(n) = 2T(n/2) + 5n2
T(1) = 7

Решение
Для простоты мы предположим, что n является степенью 2 , т.е. n = 2к
T(n) = 2T(n/2) + 5n2 =
= 2(2T (n/4) + 5 (n/2)2 ) + 5n2 =
= 2(2(2T (n/8) + 5 (n/4)2 ) + 5 (n/2)2 ) + 5n2 =…=
=2к T(1) + 2к-1 · 5 (n/2k-1 ) 2 + … + 2 · 5 (n/2)2 + 5n2

Решение

Пример 2
Найти методом итераций решение для рекуррентного уравнения:
T(n) = aT(n-1) + bn,
0< a < 1, n >1, T(1) = 0

Решение

Подстановочный метод
Метод заключается в том, что методом подбора находится такая функция g(n), при подстановке которой в рекуррентное уравнение вместо T(n) получается верное неравенство в котором
g(n)=Левая часть ≥ правой части
! Функция должна быть наименьшего возможного порядка.

Пример
Предположим, что необходимо решить следующее рекуррентное уравнение
T(n) = 2T(n/2) + n
g(n) ≥ 2g(n/2) + n
g(n)=cn
g(n)=cn2
g(n)=cnlog2n

Пример
Предположим, что необходимо решить следующее рекуррентное уравнение
T(n) = 2T(n/2) + b
g(n) ≥ 2g(n/2) + b
g(n)=cn
g(n)=cn2
g(n)=c1n+c2

Метод рекурсивных деревьев
На первой итерации формируется дерево следующего вида:
- в корень дерева заносится свободный член исходного рекуррентного уравнения,
- сыновьями этого корня являются рекуррентные функции правой части исходного соотношения.
На последующих итерациях для каждого из сыновей строится аналогичная древовидная структура.

Метод рекурсивных деревьев
3. Процесс построения древовидной структуры заканчивается, когда все значения висячих вершин равны Т(1)
- при этом значения внутренних вершин дерева есть некоторые явные функции (не рекуррентные) от размера задачи;
- висячие вершины построенной древовидной структуры не обязательно одинаково удалены от корня.

Метод рекурсивных деревьев
4. После построения дерева суммирование значений в вершинах производится следующим образом:
1. Определяются суммы значений для равноудаленных от корня вершин (эти вершины находятся на одном уровне),
2. Находится максимальная сумма по уровням. 3. Общая трудоемкость алгоритма ограничена сверху одним из следующих значений:
a) максимальной суммой, умноженной на количество уровней,
b ) суммой, полученной в результате суммирования сумм значений по уровням

Пример
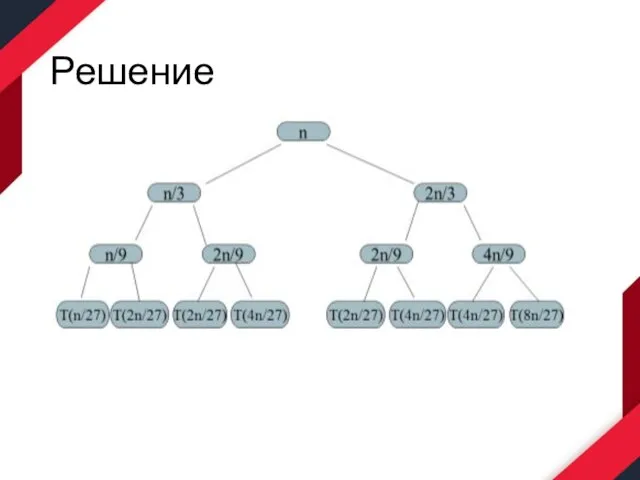
Решить следующее рекуррентное уравнение
T(n) = T(n/3)+T(2n/3)+n

Решение

Решение
- сумма на каждом уровне равна n
- количество уровней равно log3/2n
T(n) = cnlog2n

Пример
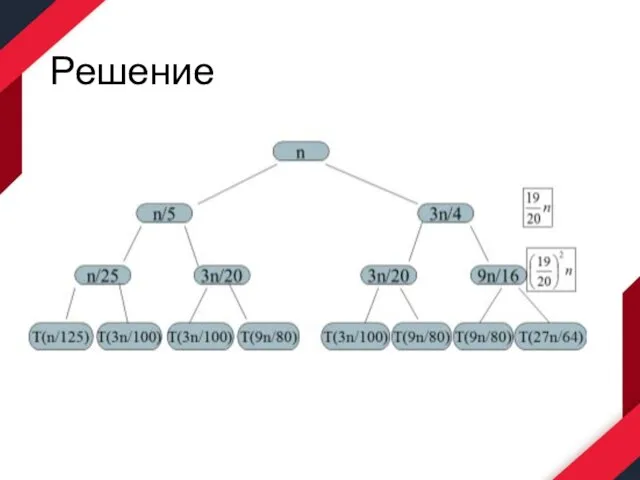
Решить следующее рекуррентное уравнение
T(n) = T(n/5)+T(3n/4)+n

Решение

Решение
T(n) = T(n/5)+T(3n/4)+n≤
≤ n(1+q+q2+q3+…+qlog4/3n) ≤20n
где q = 19/20.
T(n) = O(n)