Шар и сфера

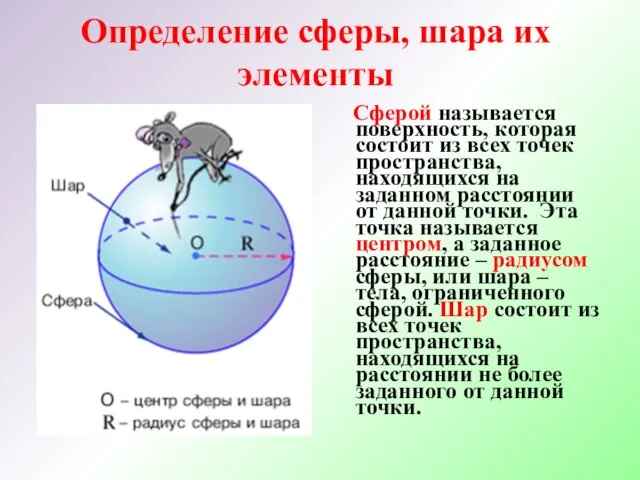
Определение сферы, шара их элементы
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

Шар и сфера – это разные геометрические тела. Однако оба слова «шар» и «сфера» происходят от одного и того же греческого слова «сфайра» - мяч. При этом слово «шар» образовалось от перехода согласных сф в ш. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы.

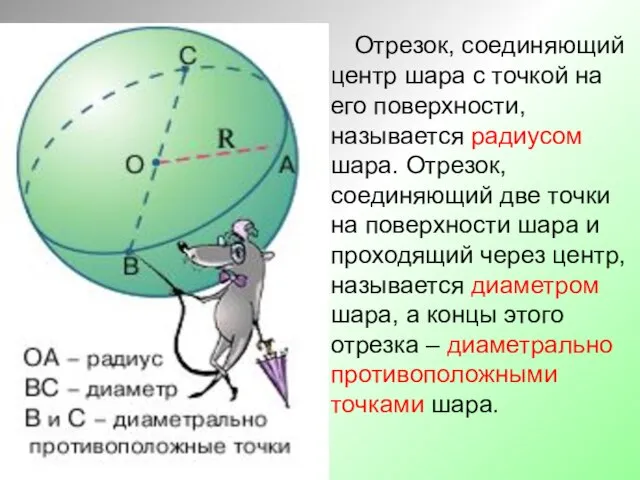
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.

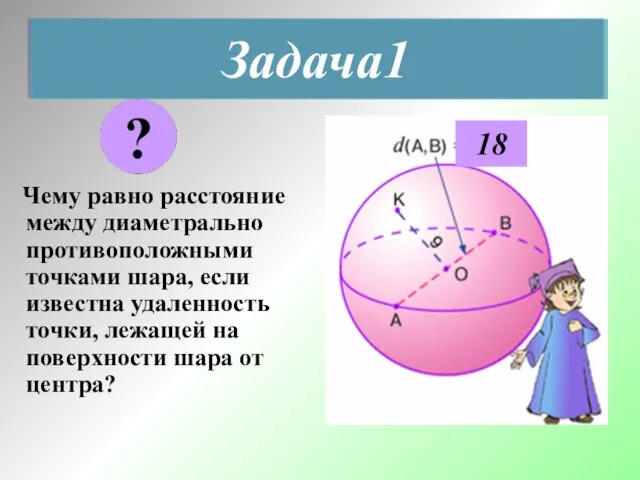
Задача1
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?
18

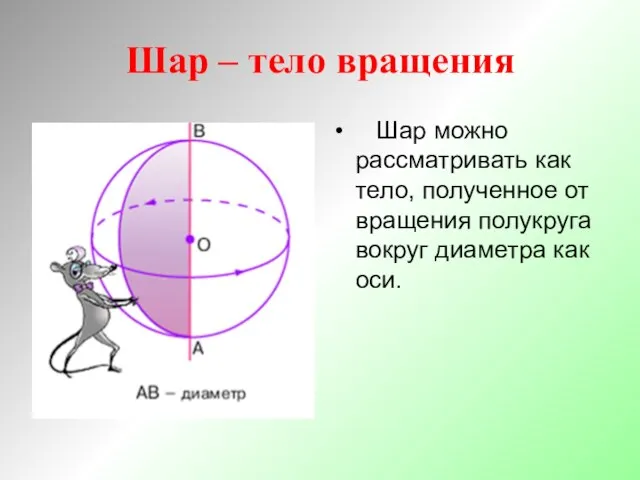
Шар – тело вращения
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

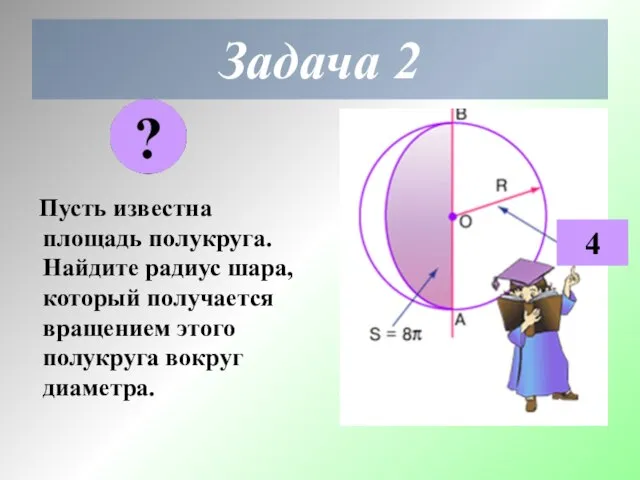
Задача 2
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.
4

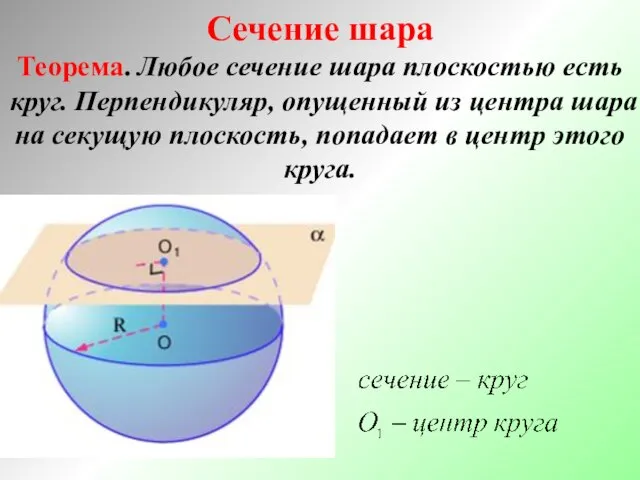
Сечение шара
Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.

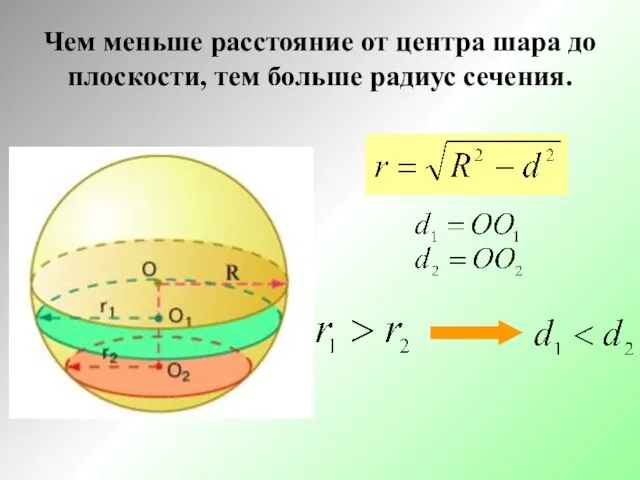
Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

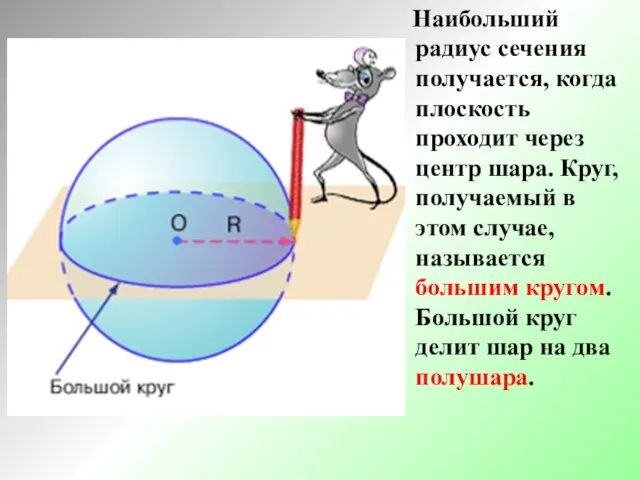
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.

Задача 3
Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.
10

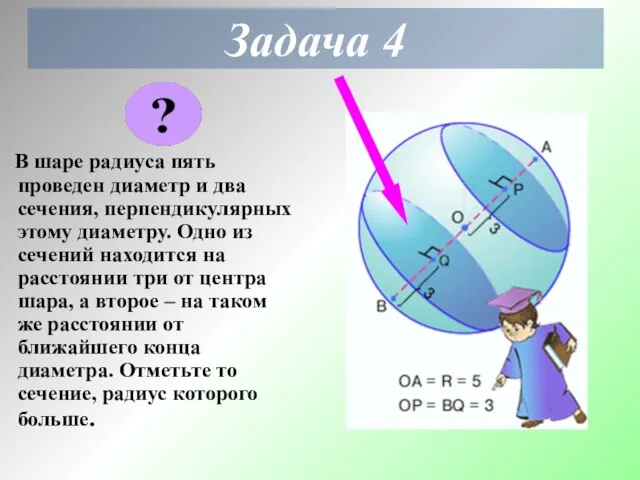
Задача 4
В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.

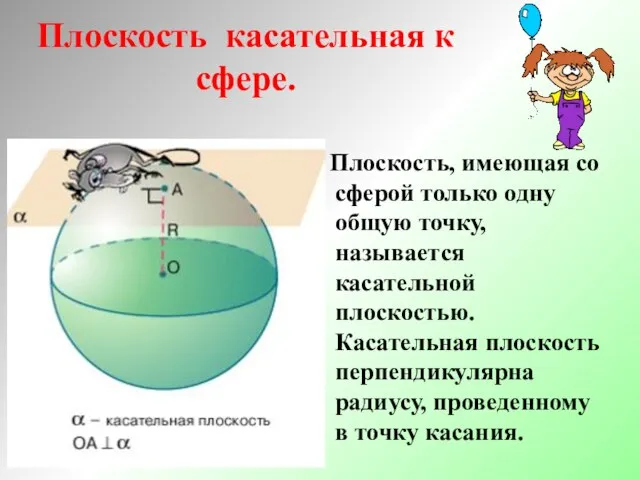
Плоскость касательная к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

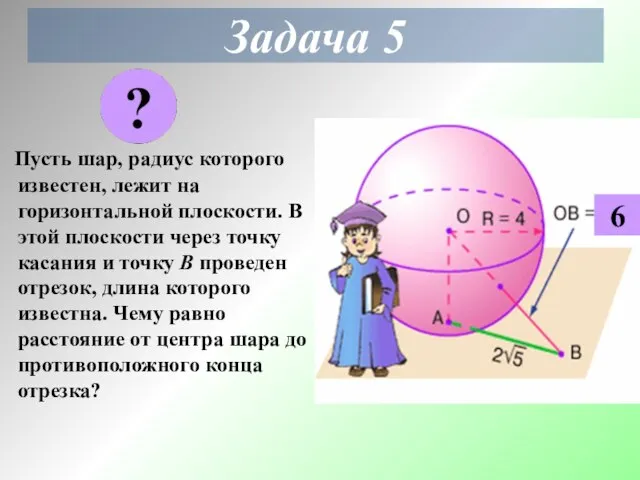
Задача 5
Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?
6

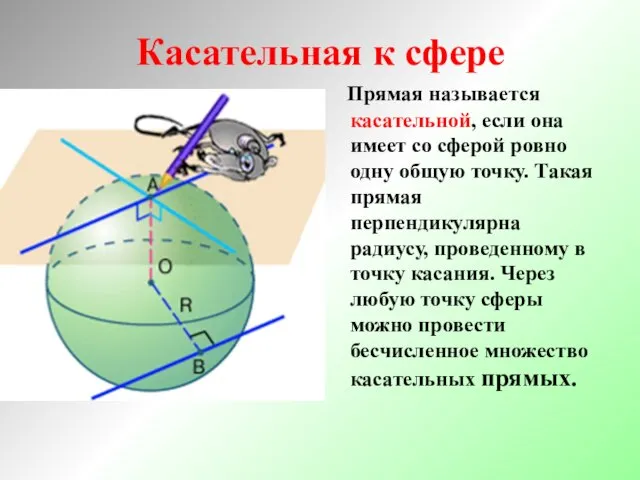
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.
Касательная к сфере

Задача 6
Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?
4

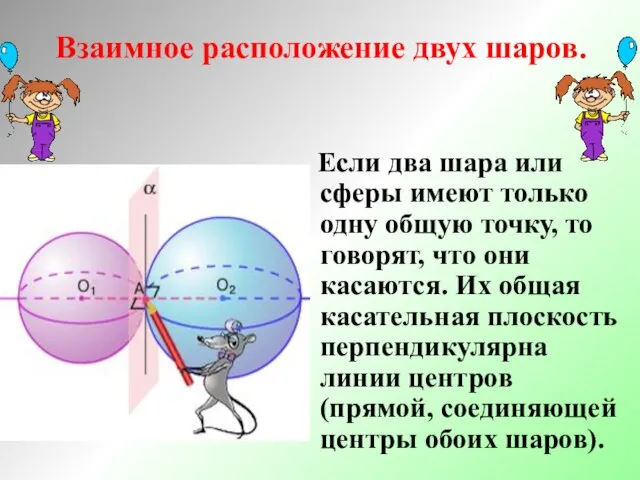
Взаимное расположение двух шаров.
Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).

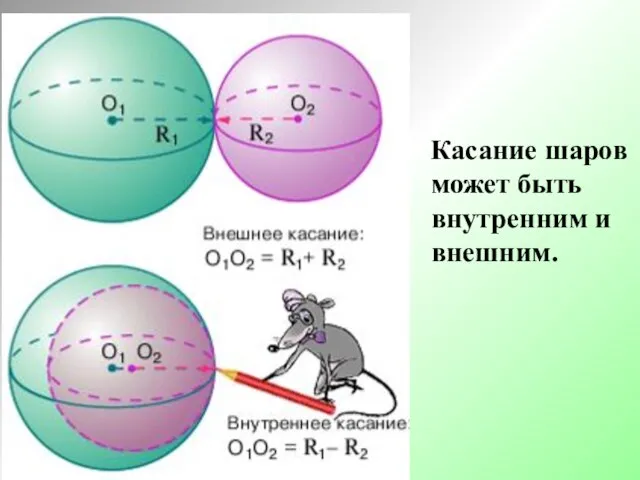
Касание шаров может быть внутренним и внешним.

Задача 7
Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.
2
8

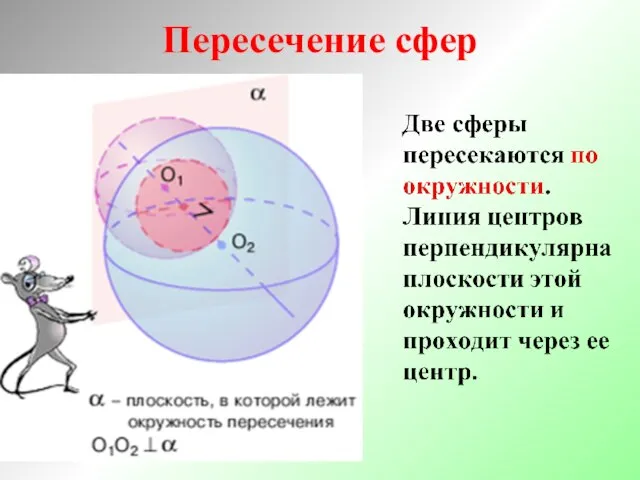
Пересечение сфер

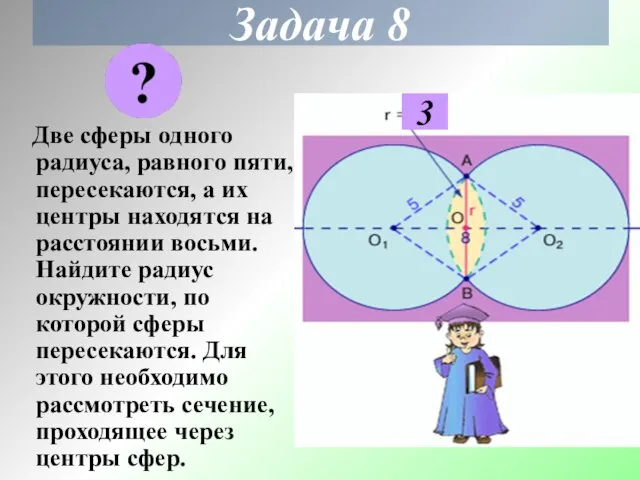
Задача 8
Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.
3

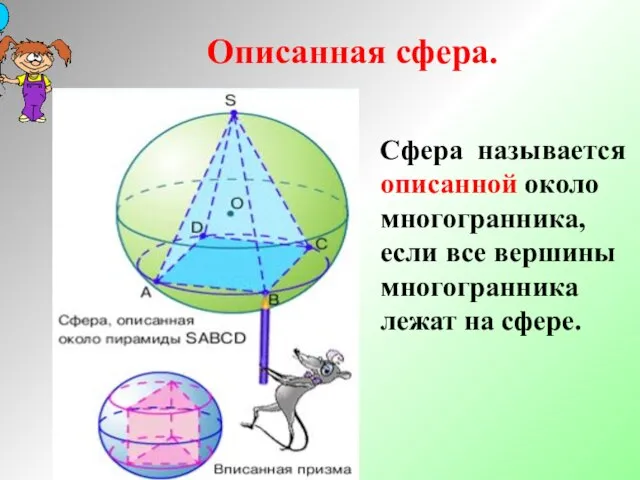
Описанная сфера.
Сфера называется описанной около многогранника, если все вершины многогранника лежат на сфере.

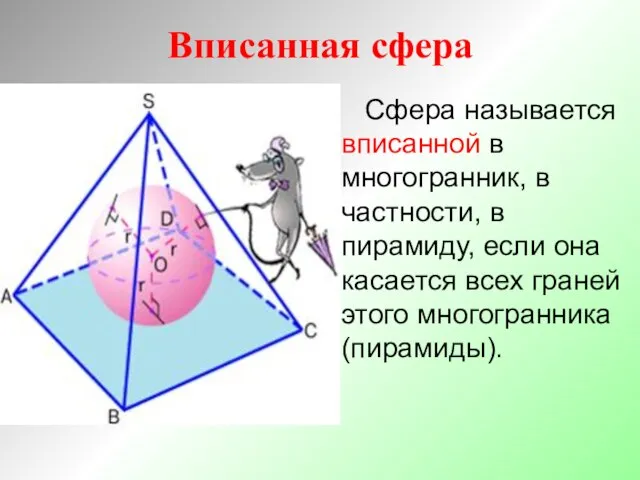
Вписанная сфера
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).

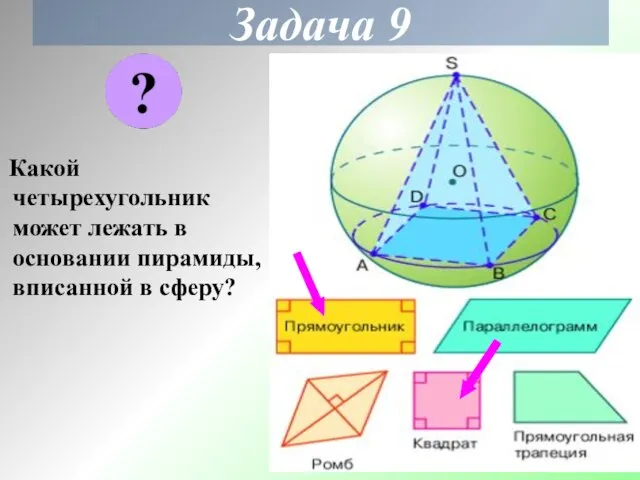
Задача 9
Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?

ИТОГОВЫЙ ТЕСТ:
1. Расстояние между центрами шаров R и r равно d (R>r). Какое утверждение неверно?
А) Если d > R+r, то шары общих точек не имеют.
Б) Если d = R+r, то шары касаются.
В) Если d = R-r, то шары имеют только одну общую точку.
Г) Если d < R+r, то шары имеют более одной общей точки.
2. Укажите неверное утверждение:
А) Если плоскость удалена от центра сферы на расстояние, большее радиуса, то плоскость и сфера не пересекаются.
Б) Если плоскость удалена от центра шара на расстояние равное радиусу, то данная плоскость является касательной к шару.
В) Касательные плоскости к шару, проведенные в диаметрально противоположных точках, параллельны.
Г) Через точку вне шара можно провести не более двух касательных к данному шару.
3. Какое утверждение не верно:
А) Если центр одной сферы находится внутри другой, то эти сферы могут иметь только одну общую точку.
Б) Если центр одной сферы находится на другой сфере, то сферы могут иметь только одну общую точку.
В) Если центр одной сферы находится на другой сфере, то сферы могут пересекаться.
Г) Если центр одной сферы находится на другой сфере, то сферы всегда имеют по крайней мере одну общую точку.

4. На какой вопрос следует ответить отрицательно?
А) Верно ли, что в любую правильную треугольную призму можно вписать шар?
Б) Верно ли, что около любой правильной треугольной призмы можно вписать шар?
В) Верно ли, что в любой тетраэдр можно вписать шар?
Г) Верно ли, что около любого тетраэдра можно описать сфер?.
5. Какое утверждение ложно?
А) Если точка удалена от центра шара на расстояние, большее радиуса шара, то она не принадлежит шару.
Б) Если точка удалена от центра сферы на расстояние, большее радиуса сферы, то она не принадлежит сфере.
В) Если точка удалена от центра шара на расстояние, меньшее радиуса шара, то она не принадлежит шару.
Г) Если точка удалена от центра сферы на расстояние, меньшее радиуса сферы, то она не принадлежит сфере.

Ключ к тесту
1) В;
2) Г;
3) Г;
4) А;
5) В.
Нет ошибок: 3 балла
Одна ошибка: 2 балла
Две ошибки: 1 балл

Критерии самооценки задач

Лист самооценки