Симметрия многогранников

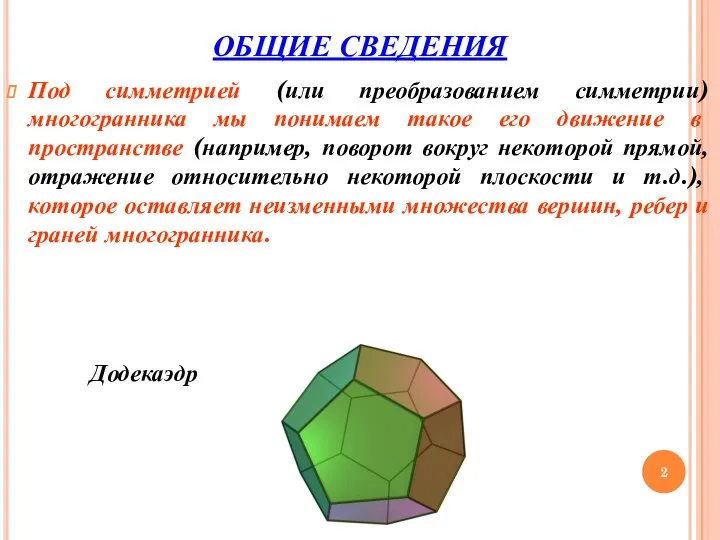
ОБЩИЕ СВЕДЕНИЯ
Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника.
Додекаэдр

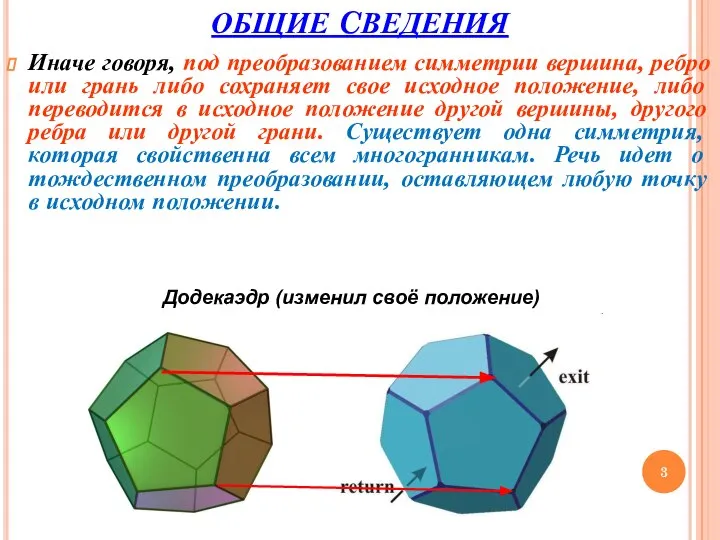
Иначе говоря, под преобразованием симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани. Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении.
ОБЩИЕ CВЕДЕНИЯ
Додекаэдр (изменил своё положение)

С самым распространенным примером симметрии мы встречаемся в случае прямой правильной n-угольной призмы. Пусть a – прямая, соединяющая центры оснований. Поворот вокруг a на любое целое кратное угла 360/n градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им.
ОБЩИЕ СВЕДЕНИЯ

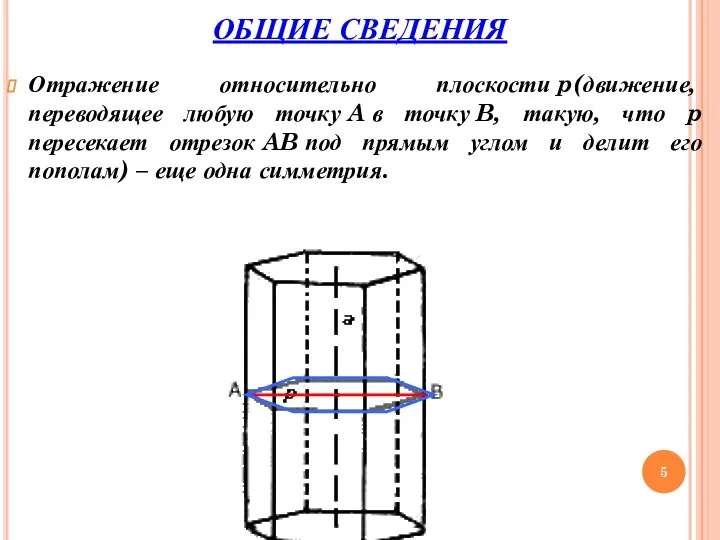
ОБЩИЕ СВЕДЕНИЯ
Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия.

ОБЩИЕ СВЕДЕНИЯ

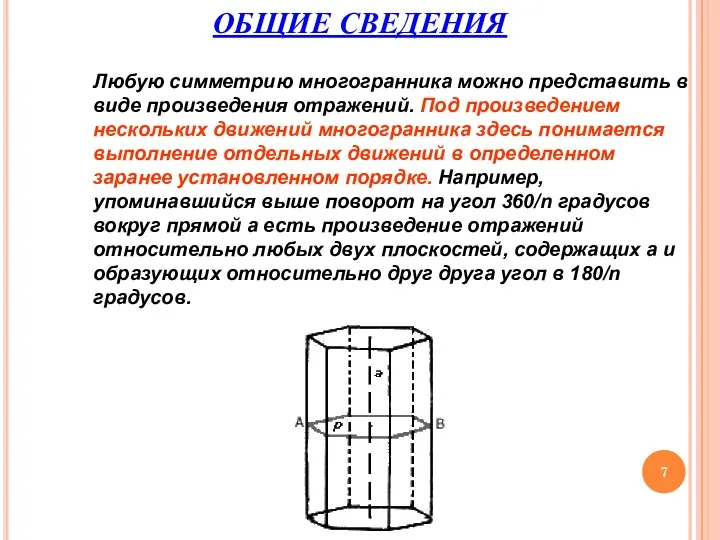
ОБЩИЕ СВЕДЕНИЯ
Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/n градусов вокруг прямой a есть произведение отражений относительно любых двух плоскостей, содержащих a и образующих относительно друг друга угол в 180/n градусов.

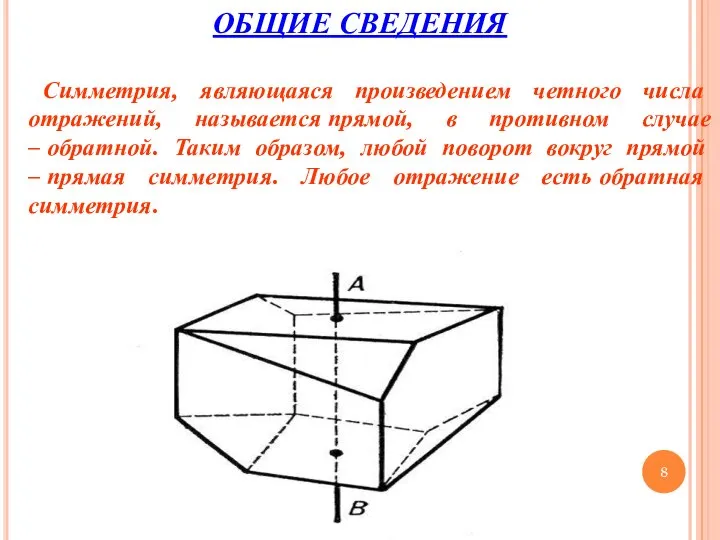
ОБЩИЕ СВЕДЕНИЯ
Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.

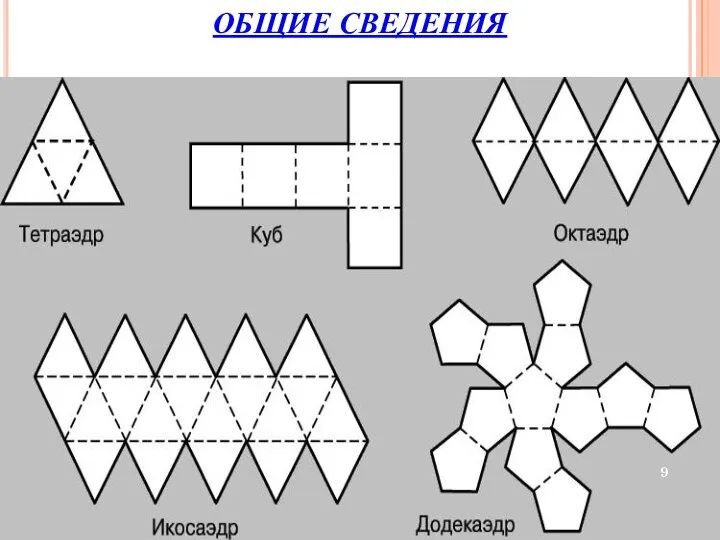
РАЗВЕРТКИ ПЯТИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ.
ОБЩИЕ СВЕДЕНИЯ

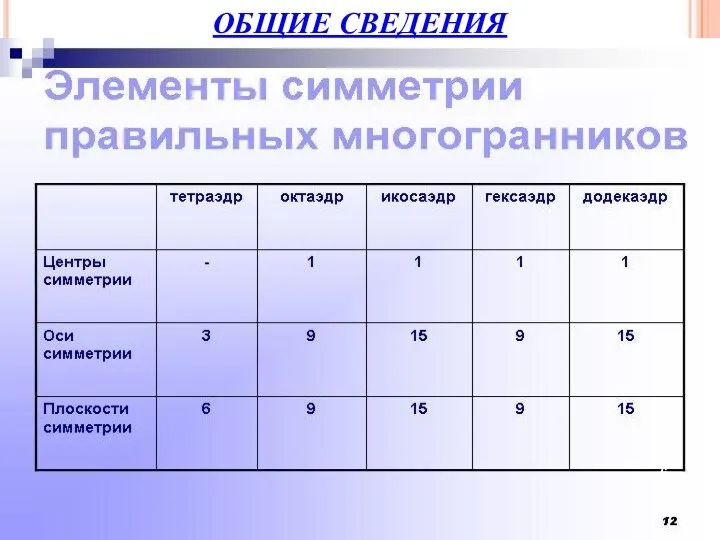
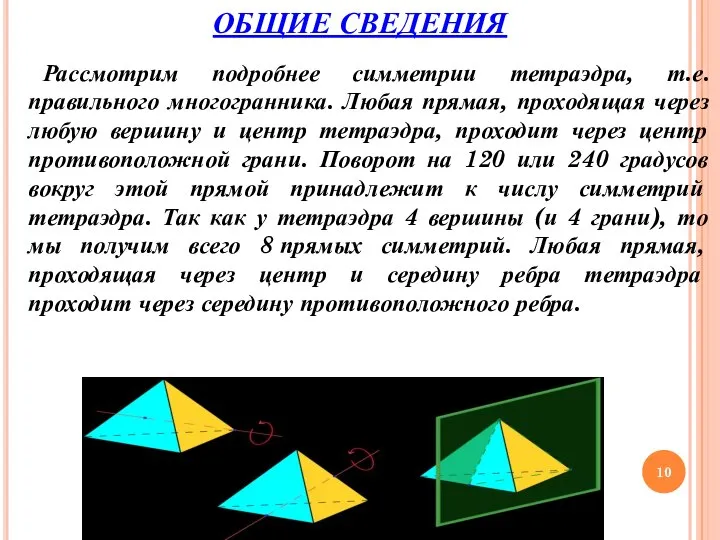
Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра.
ОБЩИЕ СВЕДЕНИЯ

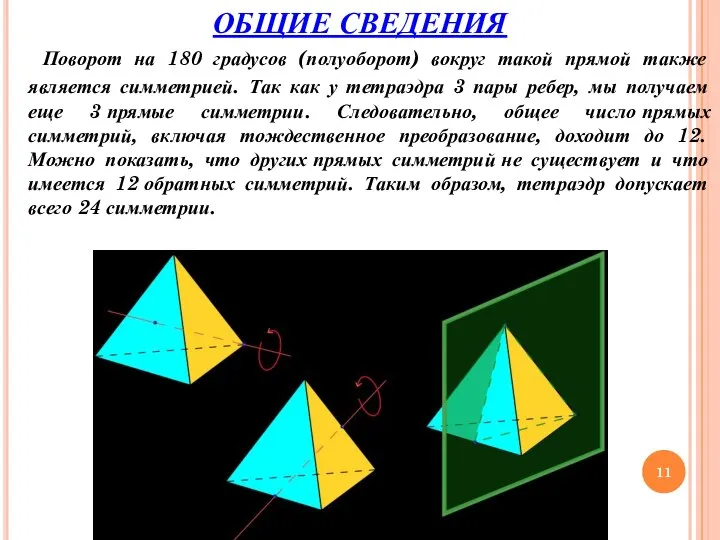
Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии.
ОБЩИЕ СВЕДЕНИЯ

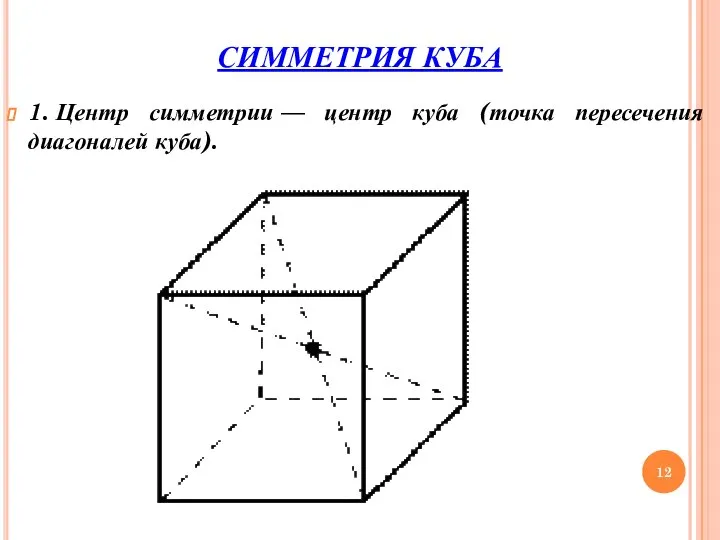
СИММЕТРИЯ КУБА
1. Центр симметрии — центр куба (точка пересечения диагоналей куба).

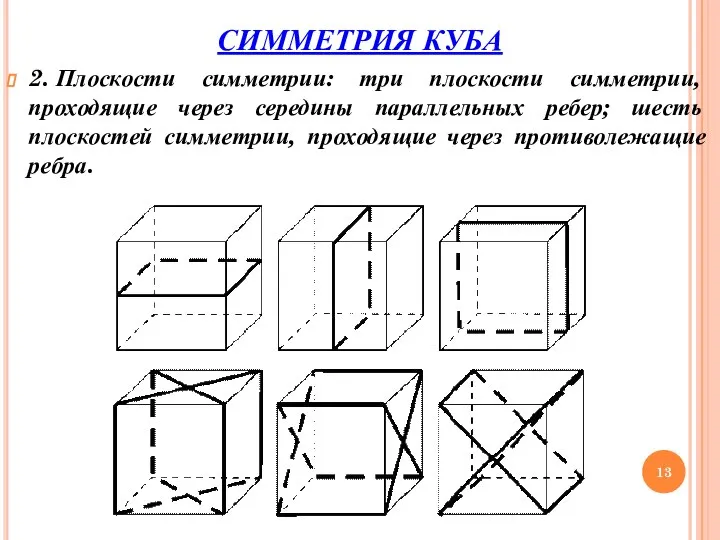
СИММЕТРИЯ КУБА
2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер; шесть плоскостей симметрии, проходящие через противолежащие ребра.

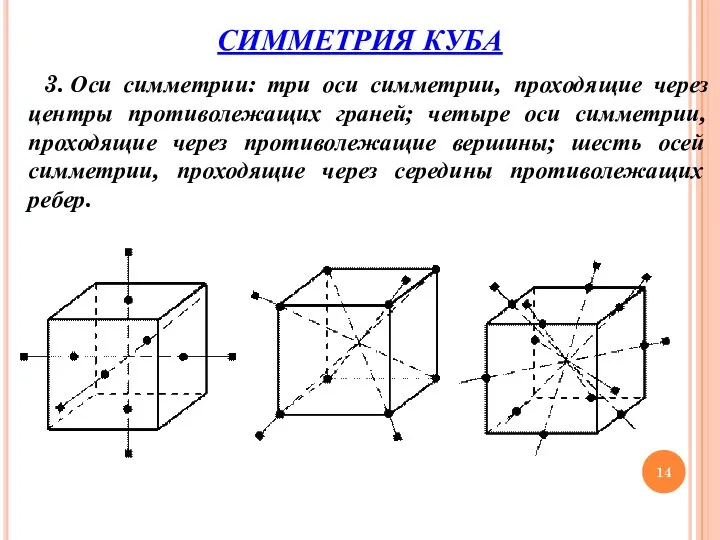
3. Оси симметрии: три оси симметрии, проходящие через центры противолежащих граней; четыре оси симметрии, проходящие через противолежащие вершины; шесть осей симметрии, проходящие через середины противолежащих ребер.
СИММЕТРИЯ КУБА

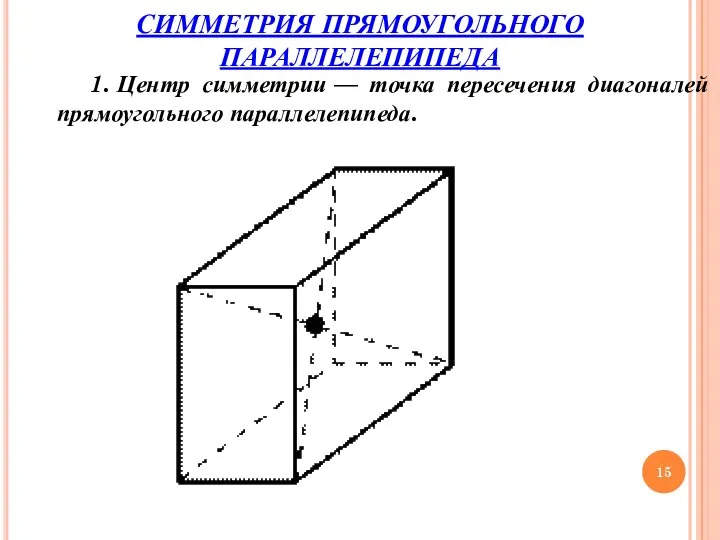
СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
1. Центр симметрии — точка пересечения диагоналей прямоугольного параллелепипеда.

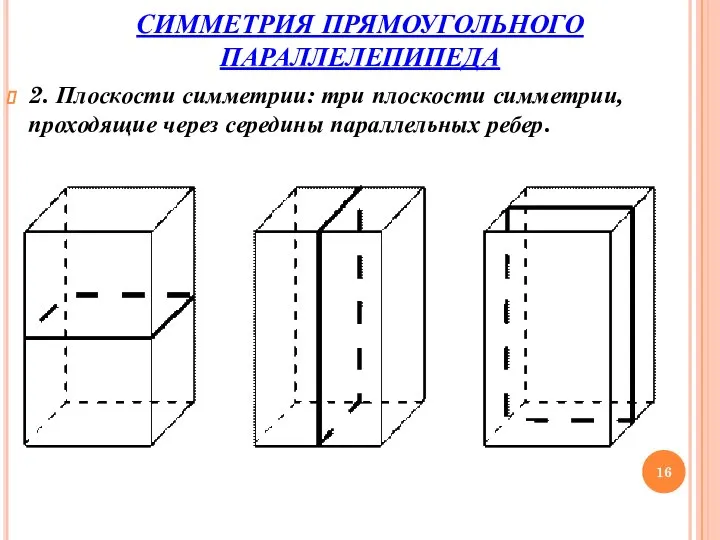
СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер.

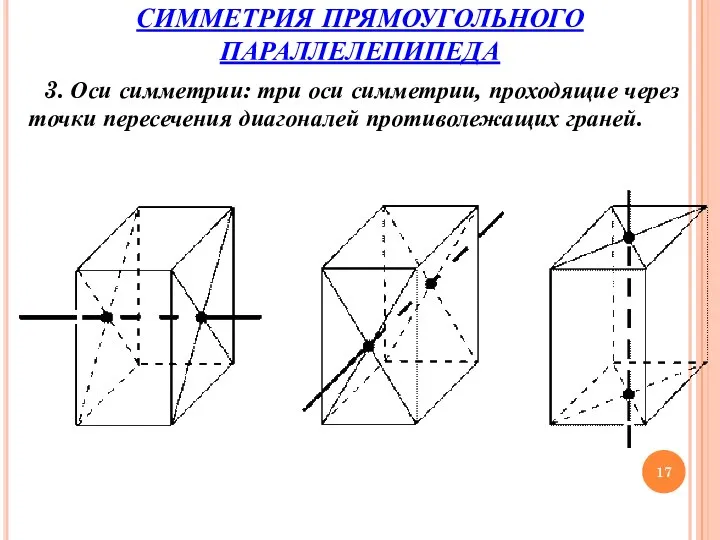
3. Оси симметрии: три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
СИММЕТРИЯ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

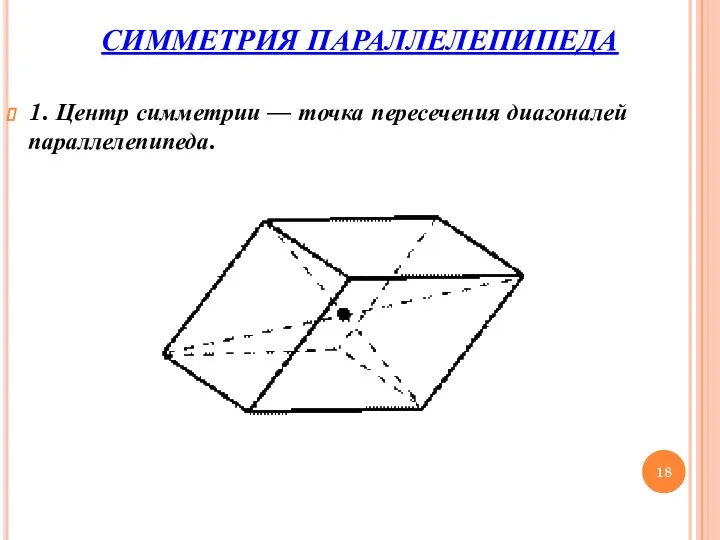
СИММЕТРИЯ ПАРАЛЛЕЛЕПИПЕДА
1. Центр симметрии — точка пересечения диагоналей параллелепипеда.

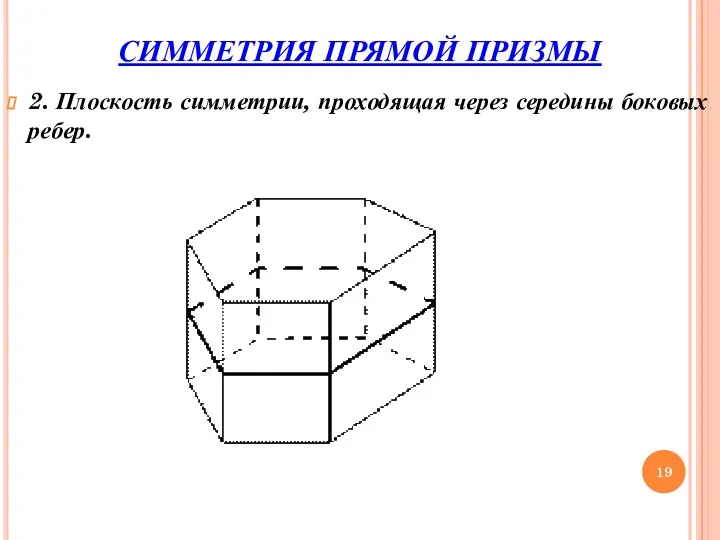
СИММЕТРИЯ ПРЯМОЙ ПРИЗМЫ
2. Плоскость симметрии, проходящая через середины боковых ребер.

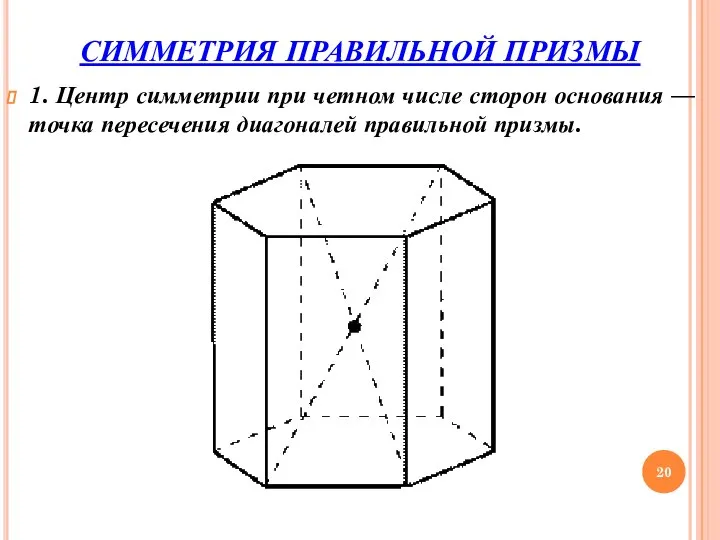
СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ
1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы.

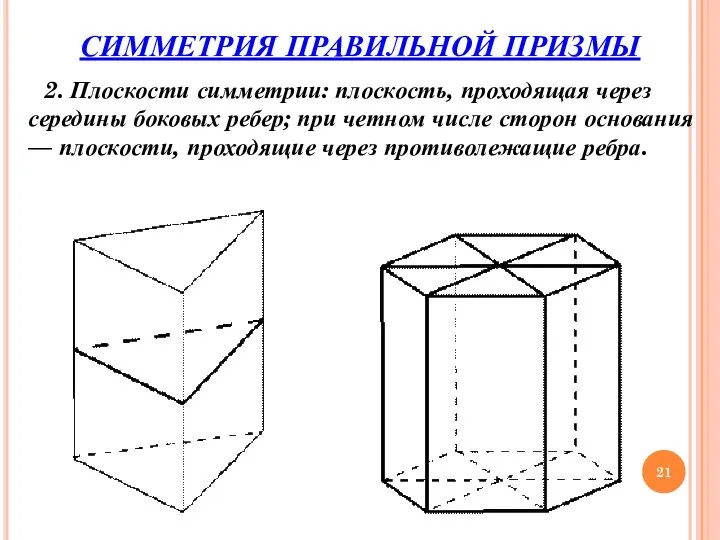
СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра.

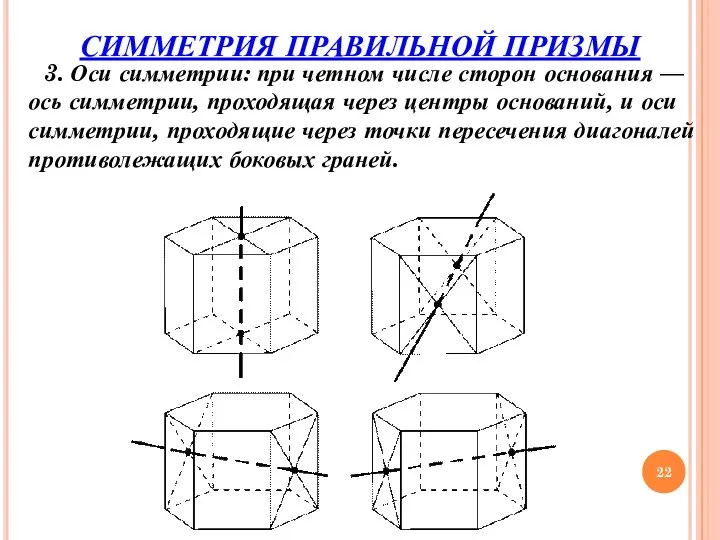
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней.
СИММЕТРИЯ ПРАВИЛЬНОЙ ПРИЗМЫ

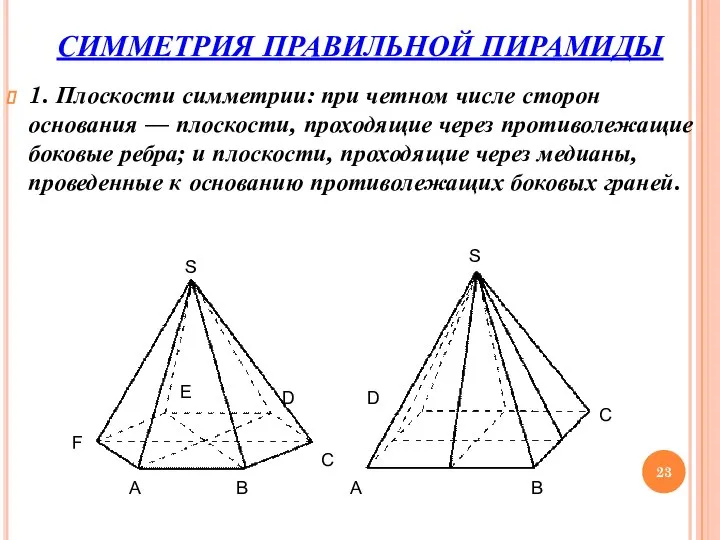
СИММЕТРИЯ ПРАВИЛЬНОЙ ПИРАМИДЫ
1. Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие боковые ребра; и плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней.
А
B
C
D
E
F
А
B
C
D
S
S