Палички Непера

Першим пристроєм для виконання множення був набір дерев’яних брусків, відомих як палички Непера. Це винахід шотландського математика Джона Непера (описаний ним у трактаті 1617 року).

Джон Непер - шотландський математик і теолог, винахідник логарифмів. Винайшов декілька корисних сільськогосподарських знарядь. У 1590-х роках дійшов ідеї логарифмічних обчислень і склав перші таблиці логарифмів, проте його знамениту працю “Опис дивовижних таблиць логарифмів” було опубліковано лише в 1614 році. Йому належить визначення логарифмів, пояснення їх властивостей, таблиці логарифмів синусів, косинусів, тангенсів і додатку логарифмів в сферичній тригонометрії. Кінематичне визначення логарифма, дане Непером, по суті, рівносильне визначенню логарифмічної функції через диференціальне рівняння. Неперу належить також ряд зручних для логарифмування формул рішення сферичних трикутників.

Палички Непера – рахунковий прилад, що складається з 10 паличок, що мали форму подовженого прямокутного паралелепіпеда. Кожна з бічних граней палички ділилася поперечними рисами на 9 квадратів, розділених, в свою чергу, проведеними в одному і тому ж напрямку діагоналями на пари трикутників. Ці квадрати містили в собі результати множення одного з перших 9 чисел в послідовному порядку від 1 до 9, причому в разі, якщо результат множення представляв двозначне число, то його десятки поміщалися в верхньому трикутнику, а одиниці в нижньому. Для подання нулів деякі з бічних поверхонь паличок залишалися не зайнятими числами.

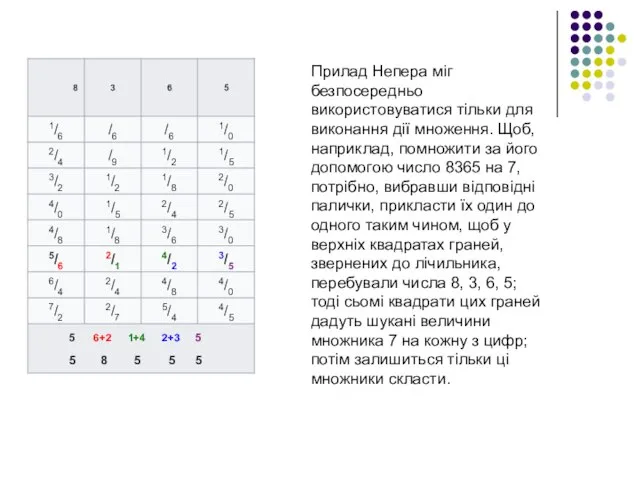
Прилад Непера міг безпосередньо використовуватися тільки для виконання дії множення. Щоб, наприклад, помножити за його допомогою число 8365 на 7, потрібно, вибравши відповідні палички, прикласти їх один до одного таким чином, щоб у верхніх квадратах граней, звернених до лічильника, перебували числа 8, 3, 6, 5; тоді сьомі квадрати цих граней дадуть шукані величини множника 7 на кожну з цифр; потім залишиться тільки ці множники скласти.