Слайд 2Основные определения
Определение
1. Тождественно равные выражения-это значения двух выражений, содержащих одни и

те же переменные, совпадают при всех допустимых значениях переменных.
2. Тождеством-равенство, верное при всех допустимых значениях, входящих в него переменных.
3. Областью допустимых значений (ОДЗ) уравнений, неравенств и их систем-это совокупность всех значений входящих в них переменных, при которых они имеют смысл
Слайд 3Рациональное уравнение и пример
P(x)/Q(x)=0,
где P(x) и Q(x) — многочлены, причем Q(x)≢0. Его корнями являются все нули многочлена P(x),

за исключением тех, которые являются нулями многочлена Q(x). Другими словами, это уравнение эквивалентно системе
{P(x)=0, Q(x)≠0.
Слайд 4Рациональные неравенства и пример
P(x)/Q(x)>0, P(x)/Q(x)<0, P(x)/Q(x)⩾0, P(x)/Q(x)⩽0,
где P(x) и Q(x) — многочлены, причем Q(x)≢0.

Слайд 5Пропорция — это просто равенство двух дробей
a/b=c/d
.





 Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи
Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи Вопросы для повторения по информатике и математике
Вопросы для повторения по информатике и математике График функции
График функции Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Понятие производной
Понятие производной Алгоритм Евклида
Алгоритм Евклида Деятельностный подход при изучении темы Объёмы в 5 и 6 классах
Деятельностный подход при изучении темы Объёмы в 5 и 6 классах Цилиндр
Цилиндр Осевая и центральная симметрия
Осевая и центральная симметрия Площадь криволинейной трапеции
Площадь криволинейной трапеции Правильные многогранники
Правильные многогранники Задачи на проценты
Задачи на проценты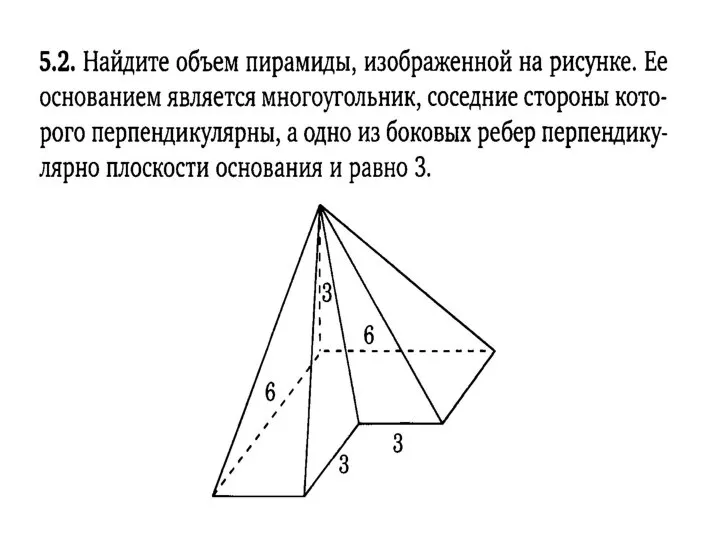 Объемы. Объем параллелепипеда
Объемы. Объем параллелепипеда Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Пространственные и временные представления
Пространственные и временные представления Преобразования графиков функций
Преобразования графиков функций Частота и вероятность случайного события
Частота и вероятность случайного события Эконометрика. Оценка влияния количественных показателей друг на друга
Эконометрика. Оценка влияния количественных показателей друг на друга Действительный анализ. Интеграл Лебега
Действительный анализ. Интеграл Лебега Сумма углов треугольника
Сумма углов треугольника Кто хочет стать миллионером. Математическая игра
Кто хочет стать миллионером. Математическая игра Оптимальное управление динамических систем. Гамильтониан и принцип максимума
Оптимальное управление динамических систем. Гамильтониан и принцип максимума Круг и шар
Круг и шар Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Вычитание натуральных чисел
Вычитание натуральных чисел Решение тригонометрических неравенств
Решение тригонометрических неравенств Vorlesung. Blatt 2
Vorlesung. Blatt 2