Классические алгоритмы на графах

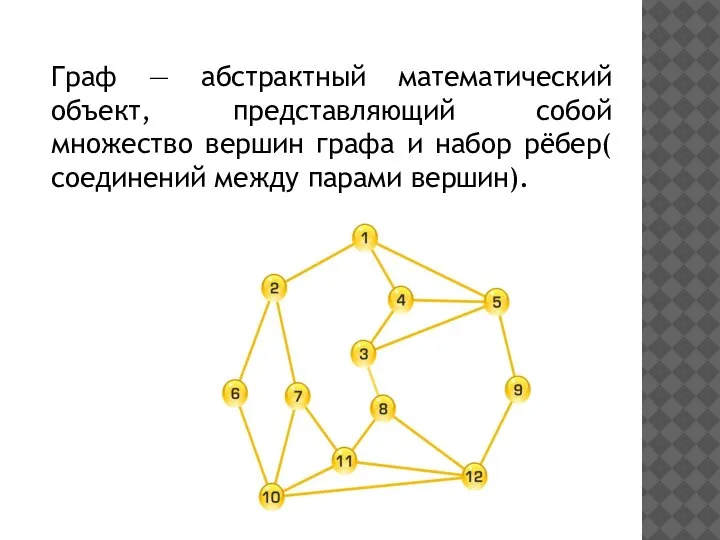
Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер( соединений между парами вершин).

ВИДЫ ГРАФОВ
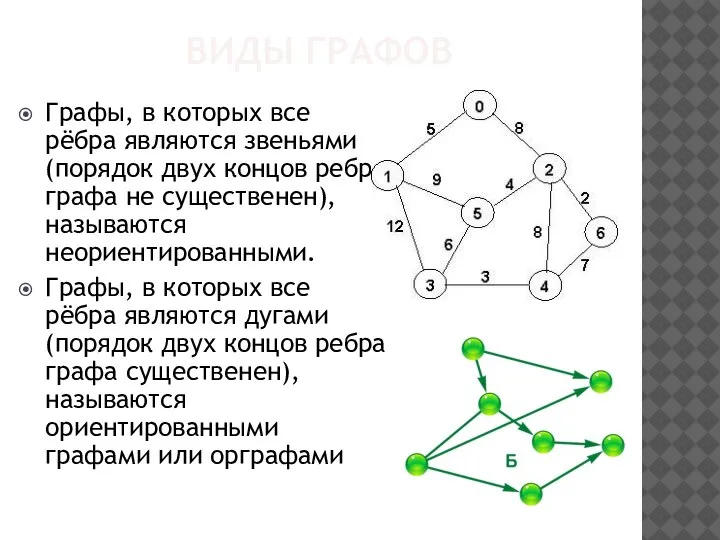
Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.
Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами

АЛГОРИТМ ДЕЙКСТРЫ
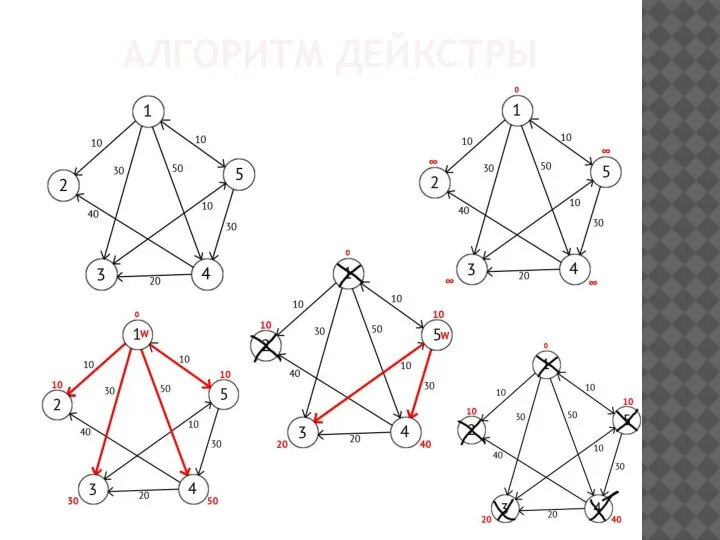
Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных.
Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом.

АЛГОРИТМ ДЕЙКСТРЫ

АЛГОРИТМ КРАСКАЛА
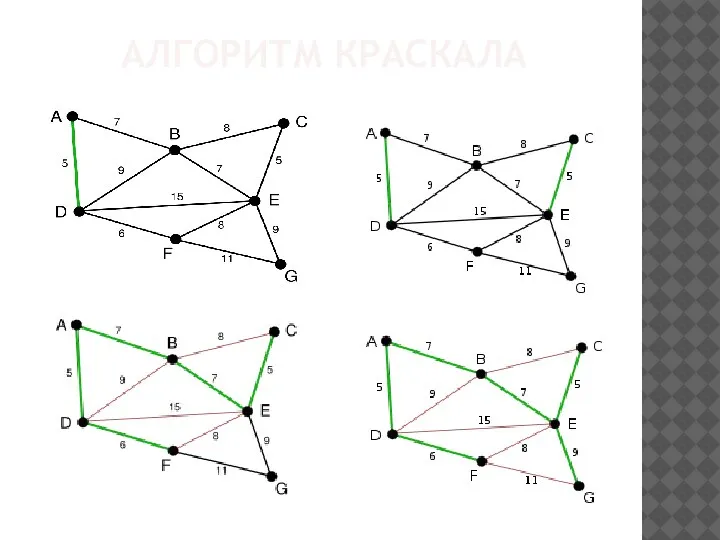
Алгоритм Краскала — эффективный алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Также алгоритм используется для нахождения некоторых приближений для задачи Штейнера. Алгоритм впервые описан Джозефом Крускалом в 1956 году.

АЛГОРИТМ КРАСКАЛА

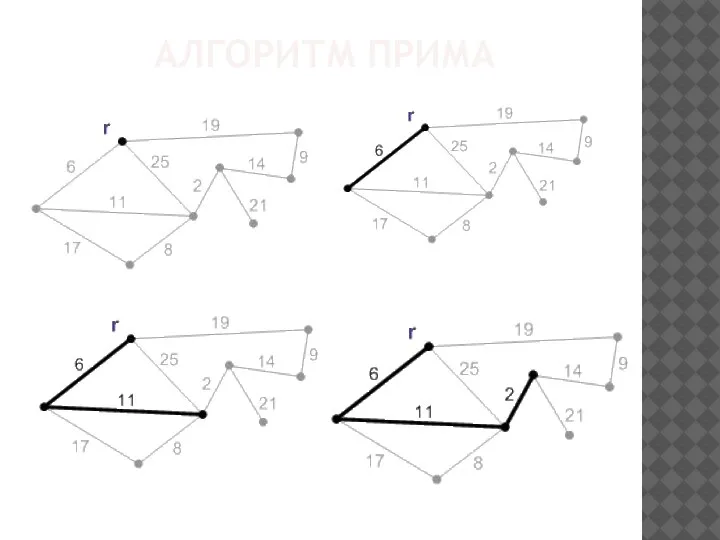
АЛГОРИТМ ПРИМА
Алгоритм Прима — это алгоритм поиска минимального остовного дерева в связном графе. С помощью алгоритма Прима можно выделить только те ребра графа, с помощью которых можно соединить каждую из вершин этого графа и при этом суммарная стоимость этих ребер будет минимальна.

АЛГОРИТМ ПРИМА