Коллинеарные векторы

Если векторы и коллинеарные и их лучи направлены в одну сторону, то векторы называются сонаправленными.
Обозначаются : а↑↑b.
Если векторы коллинеарные, а их лучи направлены в разные стороны, то векторы называются противоположно направленными.
Обозначаются : a↑↓d.
Нулевой вектор считают сонаправленным с любым вектором.

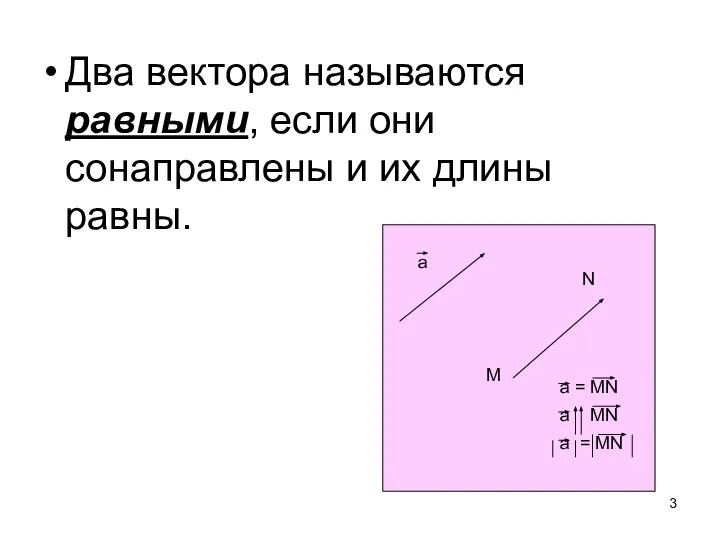
Два вектора называются равными, если они сонаправлены и их длины равны.

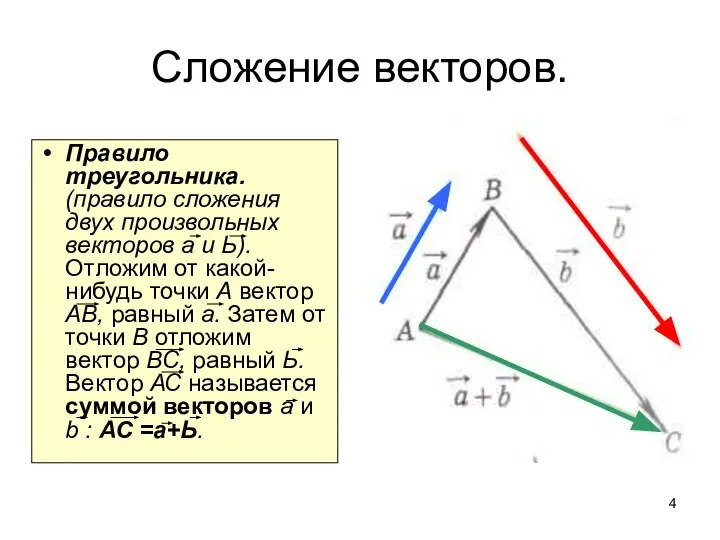
Сложение векторов.
Правило треугольника. (правило сложения двух произвольных векторов а и Ь). Отложим от какой-нибудь точки А вектор АВ, равный а. Затем от точки В отложим вектор ВС, равный Ь. Вектор АС называется суммой векторов а и b : АС =а+Ь.

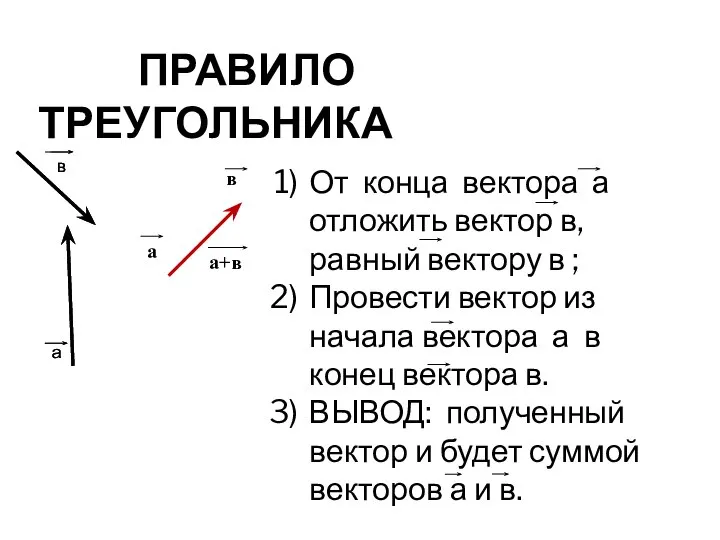
От конца вектора а отложить вектор в, равный вектору в ;
Провести вектор из начала вектора а в конец вектора в.
ВЫВОД: полученный вектор и будет суммой векторов а и в.
ПРАВИЛО ТРЕУГОЛЬНИКА
а+в
в
а
а
в
в
а

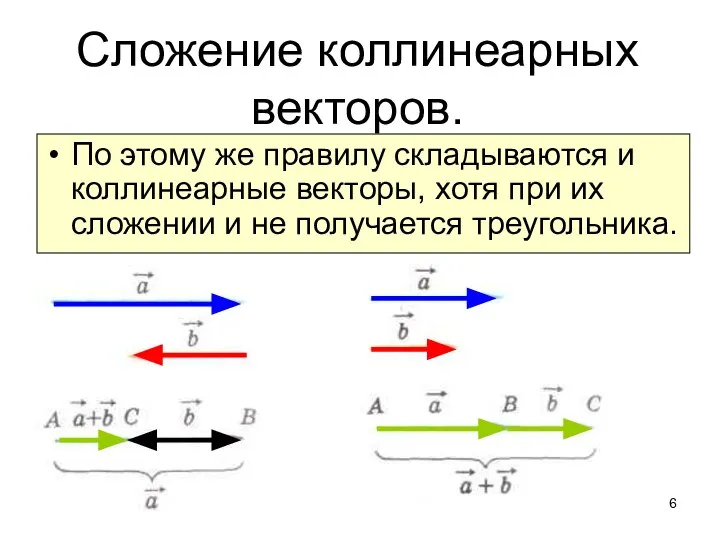
Сложение коллинеарных векторов.
По этому же правилу складываются и коллинеарные векторы, хотя при их сложении и не получается треугольника.

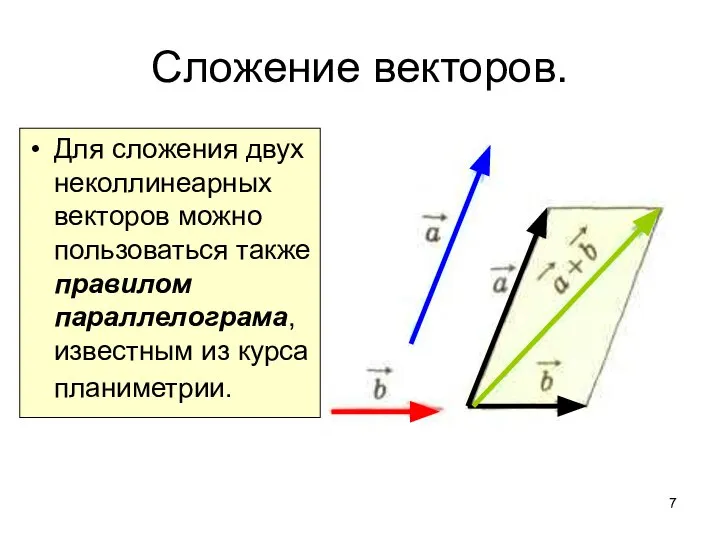
Сложение векторов.
Для сложения двух неколлинеарных векторов можно пользоваться также правилом параллелограма, известным из курса планиметрии.

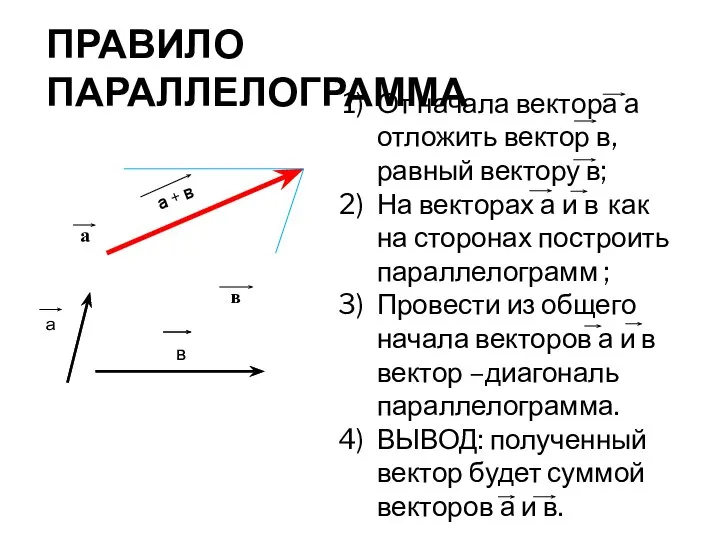
а + в
ПРАВИЛО ПАРАЛЛЕЛОГРАММА
От начала вектора а отложить вектор в, равный вектору в;
На векторах а и в как на сторонах построить параллелограмм ;
Провести из общего начала векторов а и в вектор –диагональ параллелограмма.
ВЫВОД: полученный вектор будет суммой векторов а и в.
а
в
а
в

Свойства сложения векторов.
Для любых векторов а, b и с справедливы равенства:
а + b = b + a
(переместительный закон);
(a + b) + c = a + (b + с)
(сочетательный закон).

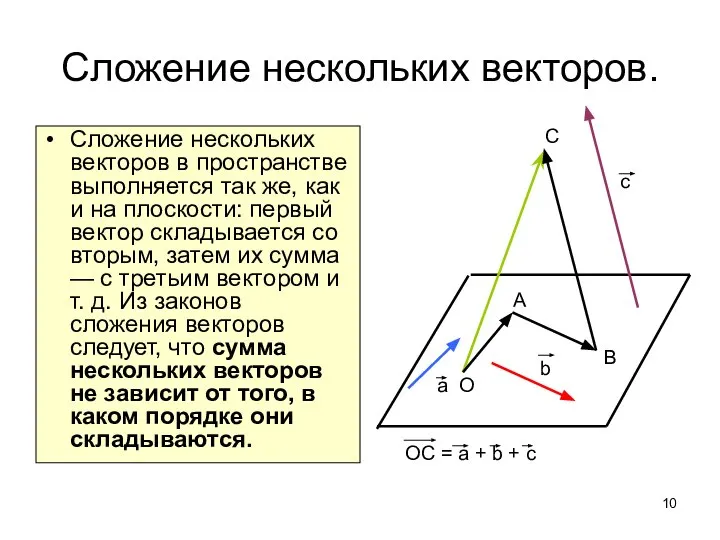
Сложение нескольких векторов.
Сложение нескольких векторов в пространстве выполняется так же, как и на плоскости: первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.

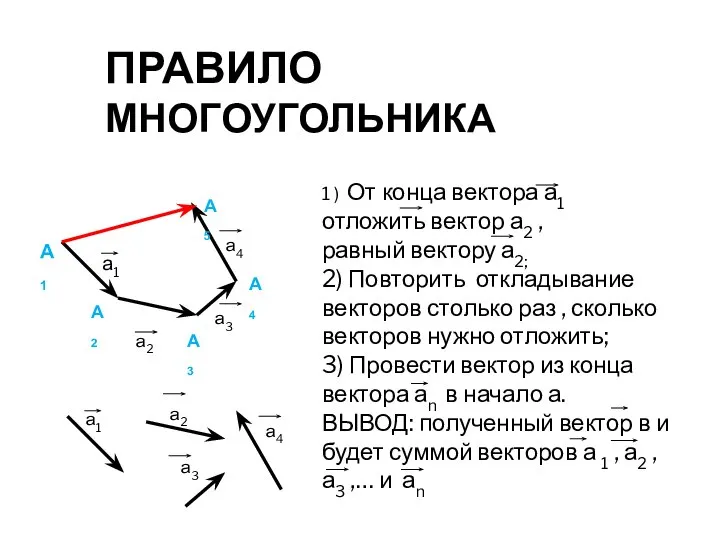
ПРАВИЛО МНОГОУГОЛЬНИКА
а1
а2
а3
а4
А1
А2
А3
А4
А5
1 ) От конца вектора а1 отложить вектор а2 ,
равный вектору а2;
2) Повторить откладывание векторов столько раз , сколько векторов нужно отложить;
3) Провести вектор из конца вектора аn в начало а.
ВЫВОД: полученный вектор в и будет суммой векторов а 1 , а2 , а3 ,… и аn
а1
а2
а3
а4

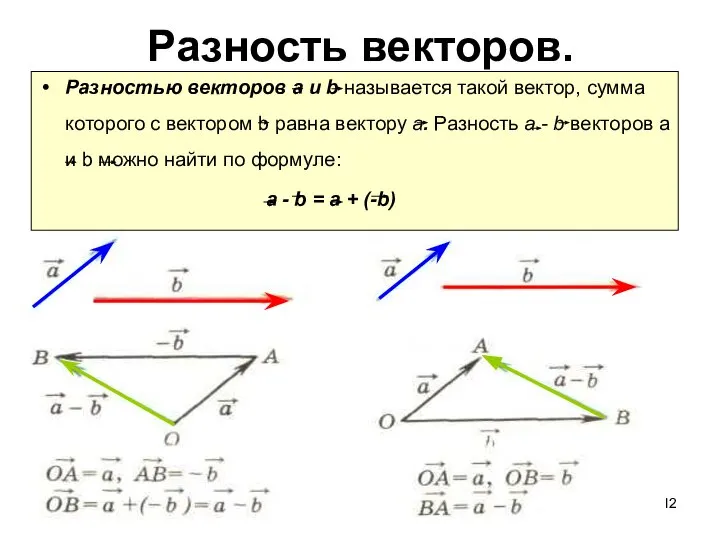
Разность векторов.
Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а. Разность а - b векторов а и b можно найти по формуле:
а - b = а + (-b)

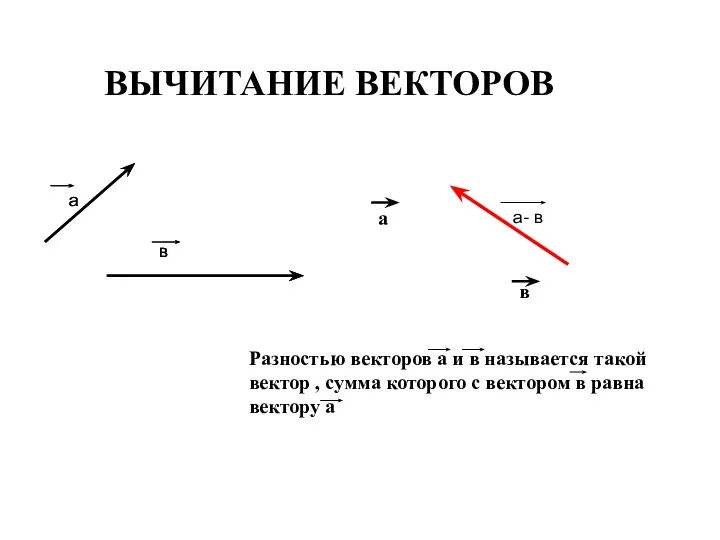
ВЫЧИТАНИЕ ВЕКТОРОВ
а
в
а- в
Разностью векторов а и в называется такой вектор , сумма которого с вектором в равна вектору а
а
в
а
в

Умножение вектора на число.
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого
равна |k|*|а|, причем векторы а и b сонаправлены при k O и противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение вектора а на число k обозначается так: ka.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведение любого вектора на число нуль есть нулевой вектор.

Правила умножения вектора на число.
Для любых векторов а, b и любых чисел k, f справедливы равенства:
(kf)a=k(fa) ( сочетательный закон);
k(a + b)= ka + kb (первый распределительный закон);
(k + f) a =ka + fa (второй распределительный закон).

Свойства умножения вектора на число.
Отметим, что (-1)а является вектором, противоположным вектору а, т.е.
(-1)a = -а.
если вектор а ненулевой, то векторы (-1)а и а противоположно направлены.
если векторы а и b коллинеарны и а О, то существует число k такое, что b= ka.

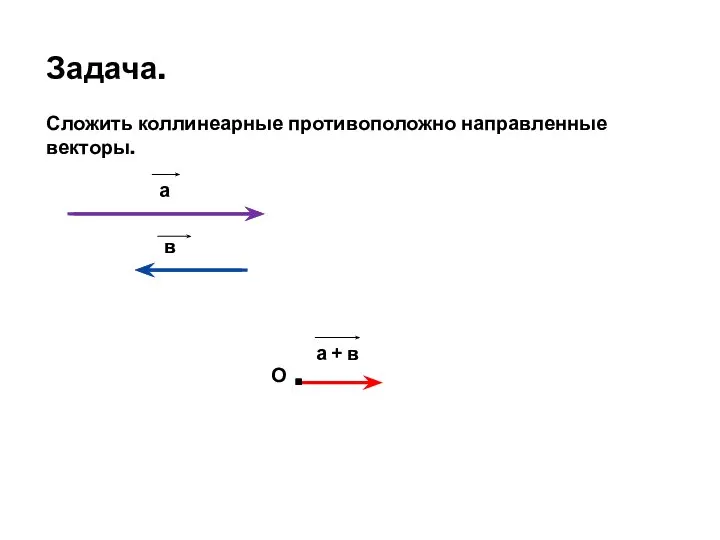
Задача.
Сложить коллинеарные противоположно направленные векторы.
а
в
О
а + в
.

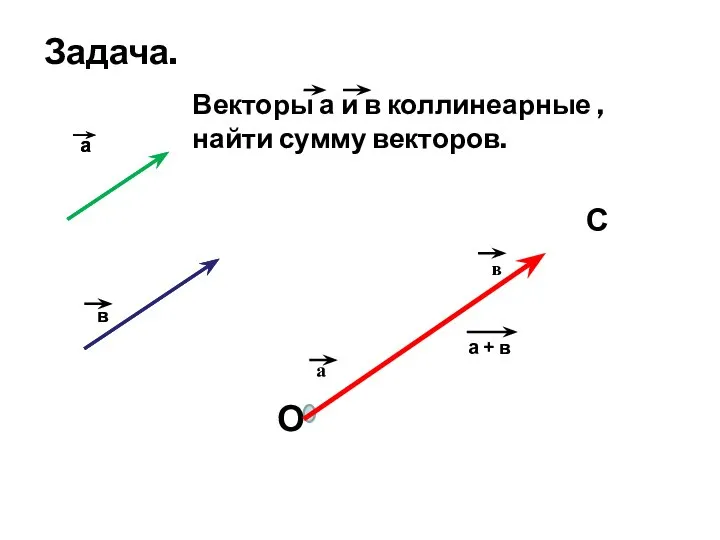
а
в
Векторы а и в коллинеарные , найти сумму векторов.
О
С
а + в
а
а
в
Задача.

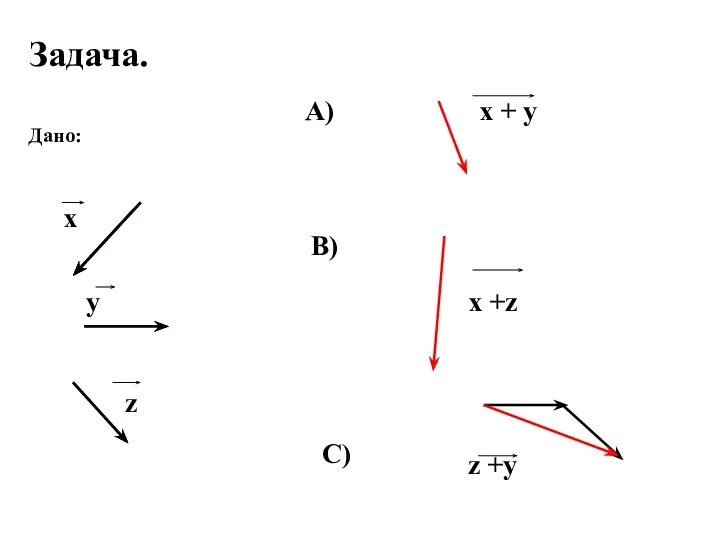
Задача.
Дано:
х
у
z
А)
х + y
В)
x +z
C)
z +y

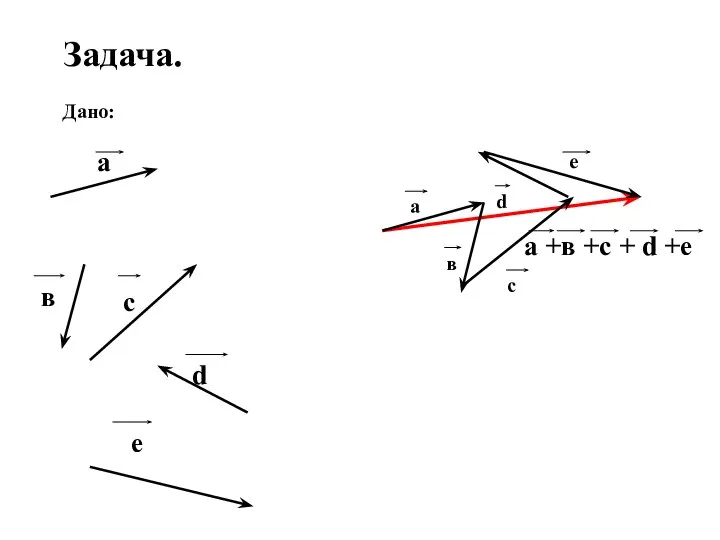
Задача.
Дано:
а
в
с
d
е
а +в +с + d +е
а
в
с
d
e

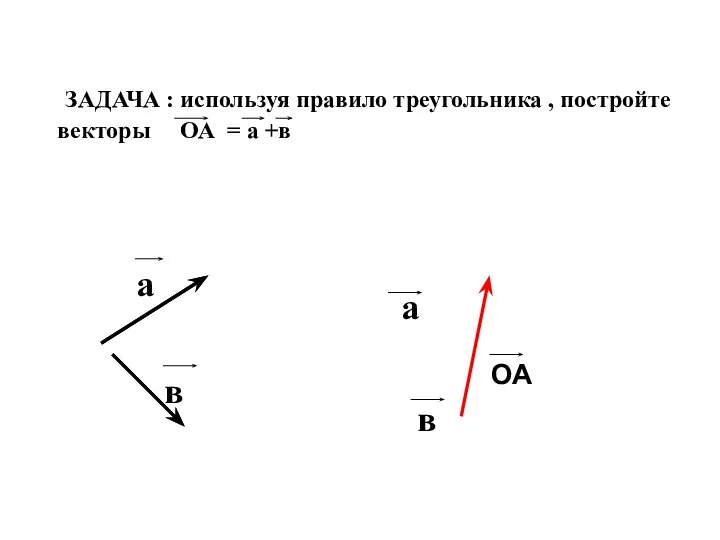
ЗАДАЧА : используя правило треугольника , постройте векторы ОА = а +в
а
в
в
ОА
а

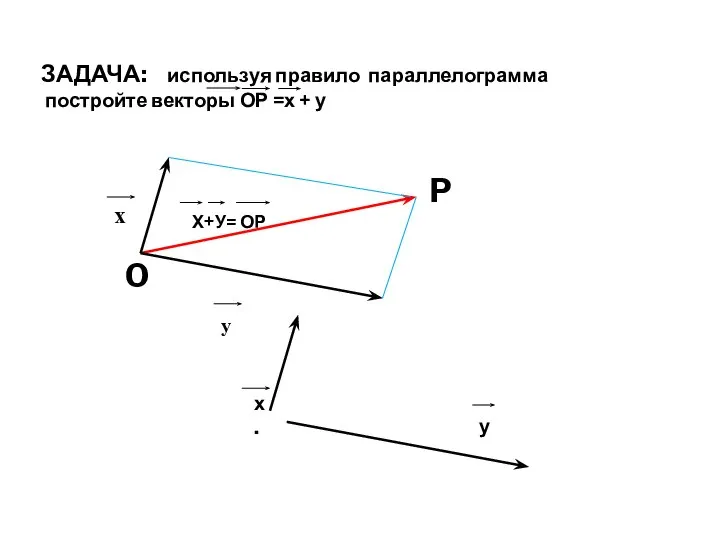
ЗАДАЧА: используя правило параллелограмма
постройте векторы ОР =х + у
Х+У= ОР
O
P
х.
у
х
у