Содержание
- 2. Почему линейные модели до сих пор используются? Очень простые, поэтому можно использовать там, где нужна интерпретируемость
- 3. Постановка задачи Датасет: Функция потерь:
- 4. Определение модели Мы будем искать модель в следующем виде Намного удобнее для записи внести 1 в
- 5. Линейность по параметрам Какое может быть происхождение у признаков ? Просто численный признак Преобразования численных признаков
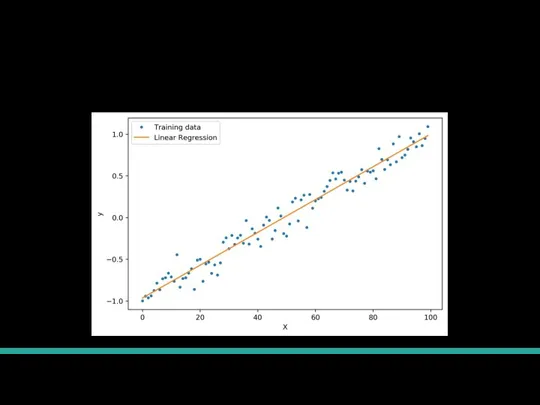
- 6. Пример
- 7. Точное решение Запишем то, что мы хотим получить:
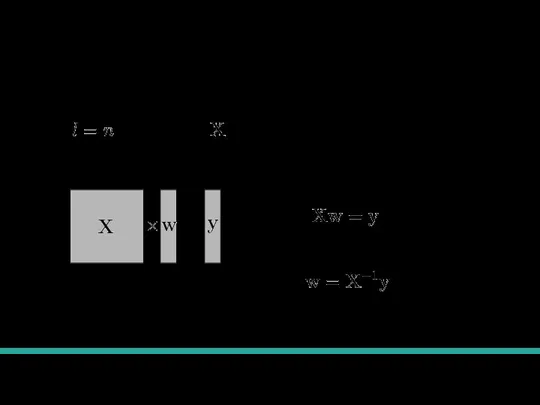
- 8. Точное решение Случай , тогда матрица - квадратная и может иметь обратную. = Система линейных уравнений:
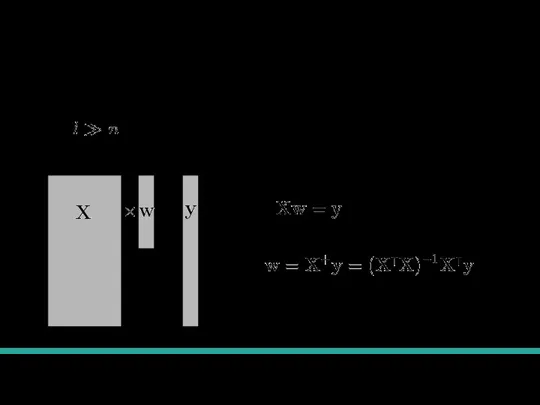
- 9. Pseudo-Inverse Обычно , тогда у нас переопределенная система линейных уравнений. = Система линейных уравнений: Приближенное решение:
- 10. Получение решения через производную Подставим выражение для в функцию потерь и запишем в векторном виде: Возьмем
- 11. Обучение классификаторов
- 12. Получение решения через производную Возьмем производную Если у линейно независимые столбцы, то можно приравнять производную к
- 13. Постановка задачи Датасет: Функция потерь: , . То есть это вектор из 0 и 1 Будет
- 14. Мы хотим выбрать функцию потерь, но какая лучше всего подойдет не знаем. Попробуем искать лучшую модель
- 15. Вероятностная модель Х- случайная величина вектор признаков. Y- случайная величина целевая переменная. Пример случайной модели (клики
- 16. Функция правдоподобия Найдем способ для обучения любой модели, предсказывающей вероятность принадлежности к классу. - вектор признаков,
- 17. Обучение модели через максимальное правдоподобие Теорема из статистики гарантирует, что если мы найдем параметры модели, которые
- 18. Связь с минимизацией функции потерь Преобразуем задачу максимизации в задачу минимизации. Мы видим что минимизация полученного
- 19. Что мы сделали Мы знаем, что максимизация правдоподобия дает хорошие веса из статистики. Изменив формулу, мы
- 20. Логистическая регрессия
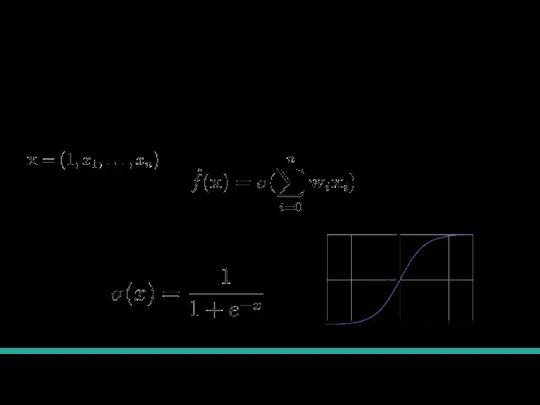
- 21. Определение модели Мы будем искать модель в следующем виде. Определение сигмоиды:
- 22. Предсказание вероятности Будем считать, что наша модель предсказывает вероятности. Именно поэтому она называется регрессией. Вероятносвть для
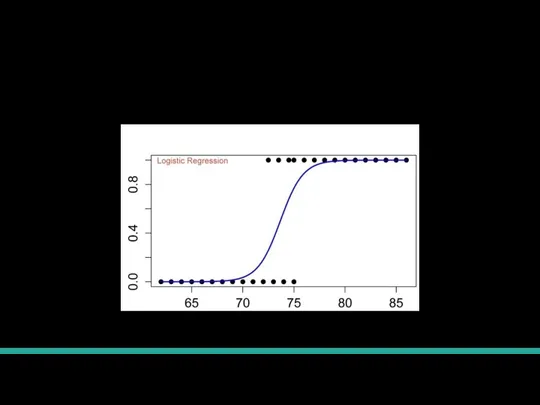
- 23. Пример работы Как выглядит обученная логистическая регрессия на данных с одним признаком.
- 24. Обучение логистической регрессии В полученную ранее формулу функции потерь можно подставить вероятность, которую предсказывает логистическая регрессия.
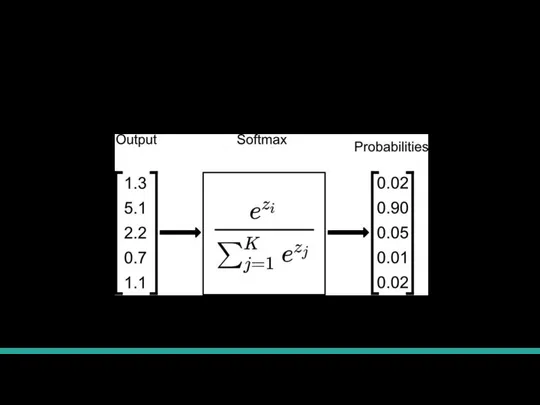
- 25. Обобщение на много классов Пусть у нас есть m классов. Введем две новые функции:
- 26. Пример работы Softmax
- 27. Много классов Выпишем предсказанную вероятность для к-го класса. Ее можно подставить в функцию потерь для произвольного
- 28. Градиентный спуск
- 29. Обучение логистической регрессии В полученную ранее формулу функции потерь можно подставить вероятность, которую предсказывает логистическая регрессия.
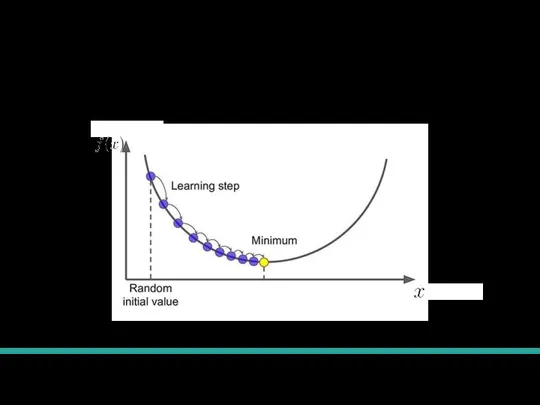
- 30. Эвристика градиентного спуска
- 31. Градиентный спуск формализация У нас стоит задача минимизации какой-то функции: Чтобы применять метод градиентного спуска нужно
- 32. Шаг градиентного спуска На каждом шаге будем менять все переменные, от которых зависит функция: ... Или
- 33. Градиентный спуск Выбираем точку, с которой начнем оптимизацию. На каждом шаге будем менять все переменные, от
- 34. Градиентный спуск для параболы Будем минимизировать , / / Теперь делаем обновления: С каждым шагом мы
- 35. Градиентный спуск для линейной регрессии Функция потерь (она зависит только от весов, потому что изменять мы
- 36. Градиентный спуск для линейной регрессии Пошагово возьмем производную лосса по параметрам:
- 37. Градиентный спуск для линейной регрессии Функция потерь (она зависит только от весов, потому что изменять мы
- 38. Градиентный спуск для линейной регрессии Будем минимизировать Как-то выберем начальные веса. Теперь делаем обновления:
- 39. Градиентный спуск для логистической регрессии Функция потерь:
- 40. Градиентный спуск для логистической регрессии Возьмем производную: Соединим:
- 41. Регуляризация
- 42. Мультиколлинеарность для линейной регрессии Вспомним определение линейной регрессии: Если столбцы матрицы линейно зависимы, то существуют такие
- 43. Weight Decay Мы можем предположить, что веса не должны быть большими по модулю. Изменим функцию потерь,
- 44. Как изменится градиент -регуляризация -регуляризация
- 45. Нормализация признаков
- 46. Что такое нормализация? Мы изменяем признаки в датасете по правилу: - среднее значение j-го признака в
- 47. Зачем? Градиентный спуск и другие методы плохо работают на признаках с очень большим или маленьким масштабом.
- 49. Скачать презентацию













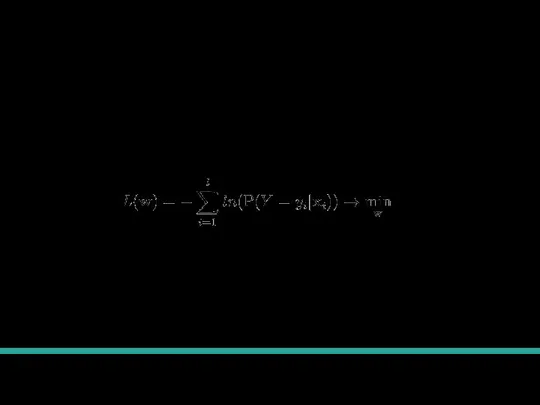
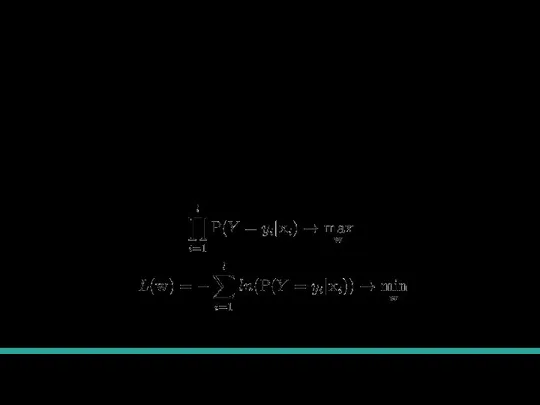










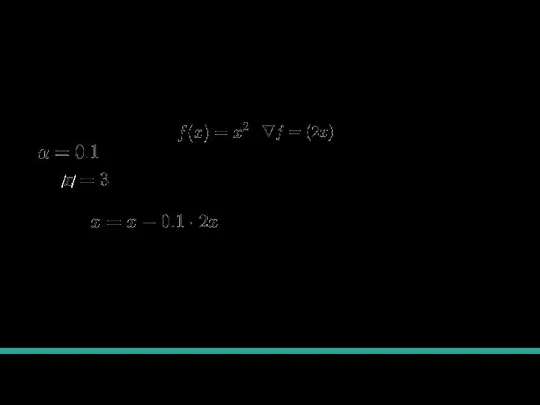
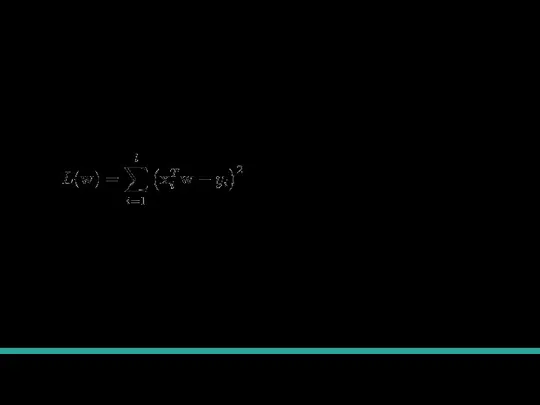












 Средняя линия треугольника
Средняя линия треугольника Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними
Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними Вычисление площадей плоских фигур. Трапеция
Вычисление площадей плоских фигур. Трапеция Комплексные числа
Комплексные числа Объемы многогранников и тел вращения. Практическая работа
Объемы многогранников и тел вращения. Практическая работа Координаты вектора
Координаты вектора Модели и развёртки многогранников
Модели и развёртки многогранников Теорема Пифагора. Исторический экскурс
Теорема Пифагора. Исторический экскурс Волшебный мир геометрических фигур
Волшебный мир геометрических фигур Математика в нашей жизни
Математика в нашей жизни Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ
Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ Дифференциальное исчисление элементарной и сложной функции функции
Дифференциальное исчисление элементарной и сложной функции функции Вычисление логарифмов
Вычисление логарифмов Математический биатлон
Математический биатлон Истинностные задачи
Истинностные задачи Абсолютные, относительные и средние величины. Тема 2
Абсолютные, относительные и средние величины. Тема 2 Произведение многочленов
Произведение многочленов Проценты. Примеры цепочкой
Проценты. Примеры цепочкой Функции и их графики
Функции и их графики Решение примеров
Решение примеров Прямая линия, кривая линия, отрезок, луч
Прямая линия, кривая линия, отрезок, луч Топологические опыты. Мини-урок
Топологические опыты. Мини-урок Презентация на тему Квадрат и куб числа (5 класс)
Презентация на тему Квадрат и куб числа (5 класс)  Треугольники
Треугольники Карта - схема. Бухта знаний
Карта - схема. Бухта знаний Интегралы. Введение в математический анализ
Интегралы. Введение в математический анализ Викторина по эконометрике
Викторина по эконометрике