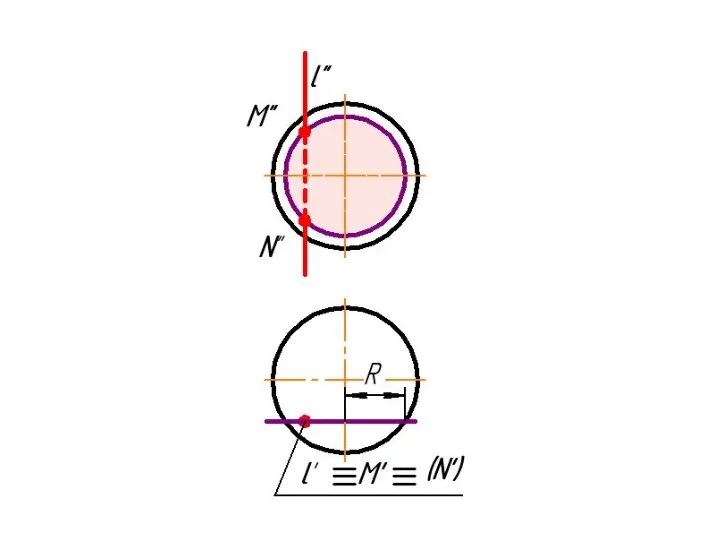
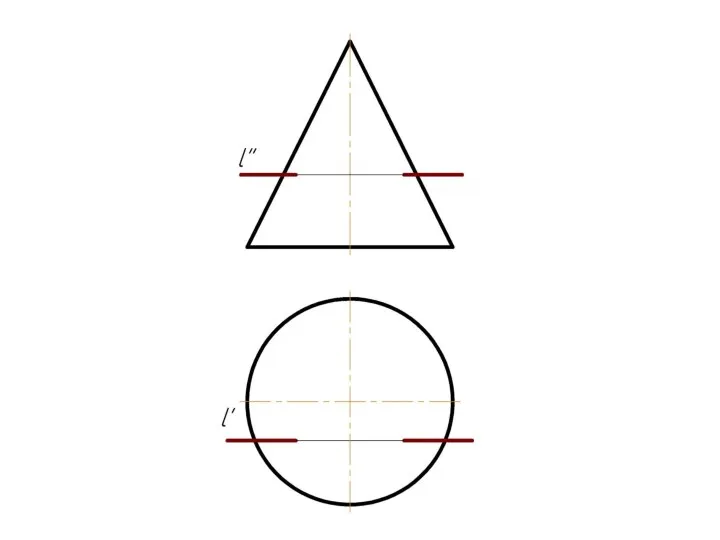
Слайд 2 Плоскость, перпендикулярная к плоскости проекций, проецируется на последнюю в виде прямой

линии.
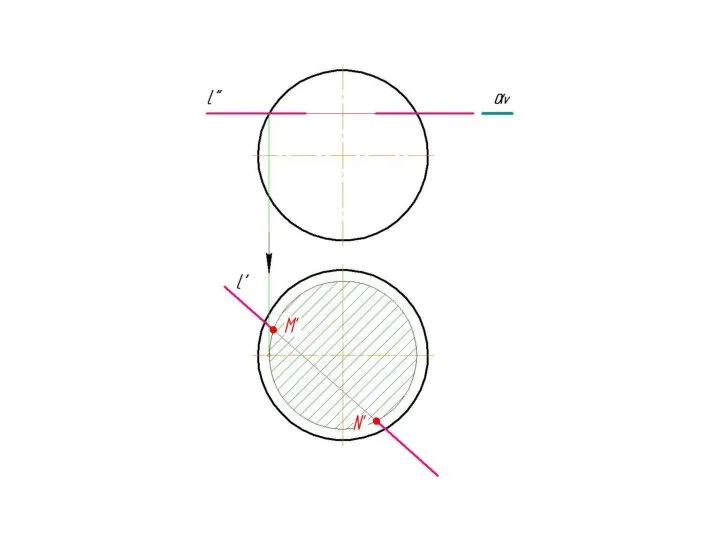
На этой прямой (проекции плоскости) должна находиться соответствующая проекция точки, в которой некоторая прямая пересекает такую плоскость.
Точку пересечения прямой с плоскостью называют также точкой встречи прямой с плоскостью.
Позиционные задачи
Позиционные задачи – это задачи на взаимное расположение геометрических фигур.
1 главная позиционная задача (1 Г.П.З.) – это задача на пересечение линии и поверхности (в частном случае линии и плоскости).
2 главная позиционная задача (2 Г.П.З.) - это задача на пересечение поверхностей (в частном случае плоскостей).
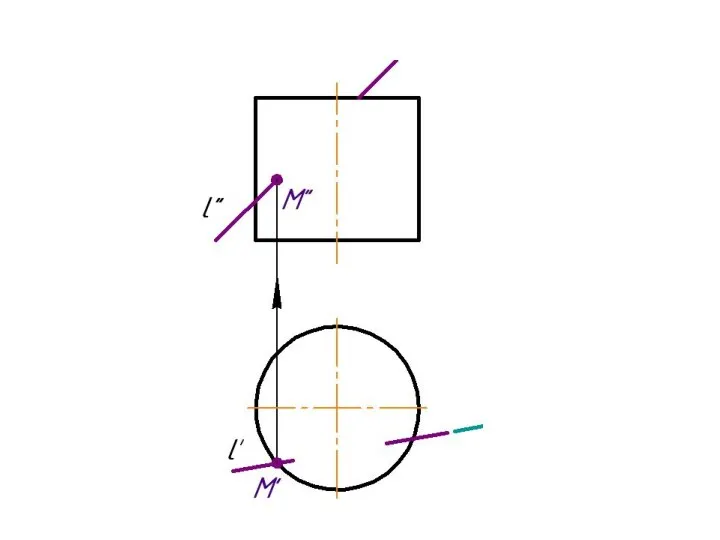
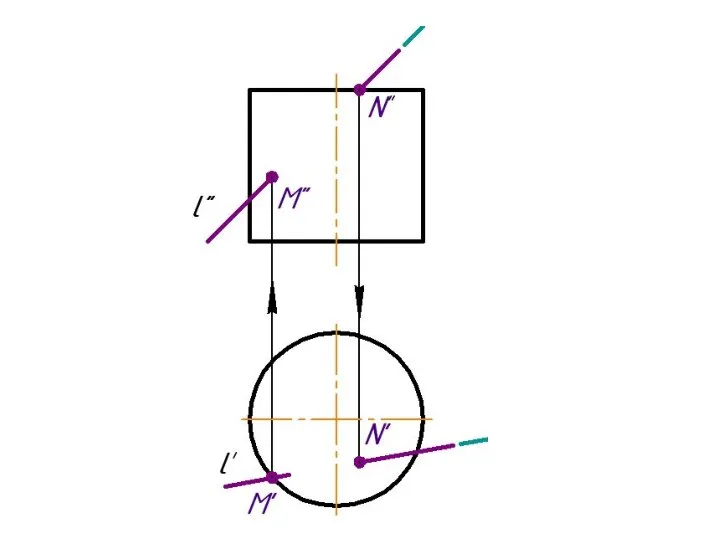
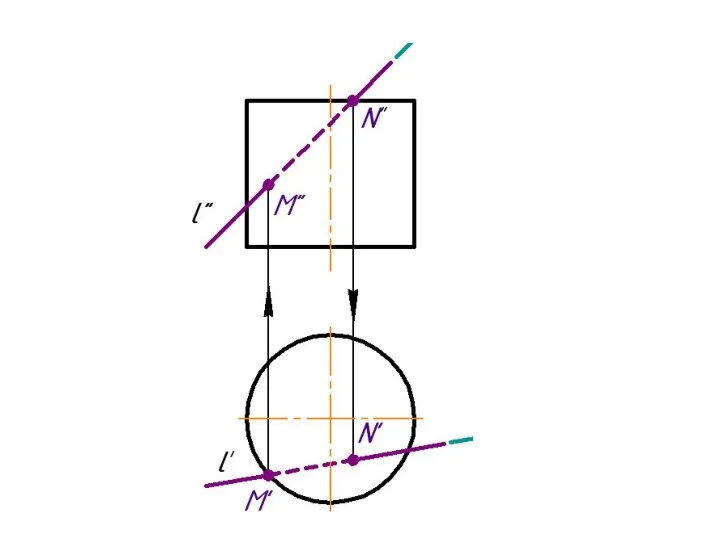
Слайд 3Пересечение прямой с плоскостью в общем случае. Определение видимости.
Дано:
α, l
Найти:
К =
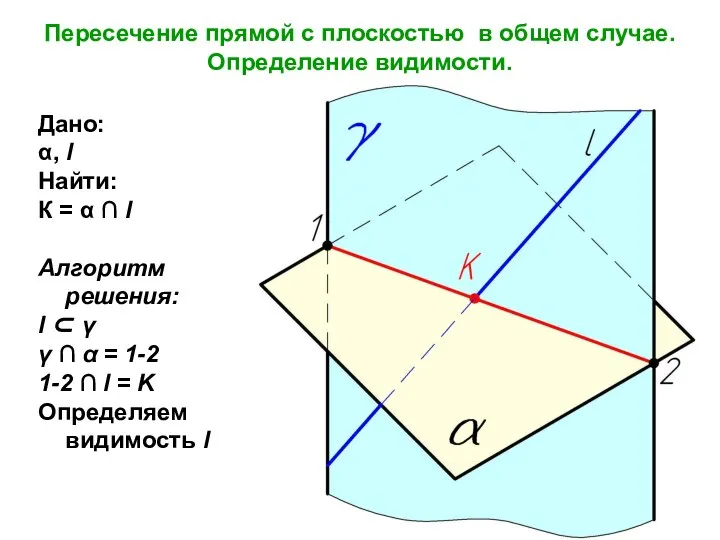
α ∩ l
Алгоритм решения:
l ⊂ γ
γ ∩ α = 1-2
1-2 ∩ l = K
Определяем видимость l
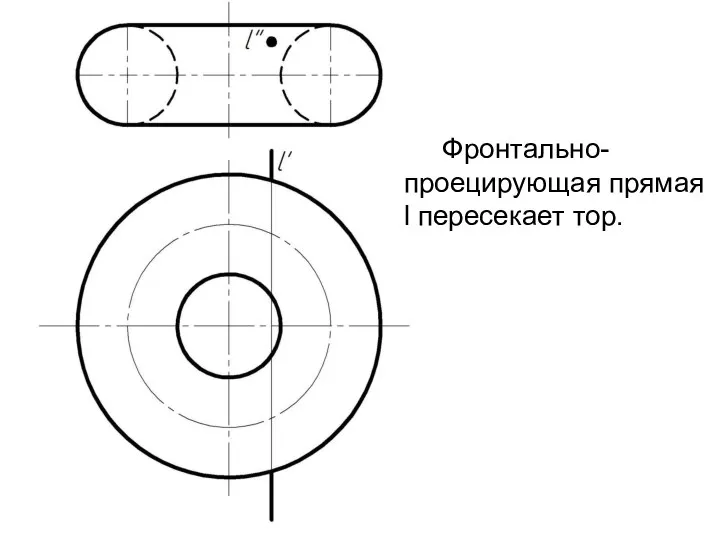
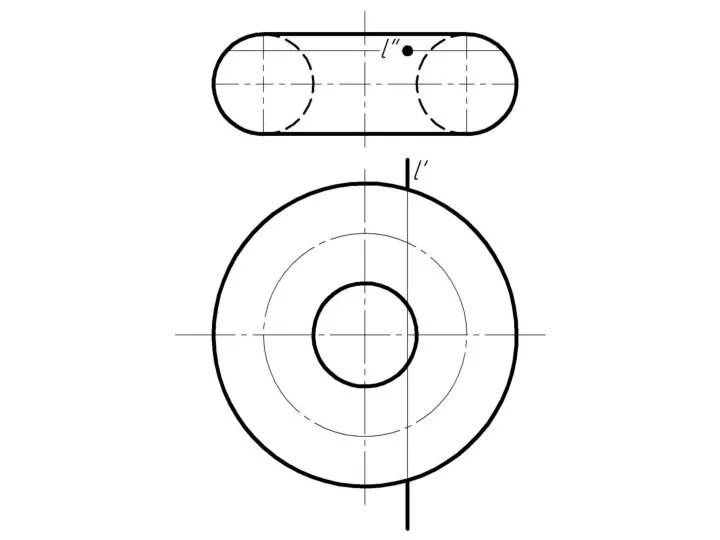
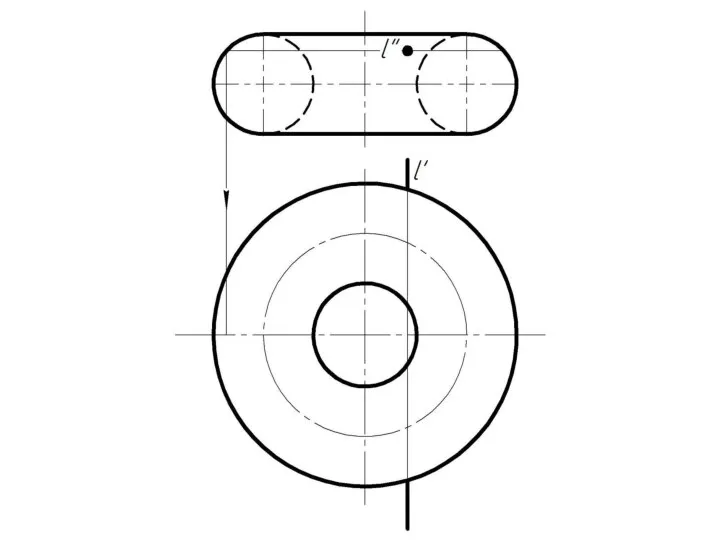
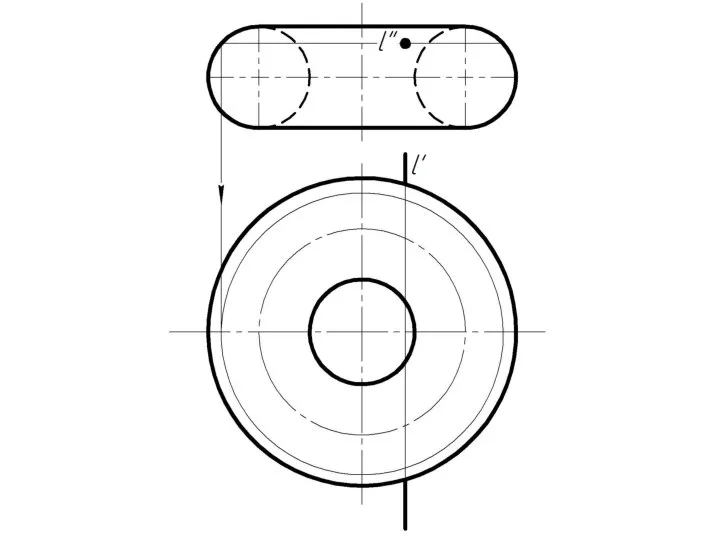
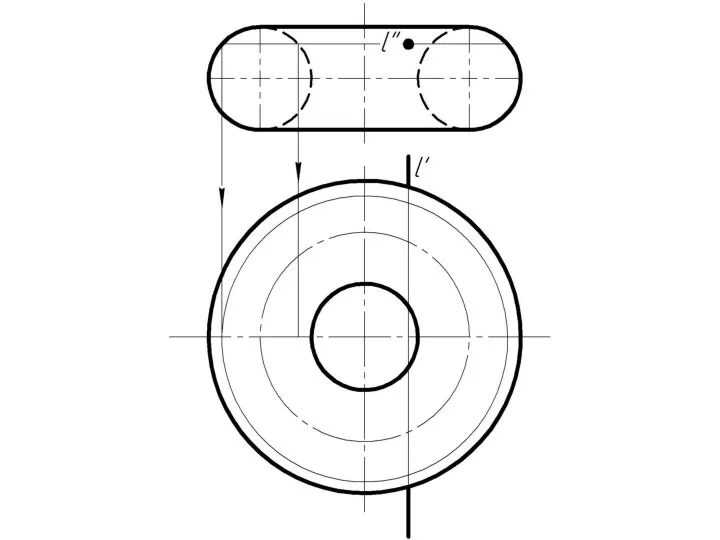
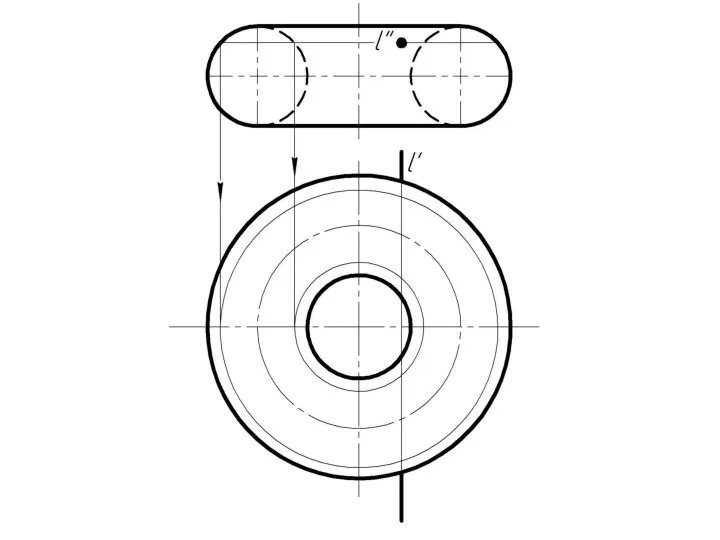
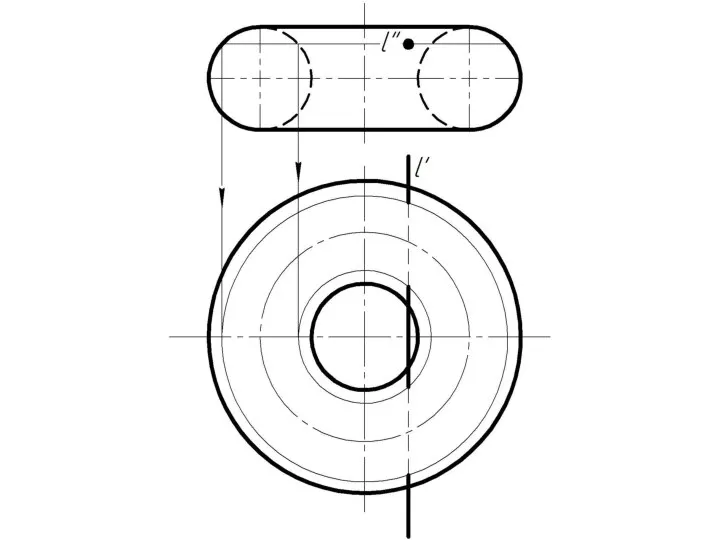
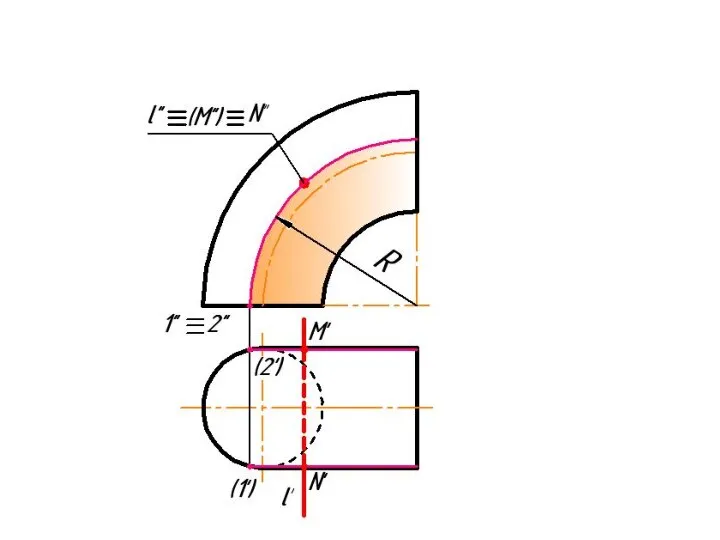
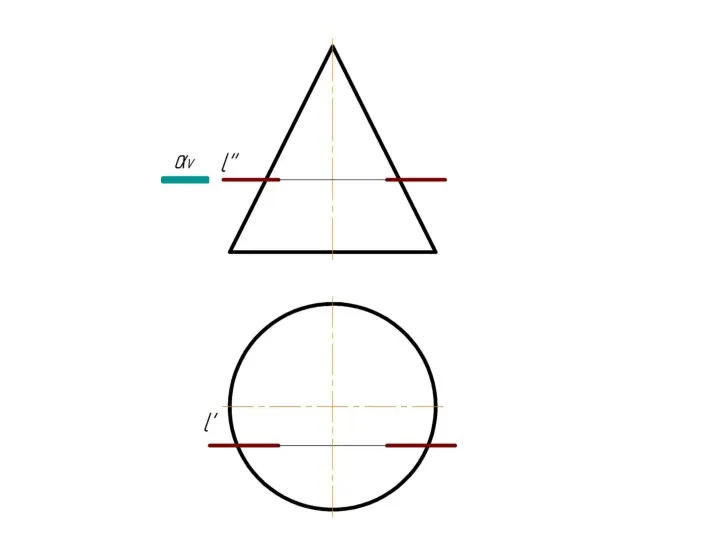
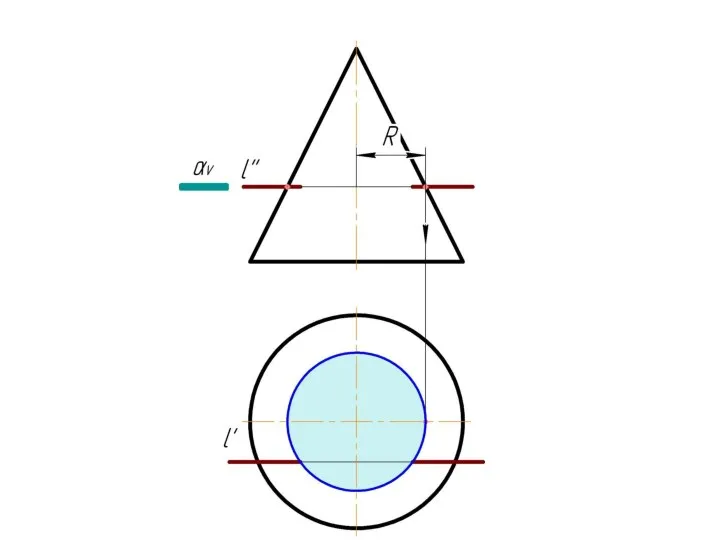
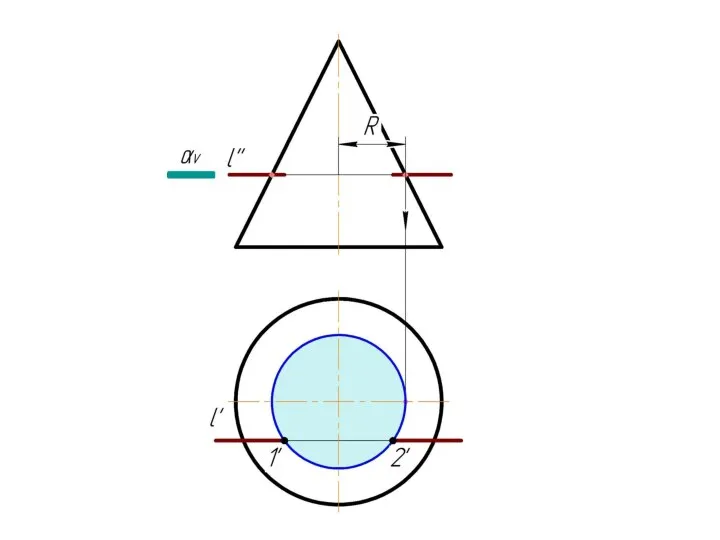
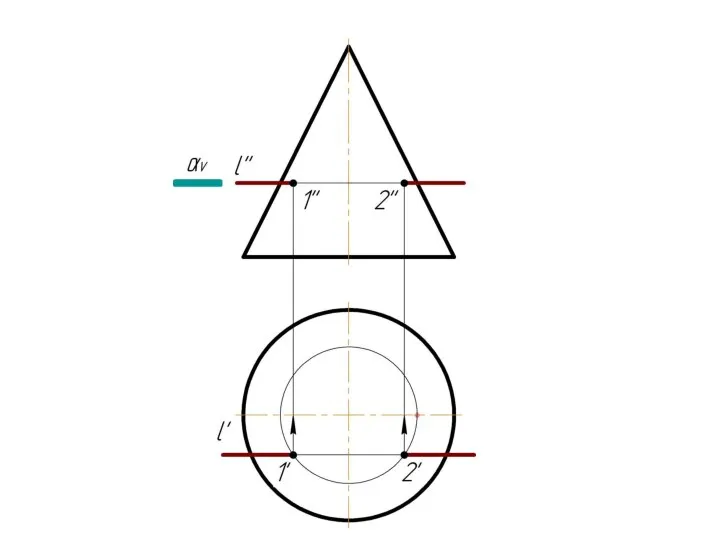
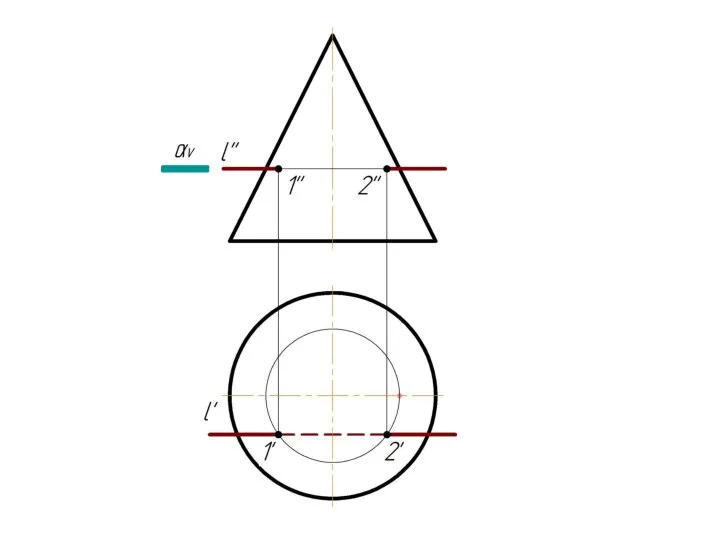
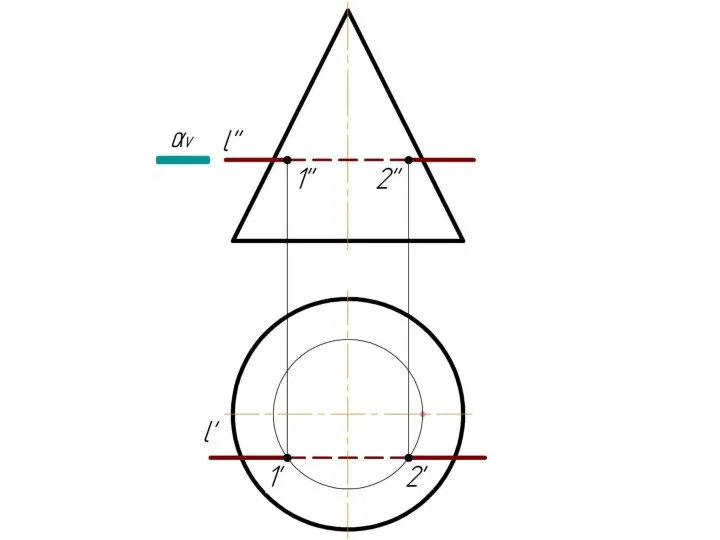
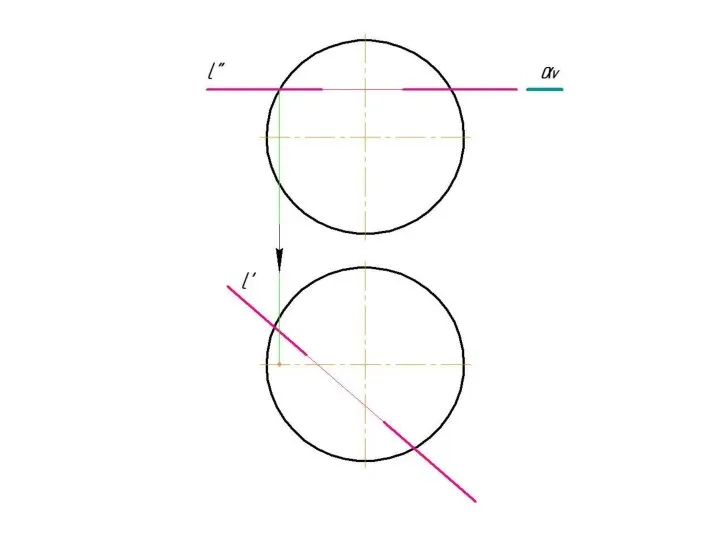
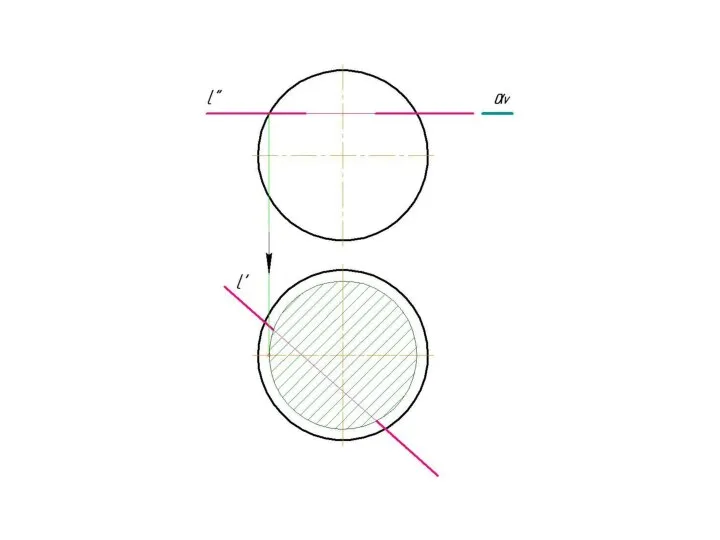
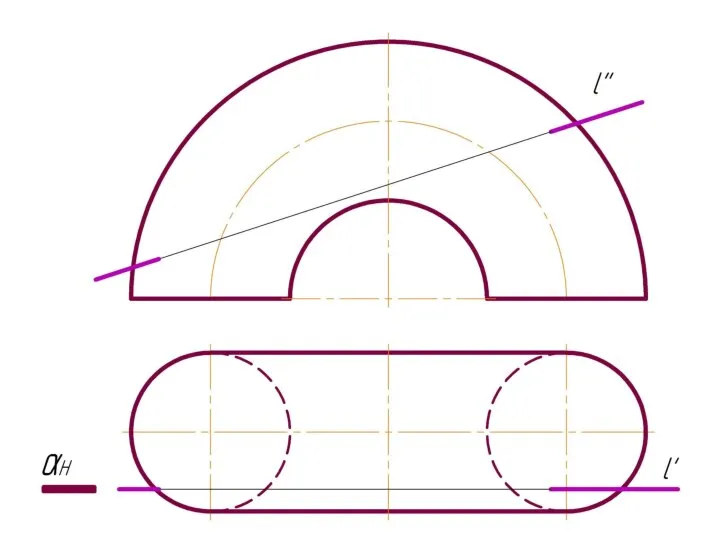
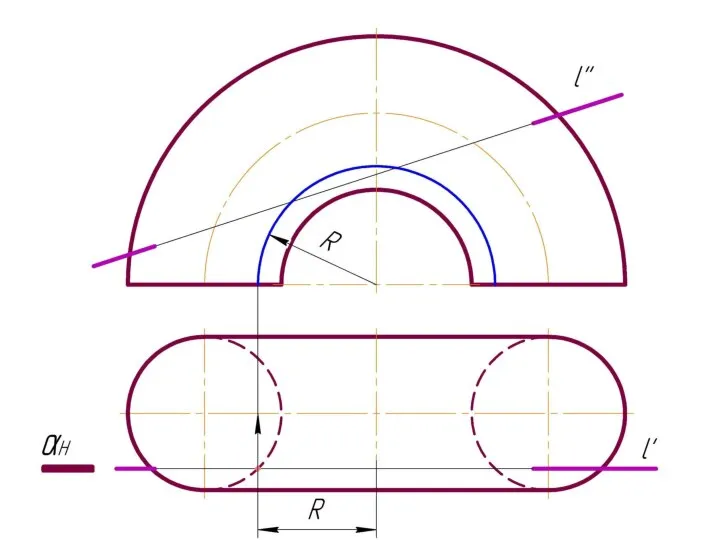
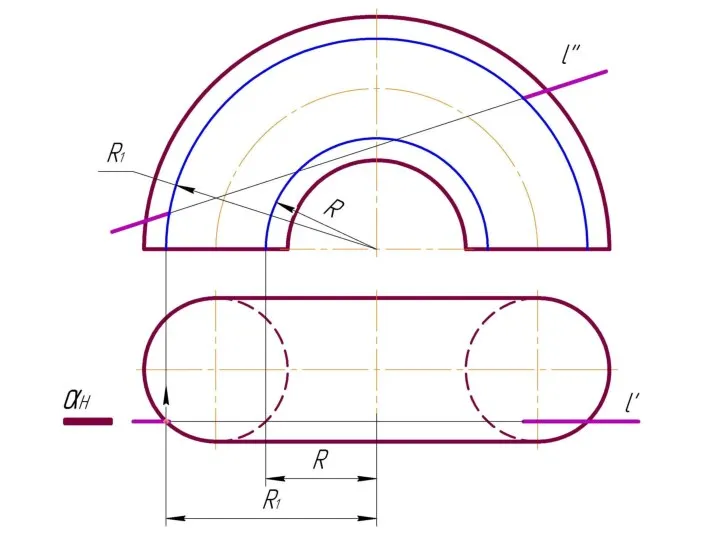
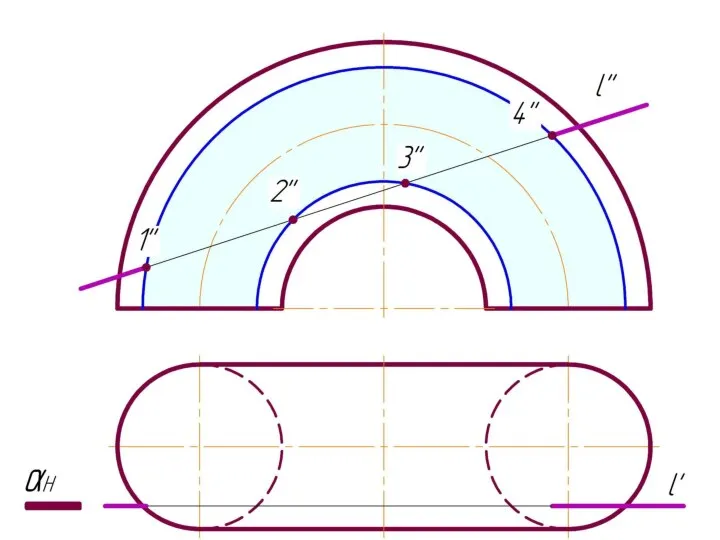
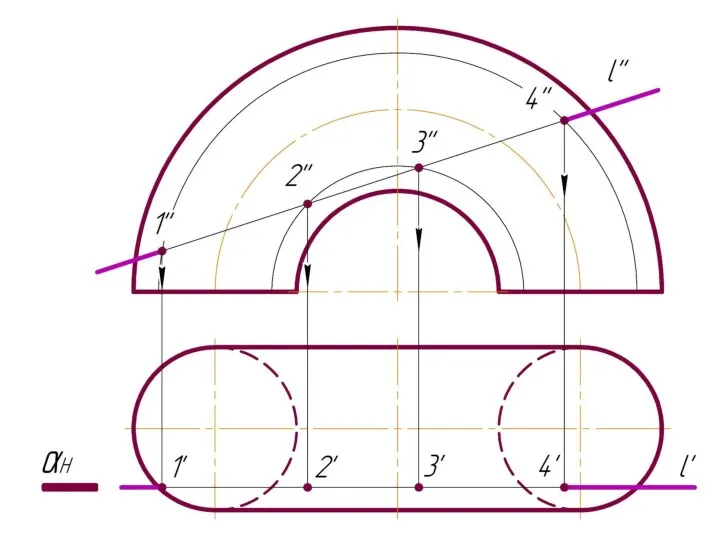
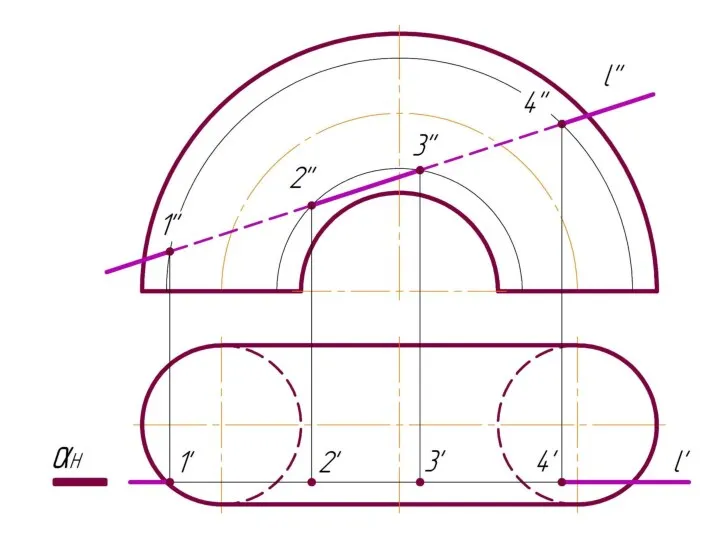
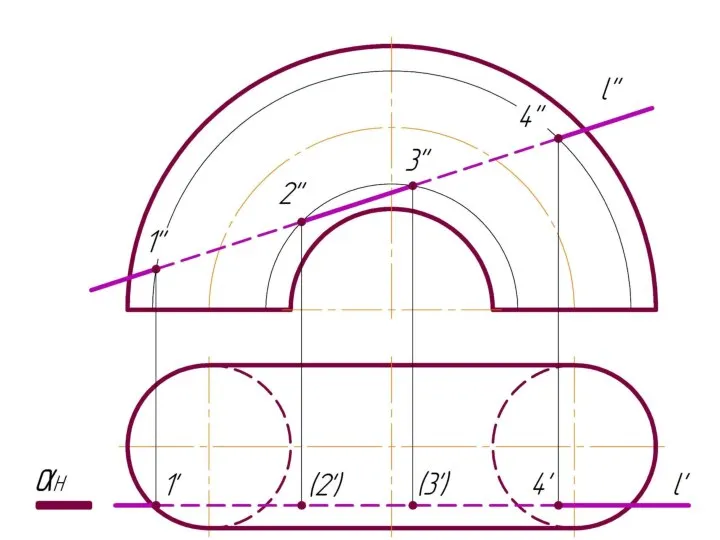
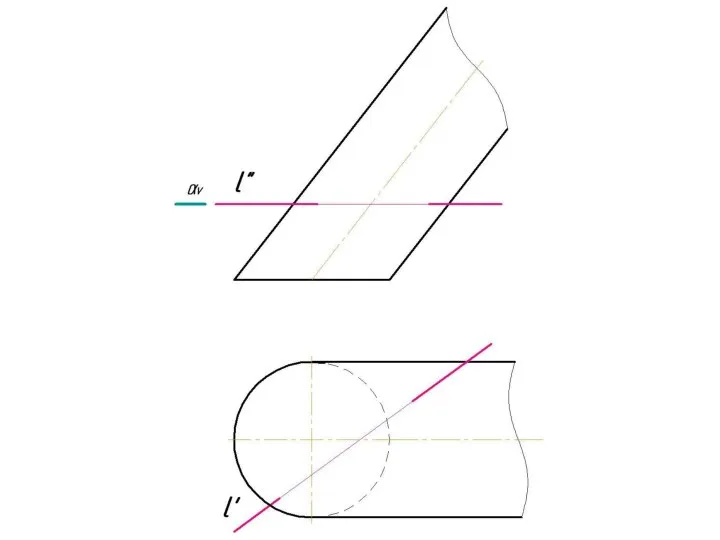
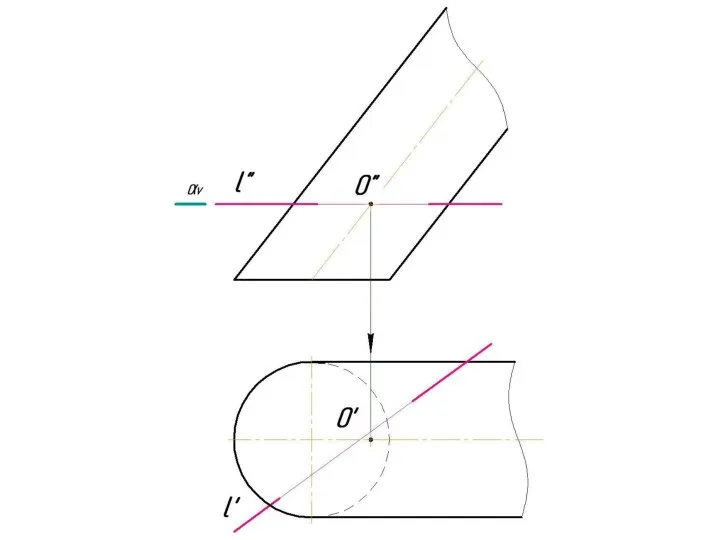
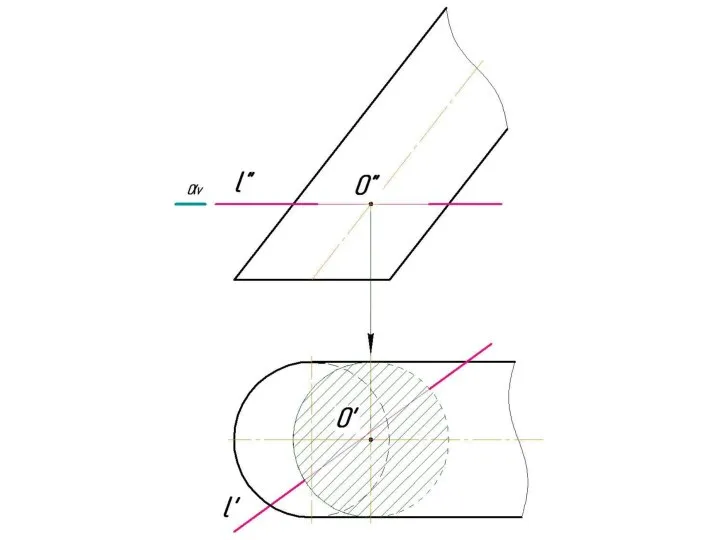
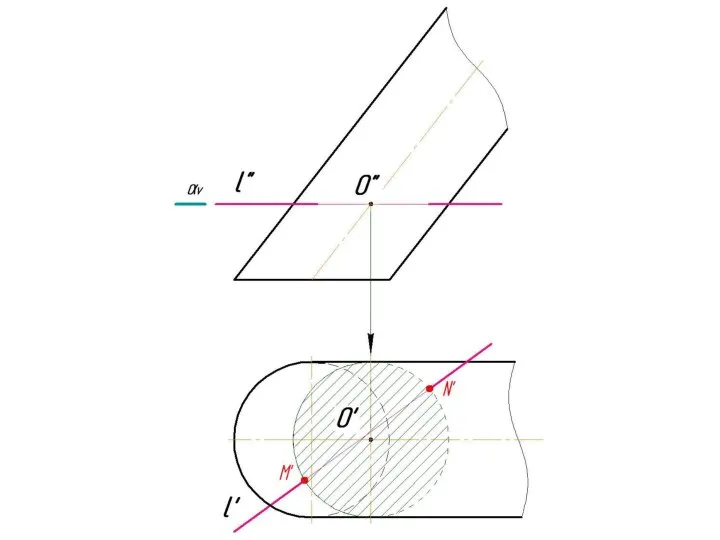
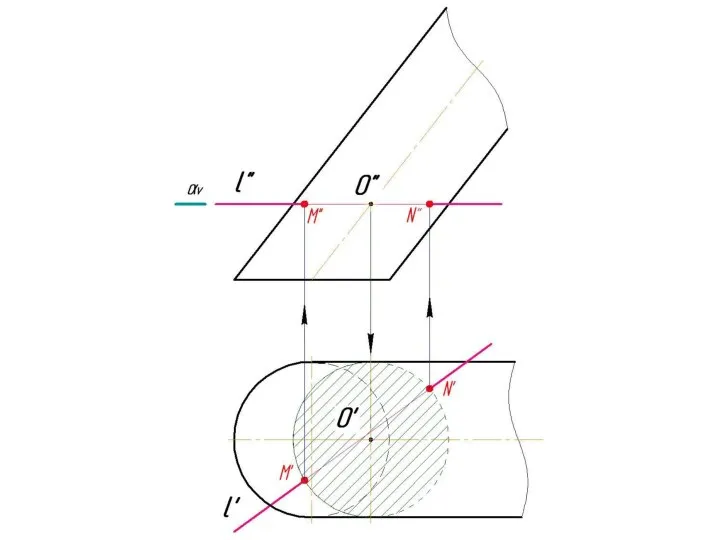
Слайд 4 Фронтально-проецирующая прямая l пересекает тор.
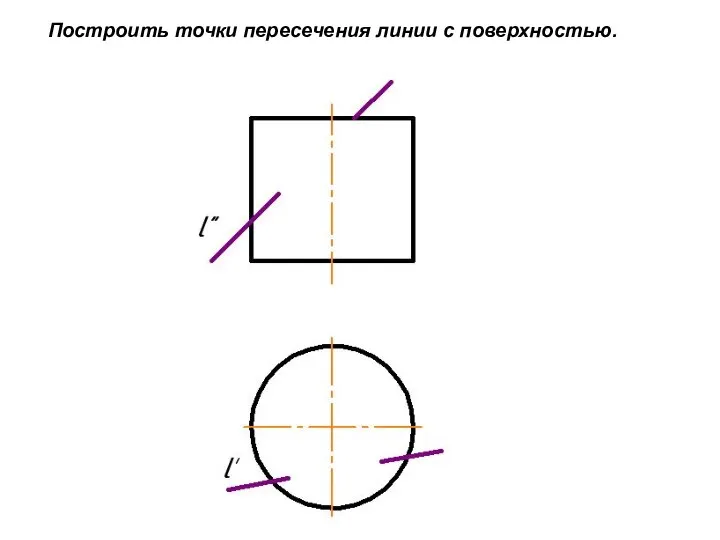
Слайд 11Построить точки пересечения линии с поверхностью.
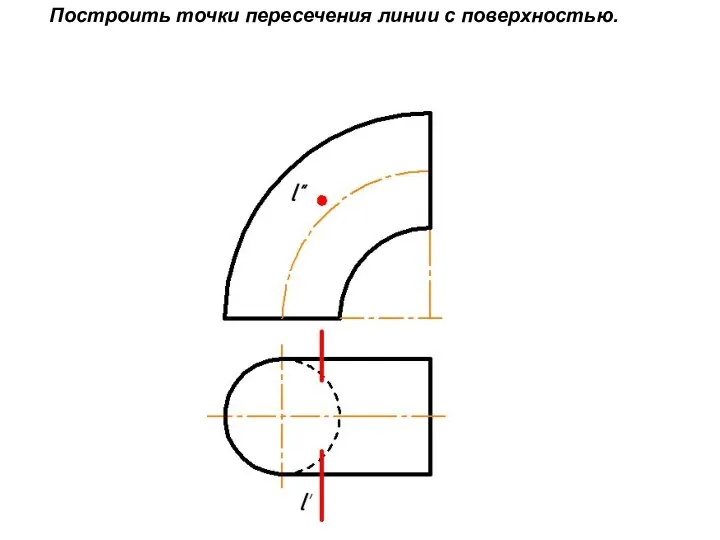
Слайд 15Построить точки пересечения линии с поверхностью.
Слайд 17Построить точки пересечения линии с поверхностью.
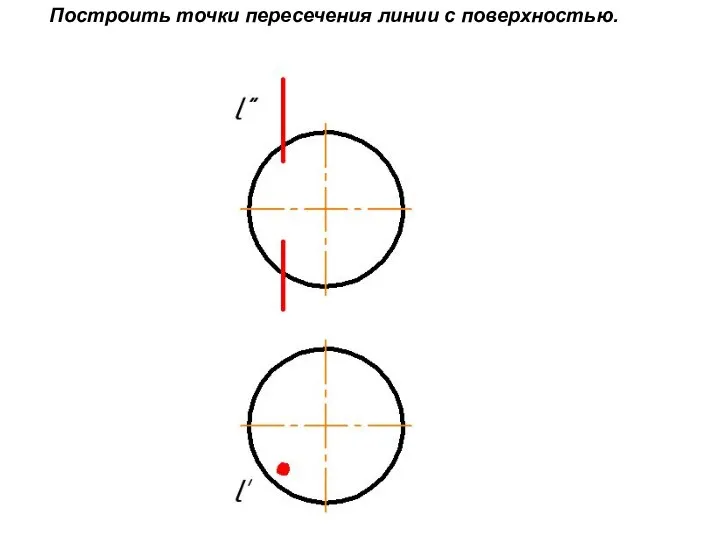
Слайд 26Построить точки
пересечения линии с
поверхностью.
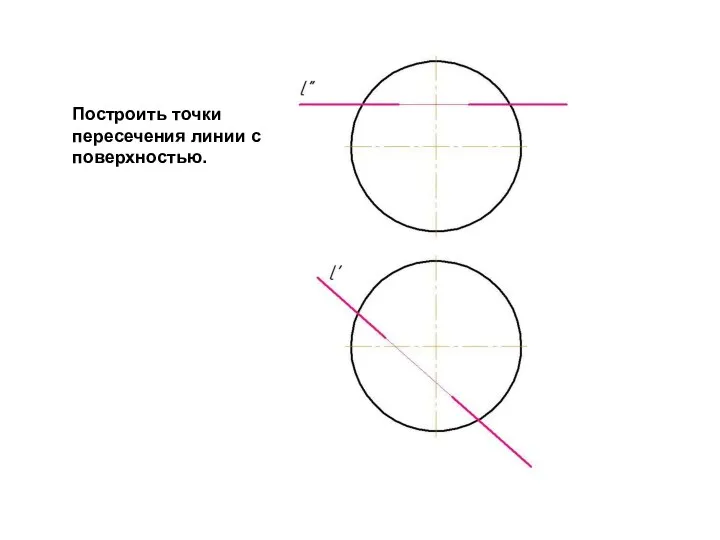
Слайд 31Построить точки пересечения линии с поверхностью.
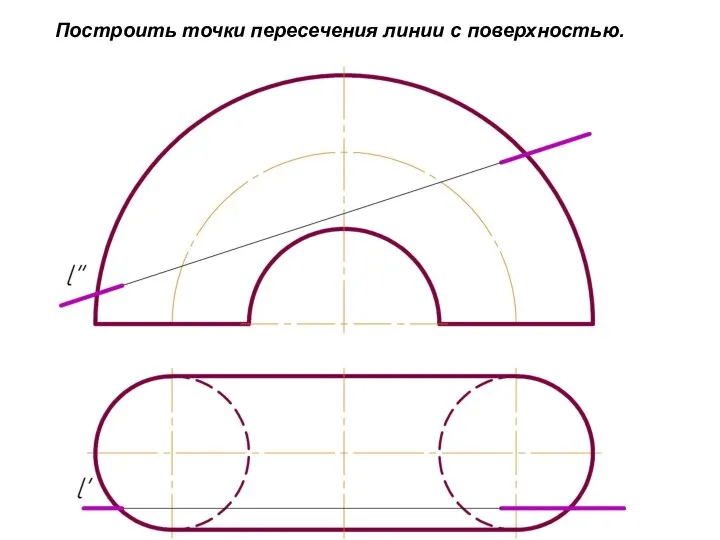
Слайд 39Построить точки
пересечения линии с
поверхностью.










 Формулы сложения
Формулы сложения Углы, связанные с окружностью
Углы, связанные с окружностью Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений
Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс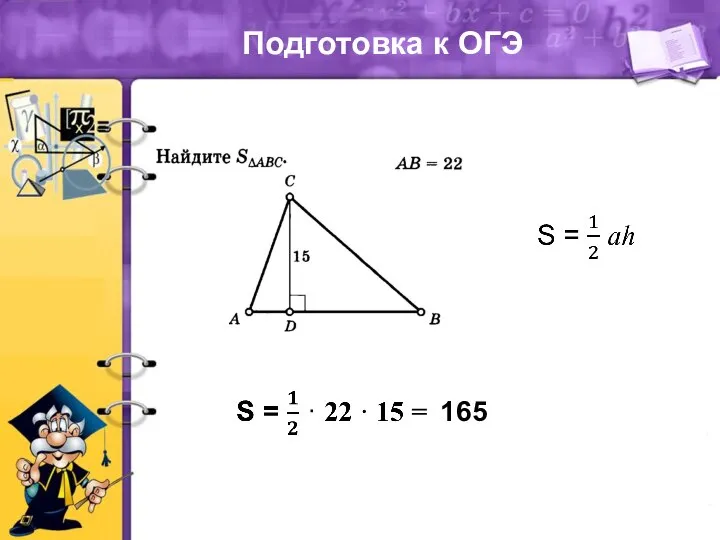 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Пирамиды. Правильная пирамида
Пирамиды. Правильная пирамида Степень с отрицательным показателем
Степень с отрицательным показателем Математические записи и схемы
Математические записи и схемы Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Применение производной к построению графиков функции
Применение производной к построению графиков функции Линейные алгоритмы
Линейные алгоритмы Стереометрия. Базовые понятия. Определения
Стереометрия. Базовые понятия. Определения Презентация на тему Системы линейных уравнений с двумя переменными
Презентация на тему Системы линейных уравнений с двумя переменными  Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Иррациональные неравенства
Иррациональные неравенства Генерация k-элементных подмножеств
Генерация k-элементных подмножеств Урок с применением ИКТ Они были первыми
Урок с применением ИКТ Они были первыми Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Математический хоккей
Математический хоккей Математический диктант
Математический диктант Задачи на пропорцию
Задачи на пропорцию Числовые последовательности
Числовые последовательности Угол между векторами
Угол между векторами Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Влияние коэффициентов линейной функции на ее график
Влияние коэффициентов линейной функции на ее график Дроби. Тест
Дроби. Тест