Содержание
- 2. Алгоритм вычисления вектора Ф, основанный на минимизации функционала, связанного с физическим смыслом решаемой задачи. Этап 1.
- 3. Этап 2. Подстановка аппроксимирующего выражения и вычисление производных по формулам вида Этап 3. Минимизация по вектору
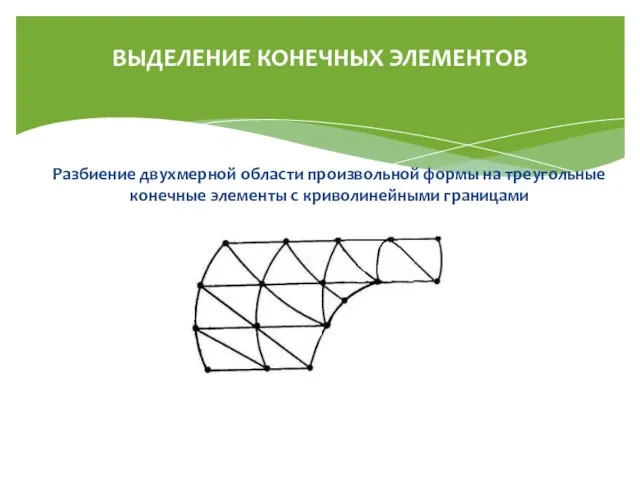
- 4. Разбиение двухмерной области произвольной формы на треугольные конечные элементы с криволинейными границами ВЫДЕЛЕНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
- 5. Порядок нумерации имеет в данном случае существенное значение, так как влияет на эффективность последующих вычислений. Матрица
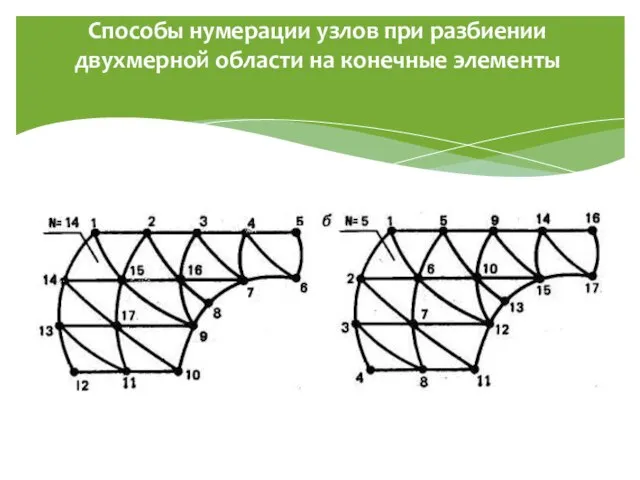
- 6. Способы нумерации узлов при разбиении двухмерной области на конечные элементы
- 7. ТОПОЛОГИЧЕСКАЯ ИНФОРМАЦИЯ тип конечного элемента; его порядковый номер; номера узлов элемента; координаты узлов, информацию о соединении
- 8. Алгоритм работы препроцессора Этап 1. Нанесение на заданную область некоторого множества узлов. Этап 2. Формирование узловых
- 9. Алгоритм разбиения области произвольной формы на треугольные конечные элементы Этап 1. Аппроксимация границы области совокупностью отрезков,
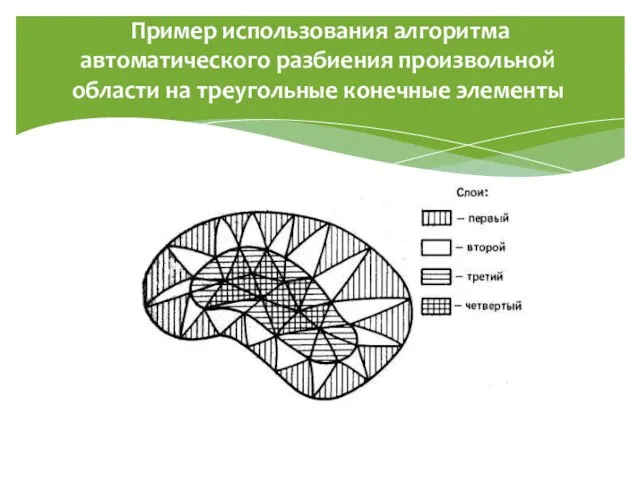
- 10. Пример использования алгоритма автоматического разбиения произвольной области на треугольные конечные элементы
- 11. Алгоритм разбиения области на элементы Определение граничных узлов области. Построение регулярной сетки с тем же числом
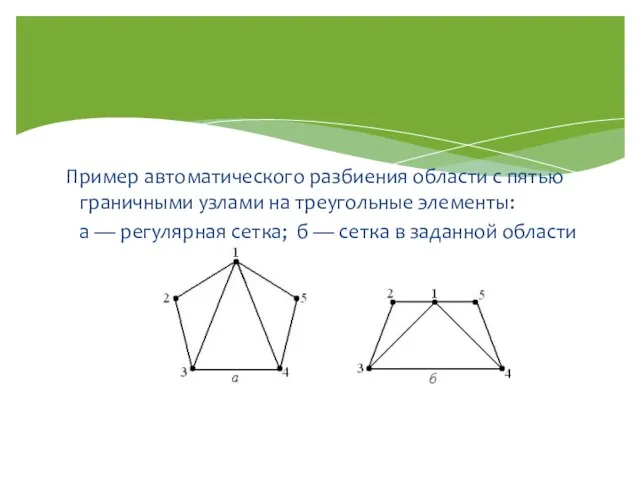
- 12. Пример автоматического разбиения области с пятью граничными узлами на треугольные элементы: а — регулярная сетка; б
- 13. Алгоритм построения регулярной сетки Окружение исходной точки кольцом равносторонних треугольников так, чтобы число внешних узлов было
- 15. Скачать презентацию








 Прибавить и вычесть 2
Прибавить и вычесть 2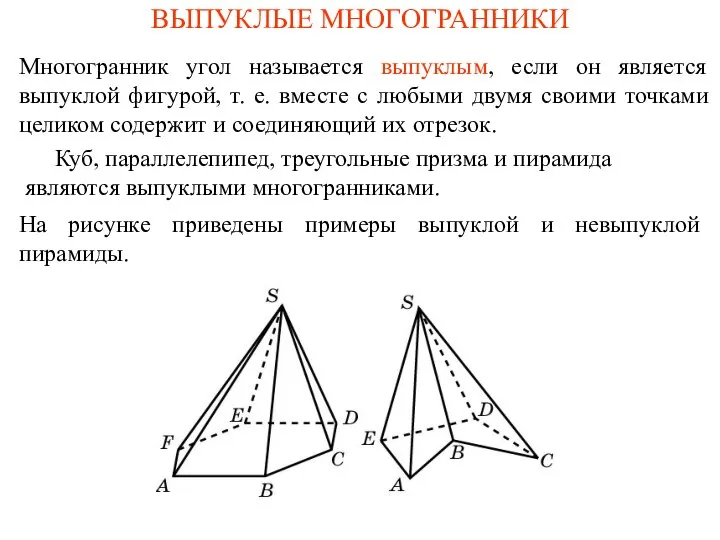 Выпуклые многогранники
Выпуклые многогранники Устное решение квадратных уравнений
Устное решение квадратных уравнений Зачем нужна математика
Зачем нужна математика Первообразная
Первообразная Ряды. Введение в математический анализ
Ряды. Введение в математический анализ Приёмы умножения числа 2
Приёмы умножения числа 2 Правило двух решений. Подход Неймана-Пирсона
Правило двух решений. Подход Неймана-Пирсона Первый признак параллельности прямых
Первый признак параллельности прямых Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Применение теоремы Пифагора при решении задач
Применение теоремы Пифагора при решении задач Считаем без ошибок. Задания для устного счёта
Считаем без ошибок. Задания для устного счёта Системы линейных алгебраических уравнений. Практикум
Системы линейных алгебраических уравнений. Практикум Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Тренажёр Яблоки по теме Сложение с переходом через десяток. 1 класс
Тренажёр Яблоки по теме Сложение с переходом через десяток. 1 класс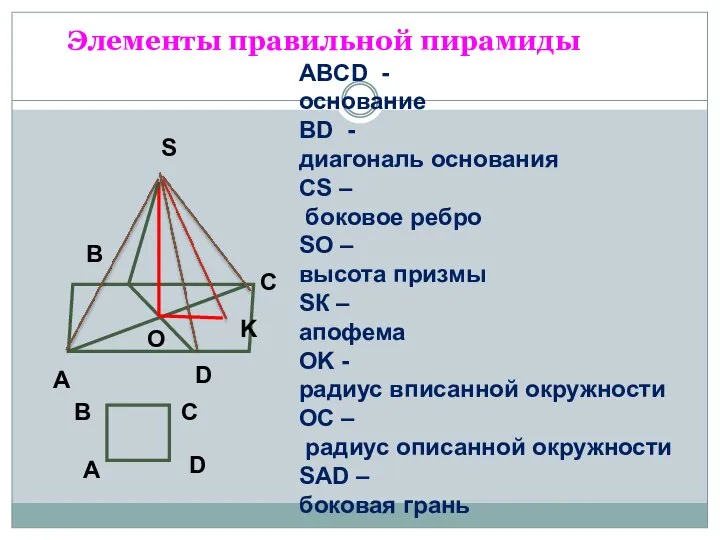 Правильная пирамида
Правильная пирамида Отрицательные числа в географии
Отрицательные числа в географии Векторы. Сложение и вычитание векторов
Векторы. Сложение и вычитание векторов Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Цифры (дойти до апельсина)
Цифры (дойти до апельсина)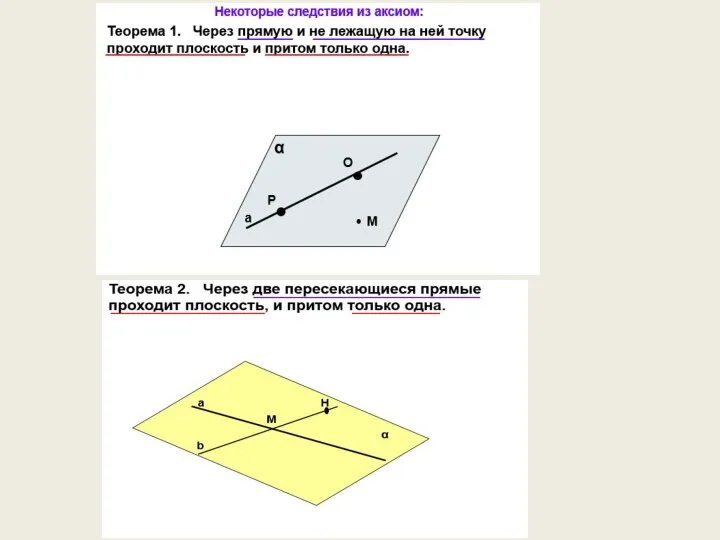 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Число и цифра 2
Число и цифра 2 Блок - схемы алгоритмов
Блок - схемы алгоритмов Доказательство неравенств. Решение задач на доказательство неравенств
Доказательство неравенств. Решение задач на доказательство неравенств Свойства степени
Свойства степени Нетрадиционные пособия по математическому развитию дошкольников (работа муниципального методического объединения воспитателей)
Нетрадиционные пособия по математическому развитию дошкольников (работа муниципального методического объединения воспитателей) Формулы двойного аргумента
Формулы двойного аргумента