Равнобедренный треугольник

Теоретический тест:
1. Медиана в равнобедренном треугольнике является биссектрисой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный; б) все его углы равны;
в) любая его высота является биссектрисой и медианой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно; б) может быть верно; в) всегда неверно.
5. Если треугольник равнобедренный, то:
а) он равносторонний; б) любая его медиана является биссектрисой и высотой; в) ответы а и б неверны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом; б) в равнобедренном; в) в равностороннем.

4
В
А
С
М
3
1
2
Дано: ∆АВС, АМ – медиана
АМ = МВ = МС
Доказать: ∠А = ∠В + ∠С
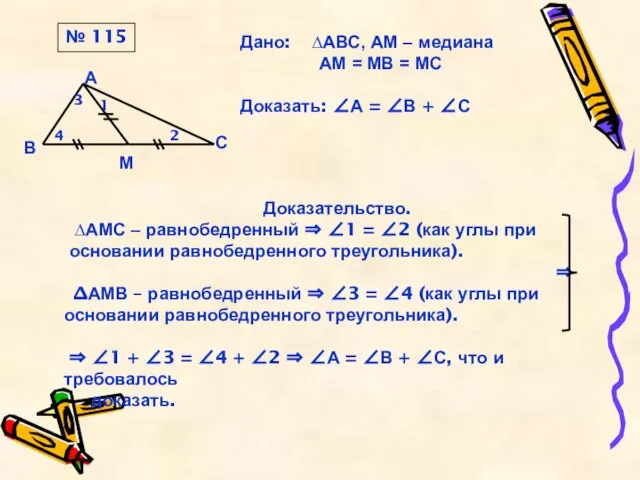
Доказательство.
∆АМС – равнобедренный ⇒ ∠1 = ∠2 (как углы при
основании равнобедренного треугольника).
⇒
∆АМВ – равнобедренный ⇒ ∠3 = ∠4 (как углы при
основании равнобедренного треугольника).
⇒ ∠1 + ∠3 = ∠4 + ∠2 ⇒ ∠А = ∠В + ∠С, что и требовалось
доказать.
№ 115

Дано: ∆АВС – равнобедренный
АС – основание
ВD – медиана
Е ∊ АВ, F ∊ СВ
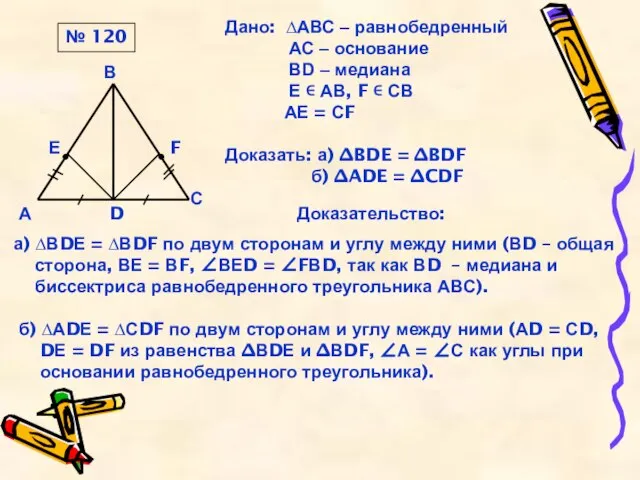
АЕ = СF
Доказать: а) ∆BDE = ∆BDF
б) ∆ADE = ∆CDF
№ 120
А
В
Е
F
С
D
а) ∆ВDЕ = ∆ВDF по двум сторонам и углу между ними (ВD – общая
сторона, ВЕ = ВF, ∠ВЕD = ∠FВD, так как ВD – медиана и
биссектриса равнобедренного треугольника АВС).
Доказательство:
б) ∆АDЕ = ∆СDF по двум сторонам и углу между ними (АD = СD,
DЕ = DF из равенства ∆ВDЕ и ∆ВDF, ∠А = ∠С как углы при
основании равнобедренного треугольника).

Самостоятельная работа
1.
1.
В
D
С
А
2.
2.
В
О
С
А
Дано: AD = CD
AC ⊥ BD
Доказать:
∆АВС – р/б
Дано:∆АВС – р/б
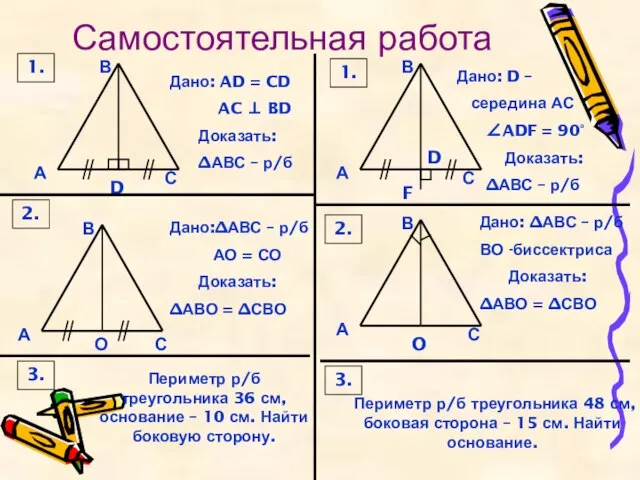
АО = СО
Доказать:
∆АВО = ∆СВО
3.
Периметр р/б треугольника 36 см, основание – 10 см. Найти боковую сторону.
3.
Периметр р/б треугольника 48 см, боковая сторона – 15 см. Найти основание.
В
С
А
D
F
Дано: D –
середина АС
∠ADF = 90°
Доказать:
∆АВС – р/б
В
С
А
O
Дано: ∆АВС – р/б
ВО -биссектриса
Доказать:
∆АВО = ∆СВО

Самостоятельная работа
1.
1.
В
D
С
А
Дано: AD = CD
AC ⊥ BD
Доказать:
∆АВС – р/б
В
С
А
D
F
Дано: D –
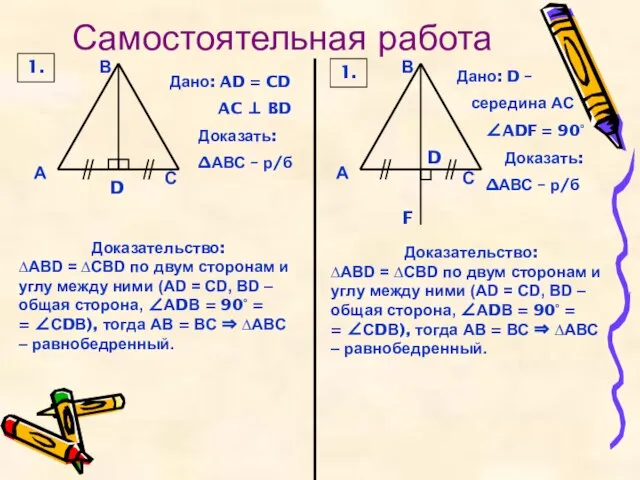
середина АС
∠ADF = 90°
Доказать:
∆АВС – р/б
Доказательство:
∆ABD = ∆CBD по двум сторонам и углу между ними (АD = СD, ВD – общая сторона, ∠АDВ = 90° =
= ∠СDВ), тогда АВ = ВС ⇒ ∆АВС – равнобедренный.
Доказательство:
∆ABD = ∆CBD по двум сторонам и углу между ними (АD = СD, ВD – общая сторона, ∠АDВ = 90° =
= ∠СDВ), тогда АВ = ВС ⇒ ∆АВС – равнобедренный.

2.
2.
В
С
А
Дано:∆АВС – р/б
АО = СО
Доказать:
∆АВО = ∆СВО
В
С
А
O
Дано:∆АВС – р/б
ВО -биссектриса
Доказать:
∆АВО = ∆СВО
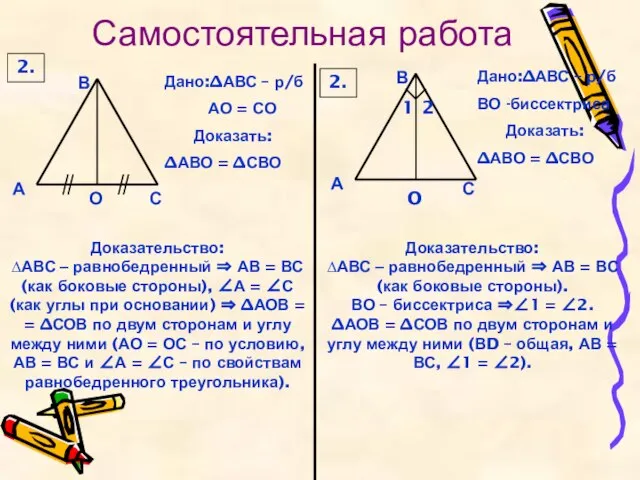
Самостоятельная работа
Доказательство:
∆АВС – равнобедренный ⇒ АВ = ВС (как боковые стороны), ∠А = ∠С (как углы при основании) ⇒ ∆АОВ =
= ∆СОВ по двум сторонам и углу между ними (АО = ОС – по условию, АВ = ВС и ∠А = ∠С – по свойствам равнобедренного треугольника).
О
Доказательство:
∆АВС – равнобедренный ⇒ АВ = ВС (как боковые стороны).
ВО – биссектриса ⇒∠1 = ∠2.
∆АОВ = ∆СОВ по двум сторонам и углу между ними (ВD – общая, АВ = ВС, ∠1 = ∠2).
2
1

Самостоятельная работа
3.
3.
Решение:
∆ABС – равнобедренный ⇒ АВ= ВС
РАВС=АВ+ВС+АС=АВ+ВС+10 = 36 ⇒ АВ + ВС = 36 – 10 = 26 см ⇒
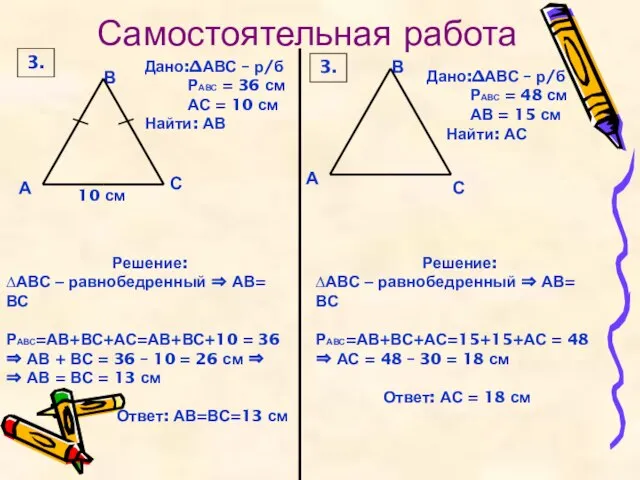
⇒ АВ = ВС = 13 см
Ответ: АВ=ВС=13 см
В
С
А
В
С
А
Дано:∆АВС – р/б
РАВС = 36 см
АС = 10 см
Найти: АВ
10 см
Решение:
∆ABС – равнобедренный ⇒ АВ= ВС
РАВС=АВ+ВС+АС=15+15+АС = 48 ⇒ АС = 48 – 30 = 18 см
Ответ: АС = 18 см
Дано:∆АВС – р/б
РАВС = 48 см
АВ = 15 см
Найти: АС

Дополнительные задачи.
А
В
С
D
1
2
Дано: АВ = ВС, ∠1 = ∠2
Доказать: ∆АDC – р/б
Дано: АВ = ВС, ∠1 = ∠2
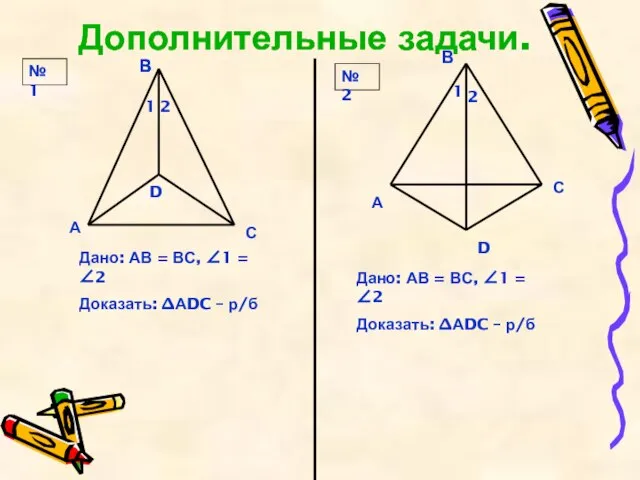
Доказать: ∆АDC – р/б
А
Дополнительные задачи.
В
В
С
D
1
2
№ 1
№ 2

Дополнительные задачи.
№ 4
№ 3
Периметр равнобедренного треугольника равен 37 см. Основание меньше боковой стороны на 5 см. Найдите стороны треугольника.
Периметр равнобедренного треугольника равен 45 см. Боковая сторона меньше основания на 3 см. Найдите стороны треугольника.