0; i < n; i++) {
polynome s = {
(-2*x[i]*pow(x[i+1],2)+h*pow(x[i+1],2))/pow(h,3)*f[i]+
(2*x[i+1]*pow(x[i],2)+h*pow(x[i],2))/pow(h,3)*f[i+1]+
(x[i]*pow(x[i+1],2))/pow(h,2)*m[i]+
(x[i+1]*pow(x[i],2))/pow(h,2)*m[i+1],
(2*pow(x[i+1],2)+4*x[i]*x[i+1]-2*x[i+1]*h)/pow(h,3)*f[i]+
(-4*x[i]*x[i+1]-2*x[i]*h-2*pow(x[i],2))/pow(h,3)*f[i+1]+
(pow(x[i+1],2)+2*x[i]*x[i+1])/pow(h,2)*m[i]+
(2*x[i]*x[i+1]+pow(x[i],2))/pow(h,2)*m[i+1],
(-4*x[i+1]-2*x[i]+h)/pow(h,3)*f[i]+
(4*x[i]+2*x[i+1]+h)/pow(h,3)*f[i+1]+
(-2*x[i+1]-x[i])/pow(h,2)*m[i]+
(-2*x[i]-x[i+1])/pow(h,2)*m[i+1],
2/pow(h,3)*f[i]-
2/pow(h,3)*f[i+1]+
1/pow(h,2)*m[i]+
1/pow(h,2)*m[i+1],
};
double check = (s[3]*(pow(x[i],3)+pow(x[i+1],3))+
s[2]*(pow(x[i],2)+pow(x[i+1],2))+
s[1]*(x[i]+x[i+1]))/2+s[0];
s[0] -= (check-(f[i]+f[i+1])/2);
printf("x ∈ [%lf, %lf], S3(x) = (%lf)x^3 + (%lf)x^2 + (%lf)x +(%lf)\n",
x[i],x[i+1], s[3],s[2],s[1],s[0]
);
}
}
Назаров Максим Вячеславович






![Программа m.push_back((4*f[1]-f[2]-3*f[0])/(2*h)); for (int i = 1; i m.push_back((f[i+1]-f[i-1])/(2*h)); m.push_back((3*f[n]-f[n-2]-3*f[n-1])/(2*h)); for (int](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/903106/slide-7.jpg)




 Пифагор и его теорема
Пифагор и его теорема Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики Расстояние от точки до плоскости
Расстояние от точки до плоскости Измеряй и сравнивай
Измеряй и сравнивай Задачи(БД)
Задачи(БД) Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов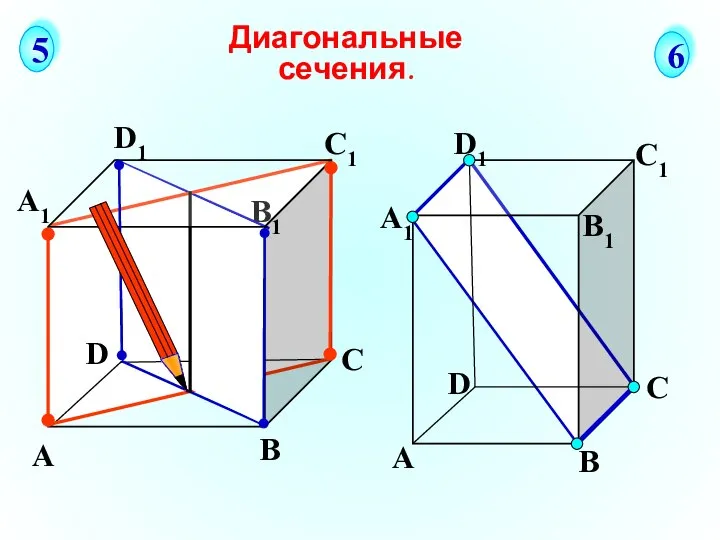 Диагональные сечения
Диагональные сечения Наибольшее и наименьшее значение функции. Примеры
Наибольшее и наименьшее значение функции. Примеры Квадратные уравнения. Основные понятия
Квадратные уравнения. Основные понятия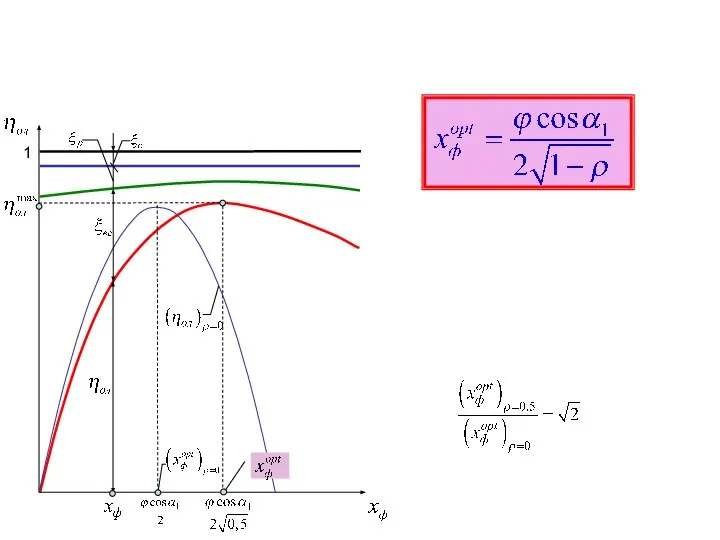 Оптимальный располагаемый теплоперепад ступени
Оптимальный располагаемый теплоперепад ступени Презентация на тему Методы решения тригонометрических уравнений (10 класс)
Презентация на тему Методы решения тригонометрических уравнений (10 класс)  Среднее арифметическое. Урок №2
Среднее арифметическое. Урок №2 Взаимно обратные числа
Взаимно обратные числа Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Страна Математика
Страна Математика Презентация на тему Рациональные числа и действия над ними
Презентация на тему Рациональные числа и действия над ними  Типовые дискретные последовательности
Типовые дискретные последовательности Длина. Сантиметр
Длина. Сантиметр Основные распределения математической статистики
Основные распределения математической статистики Кратные чисел. 5 класс
Кратные чисел. 5 класс Вычисление определенных интегралов с помощью неопределенных
Вычисление определенных интегралов с помощью неопределенных Числовые и буквенные выражения. Классная работа
Числовые и буквенные выражения. Классная работа Способы решения квадратных уравнений
Способы решения квадратных уравнений Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Логика
Логика повторение 7-9
повторение 7-9 Решаем задачи
Решаем задачи