Содержание
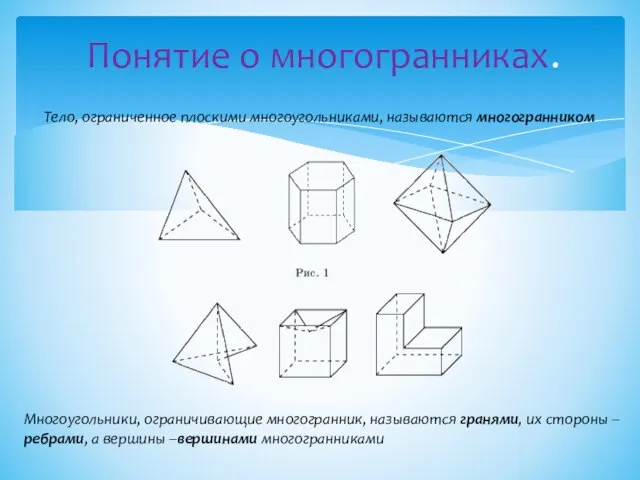
- 2. Понятие о многогранниках. Тело, ограниченное плоскими многоугольниками, называются многогранником Многоугольники, ограничивающие многогранник, называются гранями, их стороны
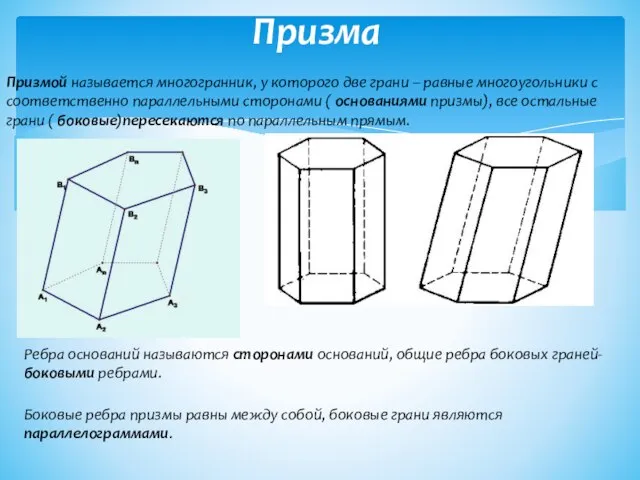
- 3. Призма Призмой называется многогранник, у которого две грани – равные многоугольники с соответственно параллельными сторонами (
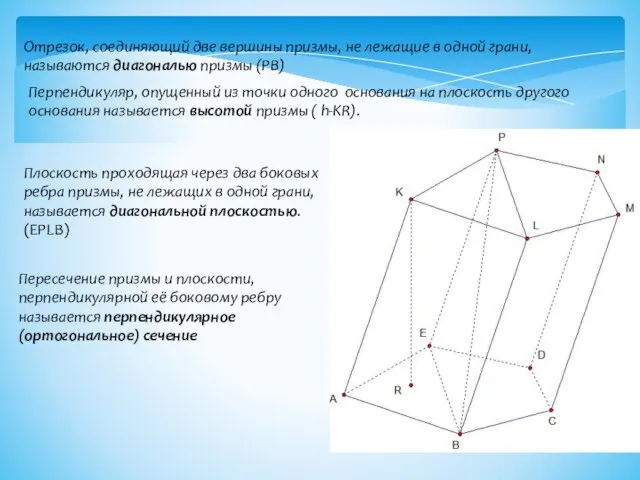
- 4. Отрезок, соединяющий две вершины призмы, не лежащие в одной грани, называются диагональю призмы (PB) Перпендикуляр, опущенный
- 5. Свойства призмы 1. Боковые ребра призмы параллельны и равны. 2. Перпендикулярное сечение перпендикулярно ко всем боковым
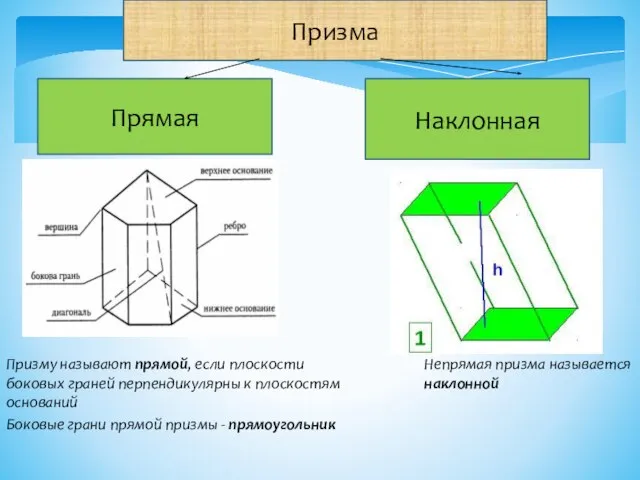
- 6. Призма Прямая Наклонная Призму называют прямой, если плоскости боковых граней перпендикулярны к плоскостям оснований Непрямая призма
- 7. Прямую призму называют правильной, если основанием её служит правильный многоугольник
- 8. Параллелепипед. Призма, основанием которой является параллелограммы ( их у него шесть), называется параллелепипедом . Грани параллелепипеда,
- 9. Типы параллелепипеда Прямоугольный параллелепипед — объёмная фигура, у которой шесть граней, и каждая из них является
- 10. Куб Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты Квадрат
- 11. Площади призмы где Росн- периметр основания, l-ребро призмы
- 13. Решение задач по теме: «Призма и его виды»
- 14. Дано: А1А2А3А4-прямоугольник А1А4=5, А3А4=4, А/3А3=6 Найти: А/2А4 Решение: По свойству имеем: (А/2А4)2= (А1А4 )2+ (А3А4)2 +
- 15. 1. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны: 1,1,2 2. Найдите диагональ прямоугольного параллелепипеда, если
- 16. Дано: А1А2А3А4-прямоугольник А1А4=5, А3А4=4, А/3А3=6 Найти: Sбок, Sполн. Решение:
- 17. Дано: А1А2А3 –призма, А1А2=13, А1А3=14, А3А2=15, Sполн =378 Найти: А/1А1 Решение:
- 20. Скачать презентацию













 Понятие функции
Понятие функции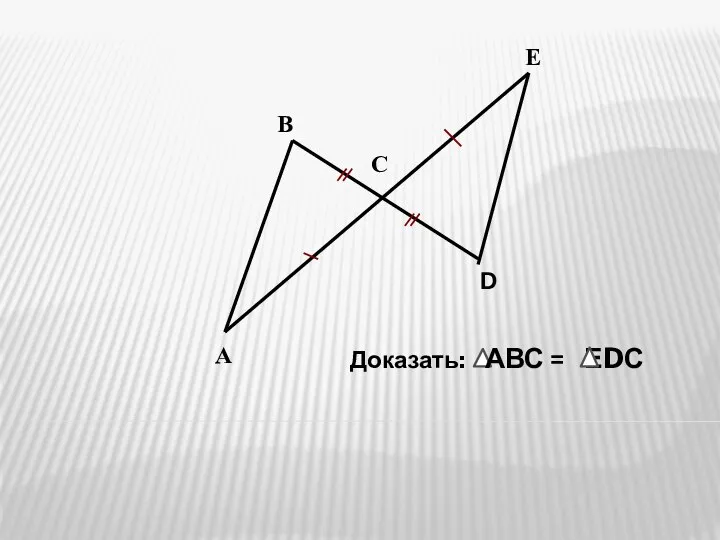 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач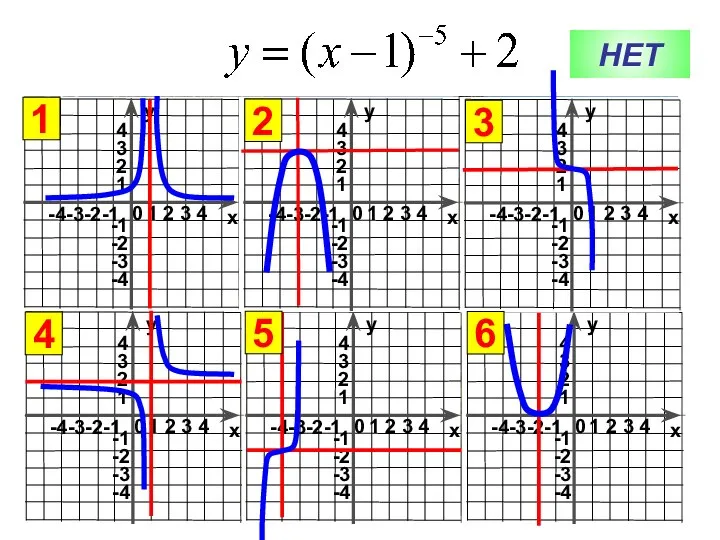 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого