Слайд 2Исходными и промежуточными данными, а также результатом работы алгоритмического процесса являются конструктивные

объекты
Слайд 3Конструктивный объект должен иметь:
Конечное множество элементов
2) Внутреннюю систему координат, позволяющую однозначно локализовать

любой его элемент
(второй элемент справа, элемент пятой строки и третьего столбца и т.д.)
Слайд 4Простейшим примером конструктивных объектов являются слова в некотором алфавите

Слайд 5Алфавитом называется непустое конечное множество
Элементы множества А называются буквами (символами)

Слайд 6Словом в алфавите А называется конечная последовательность
букв алфавита А. Натуральное число
n

≥ 0 называется длиной слова u.
Слайд 7В теории алгоритмов удобно считать, что

Слайд 8Слово нулевой длины называется пустым словом
Обозначение: Λ

Слайд 9Частными видами слов являются записи натуральных чисел, конечные десятичные дроби и т.п.
Пример
Алгоритм

α - сложение натуральных чисел
Р = 12 + 24
Q = 36
P и Q являются словами в алфавите A={0, 1, 2, …, 9, +}
Слайд 10Пример
Конструктивные объекты:
- Натуральные числа, записанные в какой-либо системе счисления
- Слова в естественном

языке
- Формулы алгебры высказываний
- Матрицы в их линейной записи:
Слайд 11Пример
Не конструктивные объекты:
- Действительное число, являющееся бесконечной десятичной дробью (например, число π

)
- Произвольная функция f(x): N → N
Слайд 12Всякий конструктивный объект можно однозначно и полностью закодировать в виде слова.
Т.о. слова

в алфавите – главный вид конструктивных объектов











 Определитель матрицы. Правило Крамера
Определитель матрицы. Правило Крамера Математика. Урок 4
Математика. Урок 4 Комбинаторика. Художественные стороны комбинаторики. Разработка декоративного модуля для комбинаторной композиции
Комбинаторика. Художественные стороны комбинаторики. Разработка декоративного модуля для комбинаторной композиции Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1 Комплексные числа и действия над ними
Комплексные числа и действия над ними Перпендикулярность плоскостей. Параллепипед
Перпендикулярность плоскостей. Параллепипед Специальные случайные распределения, используемые в математической статистике
Специальные случайные распределения, используемые в математической статистике Задачи на проценты
Задачи на проценты Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Презентация на тему Арифметическая прогрессия: практикум
Презентация на тему Арифметическая прогрессия: практикум  Подготовка к ВПР (8 класс)
Подготовка к ВПР (8 класс) Примеры решения неравенств
Примеры решения неравенств Поиск преступника. Решение логической задачи
Поиск преступника. Решение логической задачи Площадь многоугольника
Площадь многоугольника Криволинейные интегралы
Криволинейные интегралы Понятие вектора (9 класс)
Понятие вектора (9 класс)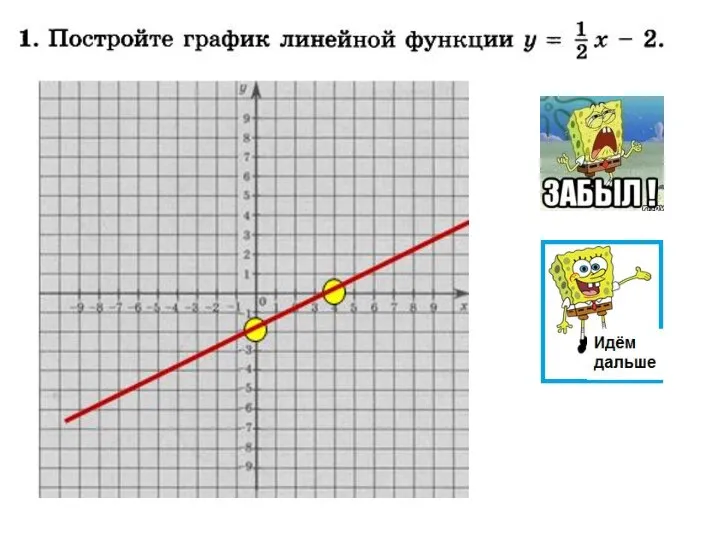 Линейная функция
Линейная функция Понятия и свойства функции. Предел функции. Теоремы о пределах. Нахождение пределов функций
Понятия и свойства функции. Предел функции. Теоремы о пределах. Нахождение пределов функций Реализация статистических методов оценки параметров динамической случайной величины
Реализация статистических методов оценки параметров динамической случайной величины Разные способы доказательства теоремы о сумме углов треугольника
Разные способы доказательства теоремы о сумме углов треугольника Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Упрощение логических выражений
Упрощение логических выражений Презентация на тему Преобразование выражений содержащих квадратные корни
Презентация на тему Преобразование выражений содержащих квадратные корни  Взаимное расположение прямой и окружности (7 класс)
Взаимное расположение прямой и окружности (7 класс) Платоновы и Архимедовы тела
Платоновы и Архимедовы тела Reshenie_sistem_logicheskikh_uravneniy_vse_metody
Reshenie_sistem_logicheskikh_uravneniy_vse_metody 04.17.21.00[1]
04.17.21.00[1] Уравнение и его корни
Уравнение и его корни