Показатели вариации

Показатели, применяемые для изучения статистической практики и науки, подразделяют на группы по следующим признакам:
1) по сущности изучаемых явлений – это объемные, характеризующие размеры процессов, и качественные, которые выражают количественные соотношения, типичные свойства изучаемых совокупностей;
2) по степени агрегирования явлений – это индивидуальные, которые характеризуют единичные процессы, и обобщающие, отображающие совокупность в целом или ее части;
3) в зависимости от характера изучаемых явлений – интервальные и моментные. Данные, отображающие развитие явлений за определенные периоды времени, называют интервальными показателями, т. е. это статистический показатель, который характеризуют процесс изменения признаков. К моментным показателям относят показатели, которые отражают состояние явления на определенную дату (момент);
4) в зависимости от пространственной определенности различают показатели: федеральные – характеризуют изучаемый объект в целом по стране; региональные и местные – эти показатели относятся к определенной части территории или отдельному объекту;
5) в зависимости от свойств конкретных объектов и формы выражений статистические показатели делятся на относительные, абсолютные и средние, данные показатели будут рассмотрены ниже.

Статистические данные, полученные при наблюдении, в результате сводки, группировки, почти всегда являются абсолютными величинами, т. е. величинами, которые выражены в натуральных единицах и получены в результате счета или непосредственного измерения. Абсолютные величины отражают численность единиц изучаемых совокупностей, размеры или уровни признаков зарегистрированных у отдельных единиц совокупности, и общий объем количественно выраженного признака как результат суммирования всех его отдельных значений.
Абсолютные величины по способу выражения размеров изучаемых процессов подразделяются на: индивидуальные и суммарные, они в свою очередь относятся к одному из видов обобщающих величин. Размеры количественных признаков у каждой статистической единицы характеризуют индивидуальные абсолютные величины, а также они являются базой при статистической сводке для соединения отдельных единиц статистического объекта в группы. На их основе получают абсолютные величины, в которых можно выделить показатели объема признаков совокупности и показатели численности совокупности. Если заняться исследованием развития торговли и ее состояния в определенном районе, то определенное количество фирм можно отнести к индивидуальным величинам, а объем товарооборота и число работников, работающих в фирме, относят к суммарным.
Абсолютные величины бывают экономически простыми (численность магазинов, работников) и экономически сложными (объем товарооборота, размер основных фондов).

Абсолютные величины – всегда числа именованные, имеют определенную размерность, единицы измерения. В статистической науке применяются натуральные, денежные (стоимостные) и трудовые единицы измерения.
Единицы измерения называют натуральными, если они будут соответствовать потребительским или природным свойствам предмета, товара и будут выражены в физических весах, мерах длины и т. п. В статистической практике натуральные единицы измерения могут быть составными. Применяют условно–натуральные единицы измерения при суммировании количества разнородных товаров, продуктов.
Трудовые единицы измерения (человеко–дни, человеко–часы) используются для определения затрат труда на производства продукции, выполнение работы и т.д.
Абсолютные величины измеряются в стоимостных единицах – ценах. В стоимостных единицах измеряют доходы населения, валовой выпуск продукции и др.

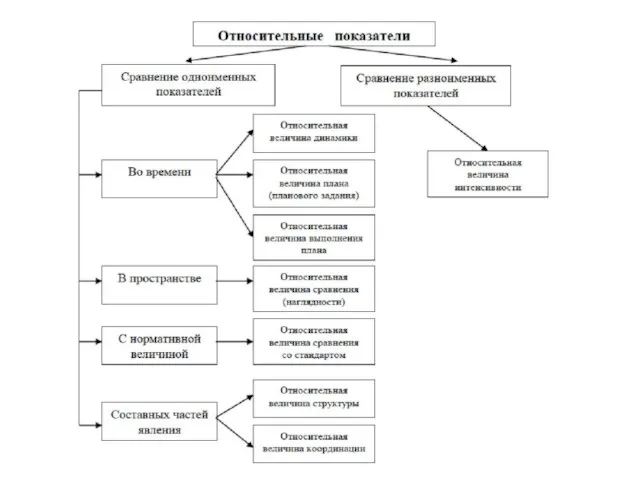
Показатели, полученные в результате сравнения абсолютных величин, в статистике называют относительными величинами.
Относительные величины дают представление, во сколько раз одна абсолютная величина больше другой или какую часть одна абсолютная величина составляет от другой, или сколько единиц одной совокупности приходится на единицу другой.
Относительные величины – это показатель, который представляет собой частное от деления двух статистических величин и характеризует количественное соотношение между ними.
Для расчета относительных величин в числитель ставится сравниваемый показатель, который будет отражать изучаемое явление а в знаменателе отражается показатель, с которым и будет производиться это сравнение, он является основанием или базой для сравнения. База сравнения – это своеобразный измеритель. Основание имеет результат отношения в зависимости от количественного (числового) значения, который выражается в: коэффициенте, процентах, промилле или децимилле.
Относительные величины, используемые в статистической практике:
относительная величина структуры;
относительная величина координации;
относительная величина планового задания;
относительная величина выполнения плана;
относительная величина динамики;
относительная величина сравнения;
относительная величина интенсивности.

Понятие о средней. Виды и способы исчисления.
Средняя величина – это обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Средняя – это сводная характеристика закономерностей процесса в тех или иных условиях, где протекает данный процесс.

Виды средних
1.Степенные средние.
2.Структурные средние.

Степенные средние
Степенные средние рассчитываются по единой формуле при различных степенях:
где - средняя величина; x – варианта; m – степень ; n – количество признаков.
Все средние величины делятся на :
а) Простые. Данные величины рассчитываются по не сгруппированной совокупности единиц.
б) Взвешенные. Показатель рассчитывается для сгруппированной совокупности.

Таблица 1 – Расчет степенных средних
где f – частота, т.е. число повторений единиц совокупности в каждой группе .

Правило мажорантности: Чем больше степень m , тем больше значение средней.
Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений отдельных признаков единиц совокупности.
Свойства средней арифметической величины:
Если все индивидуальные значения признака (варианты x ) уменьшить или увеличить на число а , то средняя величина увеличится или уменьшится на число а.
Если все варианты x увеличить или уменьшить в i раз, то средняя величина увеличится или уменьшится в i раз
Если все частоты f увеличить или уменьшить в k раз, то средняя величина не изменится.

В статистике для расчета средней арифметической величины с использованием данных свойств применяется расчет средней величины «способом момента».
Допустим, что все варианты x сначала уменьшат на одно и тоже число а , а потом уменьшат в i раз, то получится новый вариационный ряд распределения с новыми вариантами x’ :
Варианта x в интервальном ряду распределения рассчитывается как середина интервала:
Средняя величина для нового вариационного ряда будет рассчитываться как момент первого порядка:
Среднее для первоначального ряда будет рассчитываться:
где i – величина интервала; A –значение варианты, находящейся в середине вариационного ряда и имеющее наибольшую частоту. Если разложим ,то
Данный расчет средней применяется только в тех случаях, если данные сгруппированы и имеют равные интервалы.

Средняя гармоническая определяется в тех случаях, когда неизвестны те данные, которые необходимы для расчета средней арифметической величины.
Средняя гармоническая – это обратная величина средней арифметической.
Средняя геометрическая применяется в тех случаях, когда индивидуальное значение признака представлены в виде относительной величины динамики, построенной в виде цепных величин.
Средняя квадратическая и кубическая применяется если необходимо рассчитать среднюю, размер признака, которые выражены в квадратных или кубических единицах измерения.

Структурные средние
Применяются для изучения внутреннего строения и структуры изучаемого явления.
Мода – это наиболее часто встречающаяся величина в изучаемой совокупности. Прежде чем рассчитать моду, определяют модальный интервал (интервал с наибольшей частотой f ).
Расчет моды:
где - нижняя граница модального интервала;
- величина интервала
- частота модального интервала
- частота предшествующая модальной
- частота следующая за модальной

Медиана – величина, которая делит всю совокупность на 2 равные части, причем одна часть меньше медианы, а вторая часть совокупности больше медианы.
Медианный интервал – это интервал, в котором накопленная частота S превышает половину всех наблюдений (∑f/2). Накопленная частота S рассчитывается путем сложения каждой последующей частоты к предыдущей.
Расчет медианы:
Где - нижняя граница медианного интервала
- величина интервала
- накопленная частота предшествующая медианной
- частота медианного интервала

Квартиль – это величина , которая делит всю совокупность на 4 равные части. Различают нижний и верхний квартили.
Нижний квартиль ( ) показывает максимальную величину в минимальной группе, является ¼ всех наблюдений.
Нижний квартильный интервал – это интервал, в котором накопленная частота S превышает четвертую часть всех наблюдений (∑f/4). Нижний квартиль определяется по формуле:
Верхний квартиль( ) – это величина, которая является минимальной величиной в максимальной группе в совокупности, разбитой на четыре части.
Верхний квартильный интервал –это интервал, в котором накопленная частота S больше ¾ всех наблюдений (3∑f/4)

Квинтели – варианты, которые делят ряд на 5 равных частей. Расчет квинтелей производится также, как и медианы и квартилей. Так, нижний квинтель может быть вычислен по формуле:
Верхний квинтель будет рассчитан по формуле:

Децили – варианты, которые делят ряд на 10 равных частей. Вычисление децилей производится также, как и квинтелей. Так, нижний дециль будет рассчитан по формуле:
Верхний дециль будет выглядеть:

Показатели вариации
Вариация- это изменение величины либо значения признака при переходе от одной единицы совокупности к другой
Для характеристики вариации совокупности применяют показатели вариации. Чем больше варианты единицы совокупности различны между собой, тем больше они отличаются от своей средней и наоборот, поэтому нельзя ограничиваться расчетом только средней величины. Нужно рассчитывать показатели которые характеризуют отклонение каждого варианта от средней.

Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Относительные показатели вариации включают:
Коэффициент осцилляции
Относительное линейное отклонение (линейный коэффициент вариации)
Коэффициент вариации (относительное отклонение)

Размах вариации(R) - это разность между максимальным и минимальным значениями признака.
Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.
Формула расчета:

Среднее линейное отклонение— средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической (D)
для несгруппированных данных (простое)
для сгруппированных данных (взвешенное)
-варианты; - средняя величина; - кол-во признаков; -частота

Дисперсия — показывает среднюю площадь отклонений вариантов признака от их средней величины.
Она вычисляется по формуле:
Простая дисперсия для несгруппированных данных:
Взвешенная дисперсия для вариационного ряда
1)обычный способ
2) способ момента

Свойства дисперсии:
если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится;
если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия уменьшится или увеличится в i2 раз.

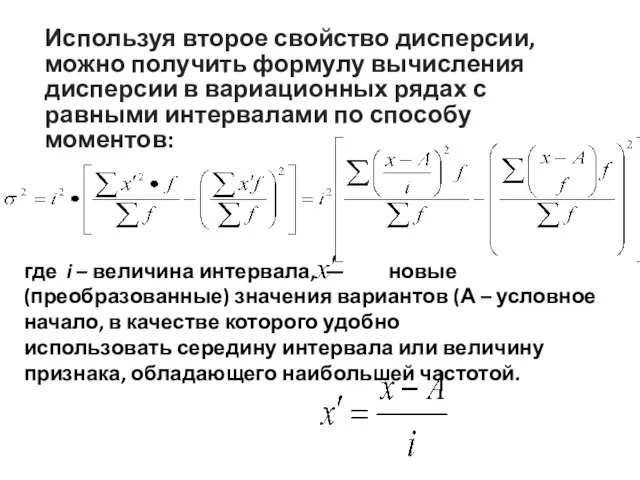
Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
где i – величина интервала, — новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.

Среднее квадратическое отклонение -
равно корню квадратному из дисперсии:
-для несгруппированных данных
-для сгруппированных данных
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от их среднего значения.

Среднее значение альтернативного признака
Среднее значение альтернативного признака:
Дисперсия альтернативного признака
Наличие признака=1, его отсутствие =0.
Р- доля единиц обладающих признаком
q-доля остальных единиц
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком.
Среднее квадратическое отклонение альтернативного признака:

Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.

Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% и наоборот.

Если данные представлены в виде аналитической группировки, в статистике рассматривают три вида дисперсии:
Общая дисперсия измеряет вариацию признака x во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию.
-общая средняя арифметическая всей совокупности
Межгрупповая дисперсия (факторная) объясняет вариацию, вызванную признаком, положенным в основу группировки.
Средняя из внутригрупповых дисперсия (остаточная) объясняет ту часть вариации, которая вызвана действием (влиянием) на признак x всех остальных признаков (факторов), кроме группировочного.
- средняя величина по отдельной группе

Правило сложения дисперсий
Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную.