Слайд 2Интегрирование через преобразование дифференциала

Слайд 5Метод замены переменной
Пример 2.2

Слайд 9Метод интегрирования по частям

Слайд 12Метод интегрирования рациональных дробей
Дробь является рациональной, если в числителе и в знаменателе

находятся многочлены.
Рациональная дробь является правильной, если степень числителя меньше степени знаменателя.
Рациональная дробь является неправильной, если степень числителя больше степени знаменателя.
Слайд 152. Разложим дробную часть на сумму простейших дробей, для этого знаменатель раскладываем


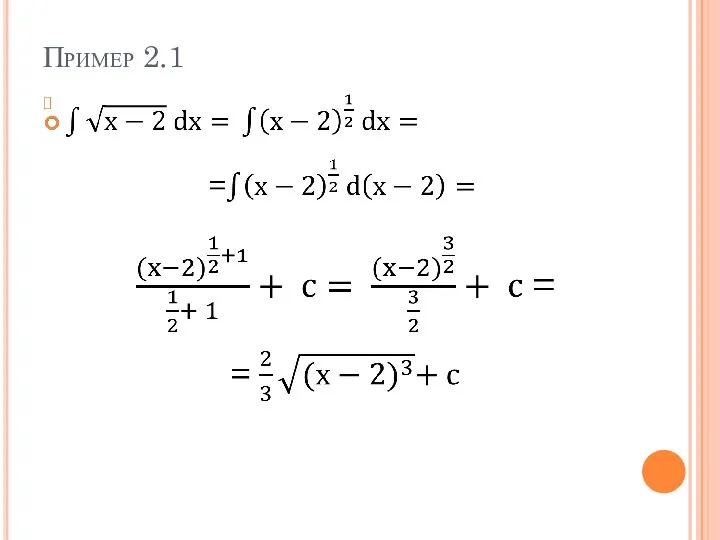
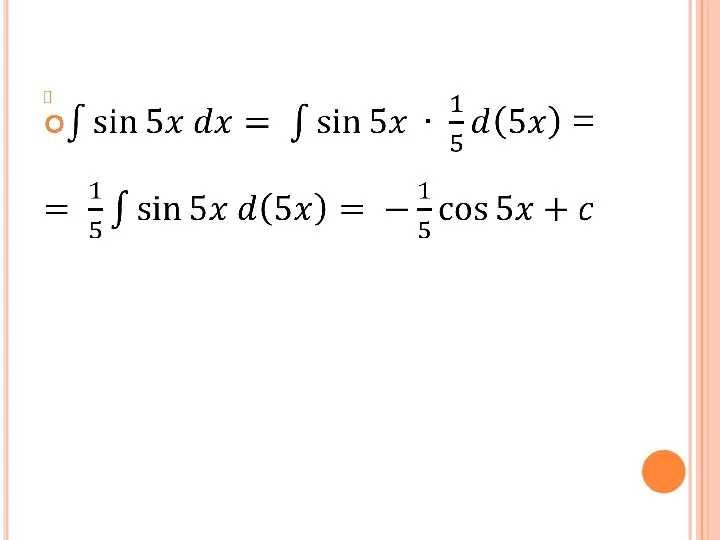

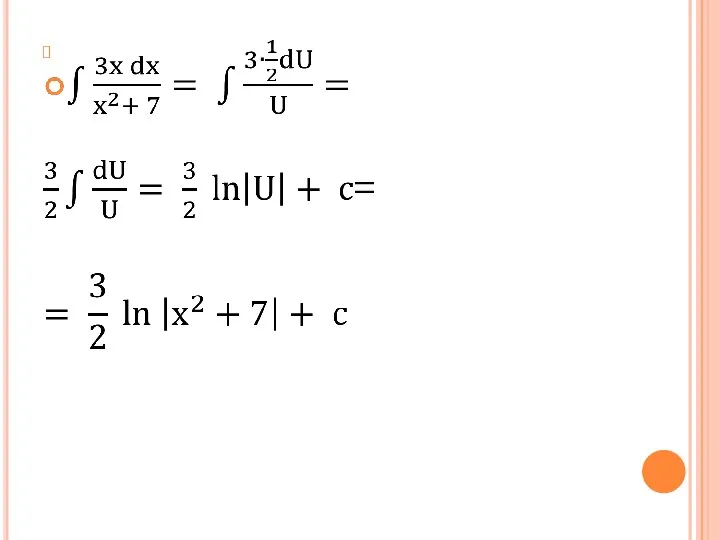
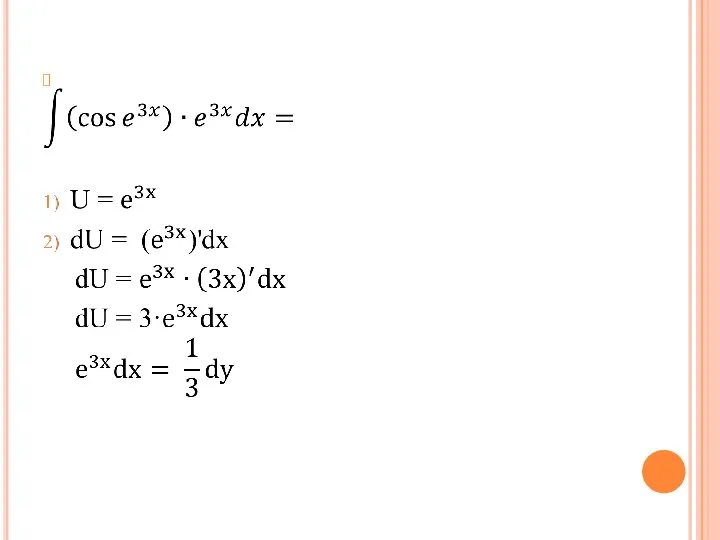
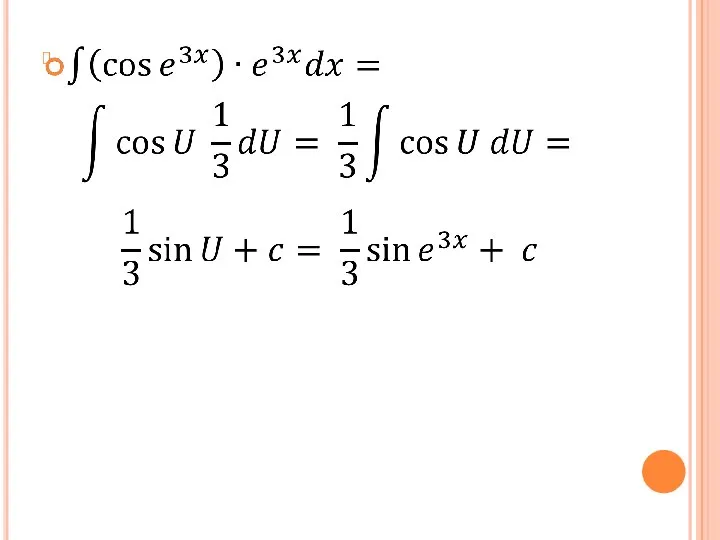

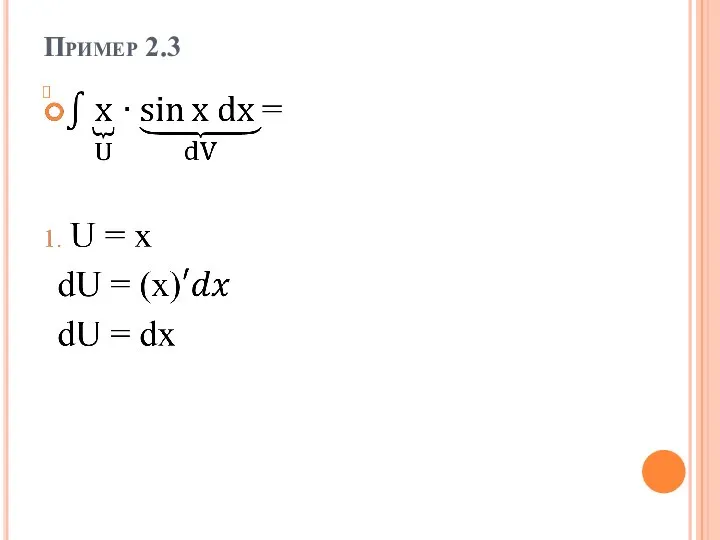
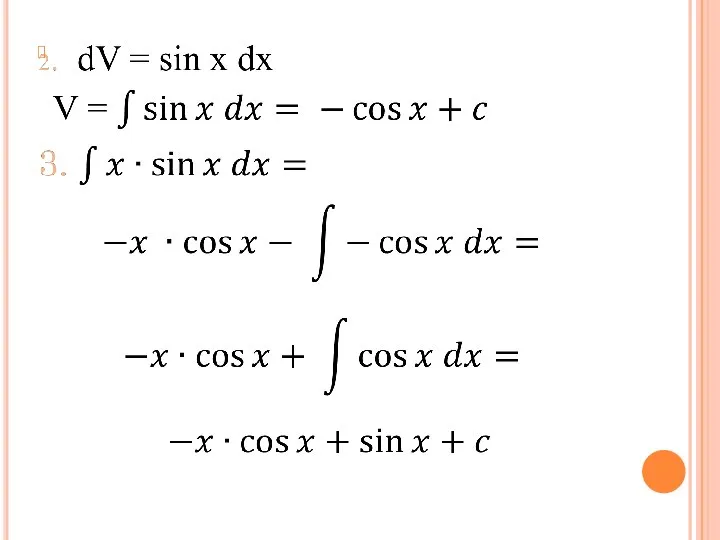


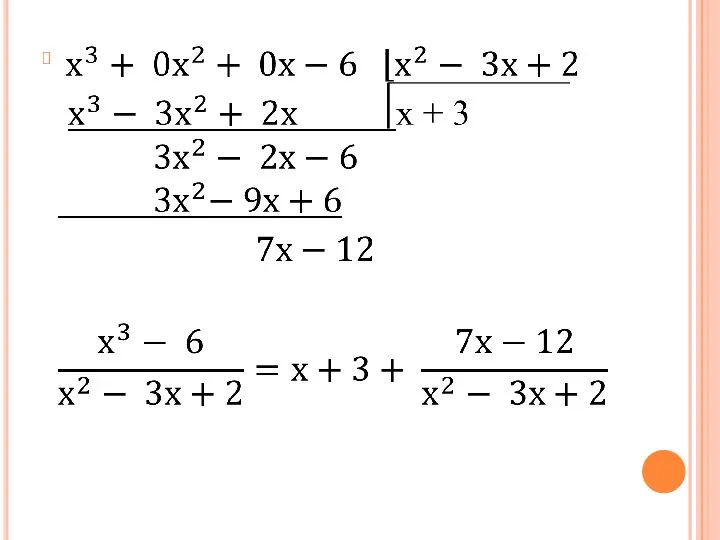

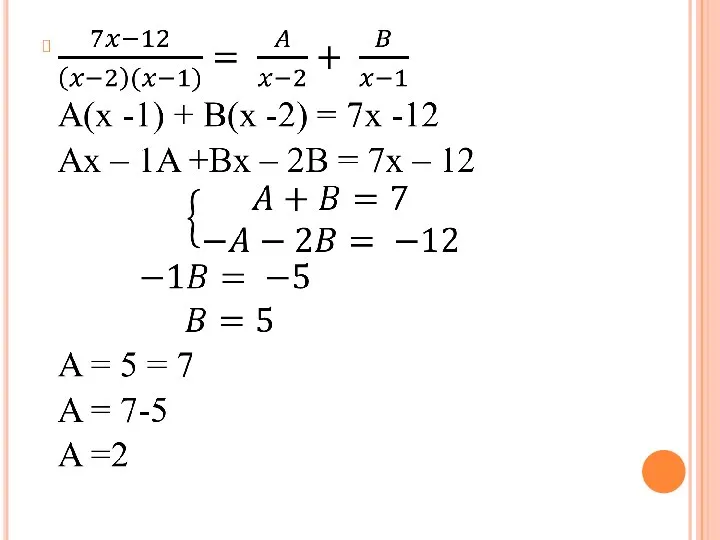
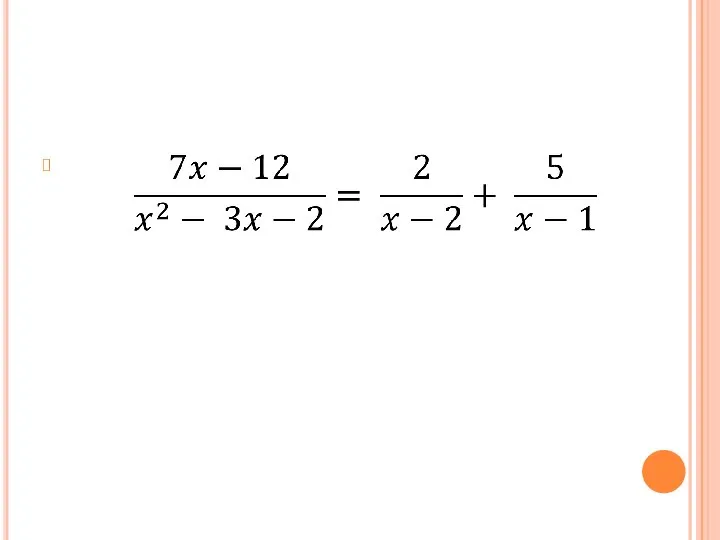
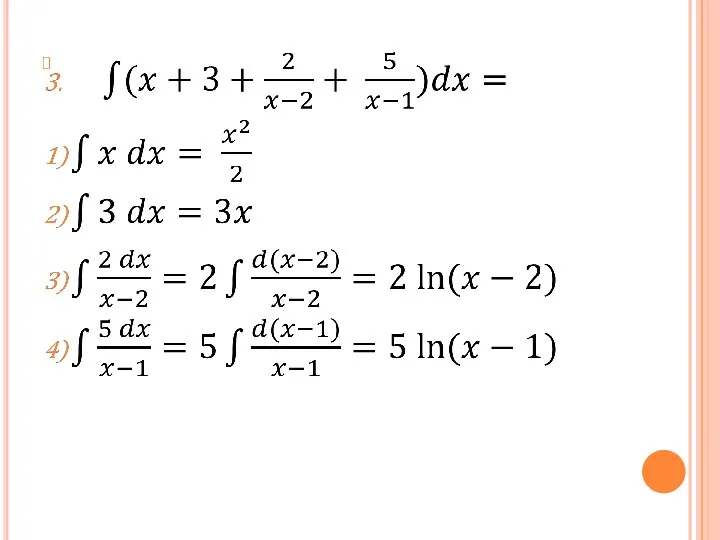
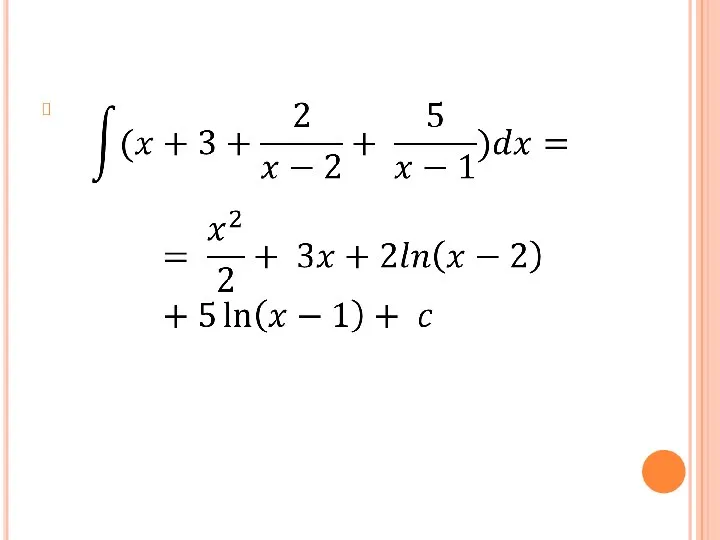
 Теорема Пифагора (часть 2)
Теорема Пифагора (часть 2) Интегрирование методом внесения под знак дифференциала
Интегрирование методом внесения под знак дифференциала Уравнение с двумя переменными
Уравнение с двумя переменными Презентация на тему Мир правильных многогранников
Презентация на тему Мир правильных многогранников  Примеры на 5
Примеры на 5 Тела и поверхности вращения
Тела и поверхности вращения Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Решение тригонометрических неравенств
Решение тригонометрических неравенств Презентация по математике "Мы рады привествовать вас на уроке математики" -
Презентация по математике "Мы рады привествовать вас на уроке математики" -  Решение составных задач
Решение составных задач Задачи на координатной плоскости
Задачи на координатной плоскости Система однородных линейных уравнений
Система однородных линейных уравнений Элементы векторной алгебры
Элементы векторной алгебры теорема Виета
теорема Виета Область определения функции. 9 класс
Область определения функции. 9 класс Площади четырехугольников
Площади четырехугольников Многогранники в нашей жизни
Многогранники в нашей жизни Деление целого на 2 части
Деление целого на 2 части Производная сложной функции. Исследование функции с помощью производной. Дифференциал
Производная сложной функции. Исследование функции с помощью производной. Дифференциал Кривая производственных возможностей
Кривая производственных возможностей Призма и ее виды. Чертеж призмы
Призма и ее виды. Чертеж призмы Презентация на тему Километр (3 класс)
Презентация на тему Километр (3 класс)  Самостоятельная работа по геометрии. 8 класс
Самостоятельная работа по геометрии. 8 класс Квадратные уравнения. Подготовка к контрольной работе. 8 класс
Квадратные уравнения. Подготовка к контрольной работе. 8 класс Векторы
Векторы Построение сечений
Построение сечений Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер Отрезки (Начало)
Отрезки (Начало)