Базель, в Швейцарии. У Леонарда было две младшие сестры – Анна Мария и Мария Магдалена. После рождения Эйлера, семья переезжает в городок Риен.
Отец мальчика был другом Иоганна Бернулли – известного европейского математика, оказавшего большое влияние на Леонарда. В тринадцать лет Эйлер-младший поступает в Базельский университет, и в 1723 г. получает степень магистра философии. В своей диссертации Эйлер сравнивает философии Ньютона и Декарта. Иоганн Бернулли, дававший мальчику по субботам частные уроки, быстро распознаёт выдающиеся способности мальчика к математике и убеждает его оставить раннюю теологию и сосредоточиться на математике.
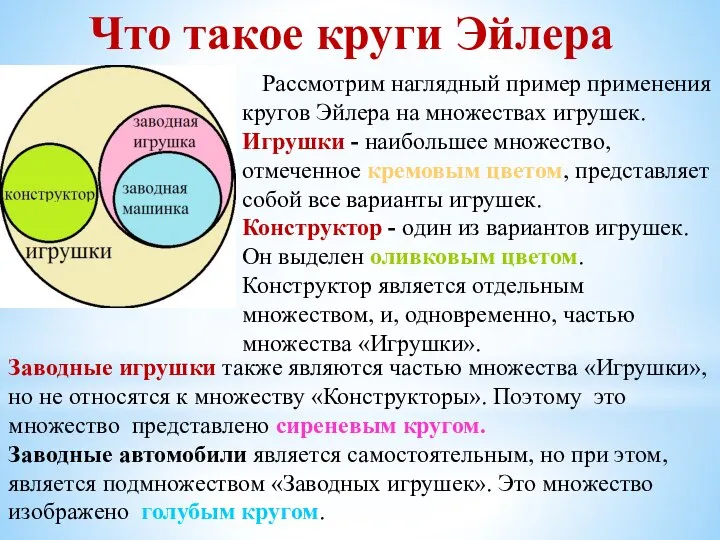
Леонард Эйлер, один из величайших математиков петербургской академии, написал около 850 научных работ. В одной из этих работ появились круги Эйлера. Впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда: «Круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный приём применил учёный Джон Венн.


 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа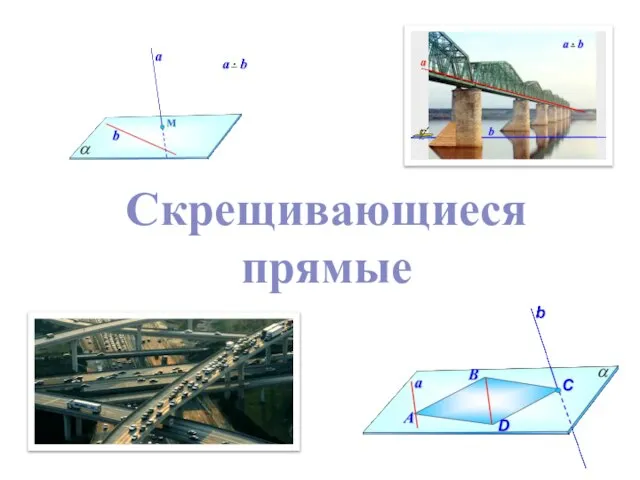 Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15