Содержание
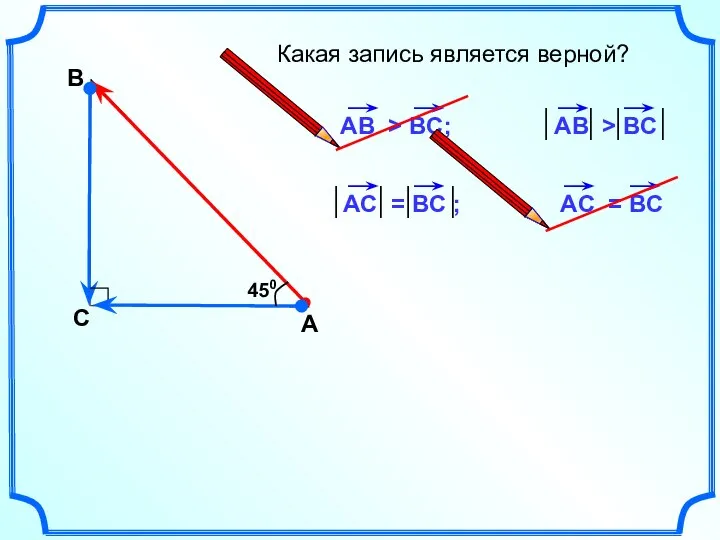
- 2. А В С Какая запись является верной? 450
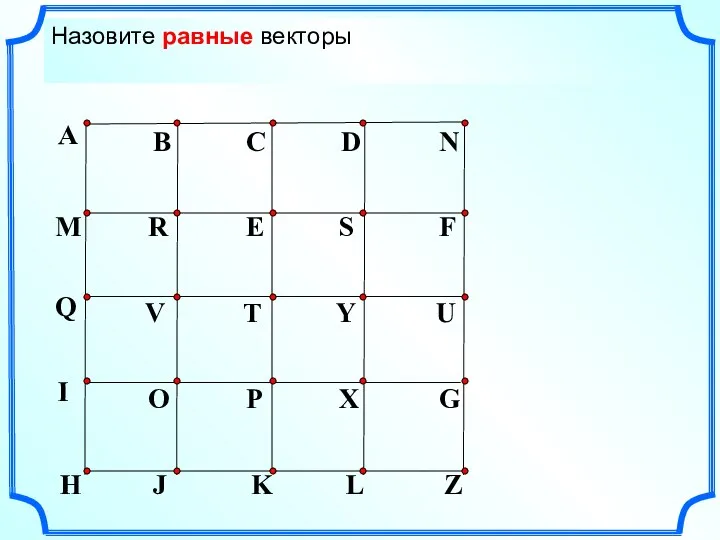
- 3. Назовите коллинеарные сонаправленные векторы Назовите коллинеарные противоположнонаправленные векторы Назовите равные векторы
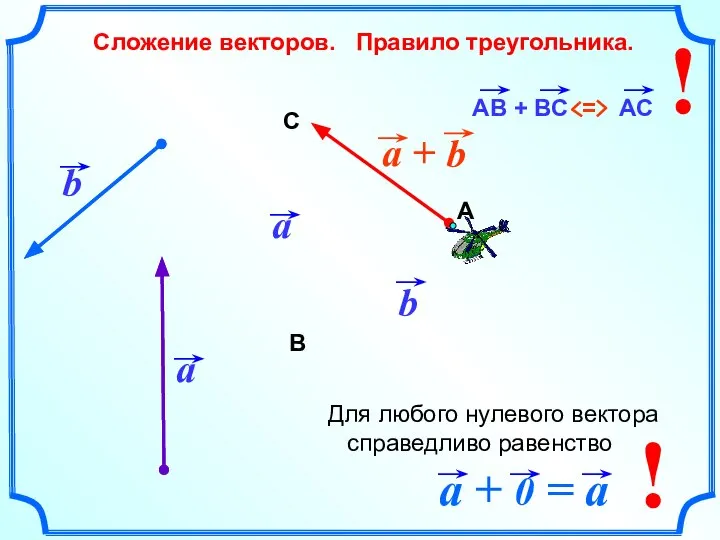
- 4. Сложение векторов. Правило треугольника. b А В С ! ! Для любого нулевого вектора справедливо равенство
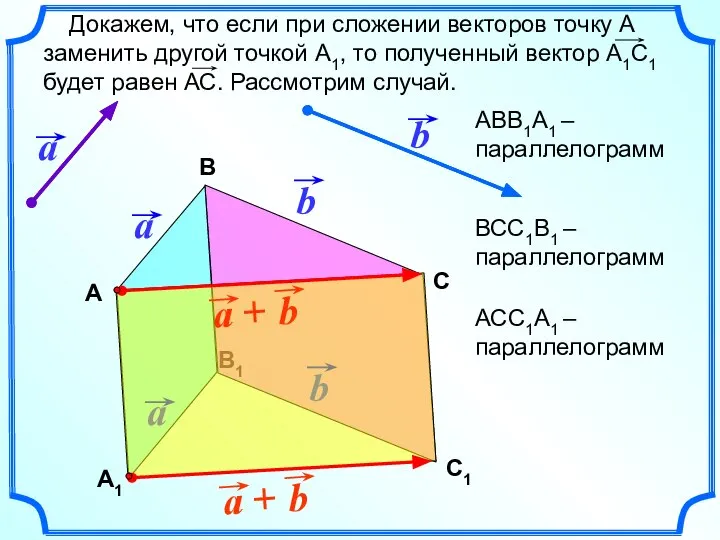
- 5. В1 Докажем, что если при сложении векторов точку А заменить другой точкой А1, то полученный вектор
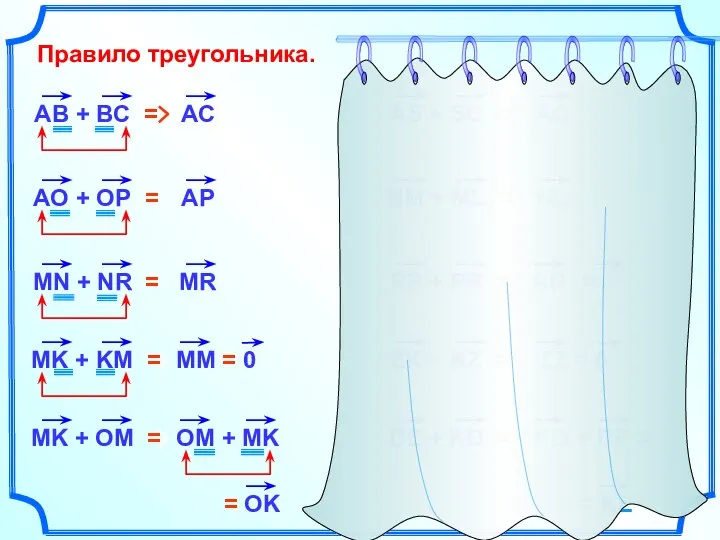
- 6. Правило треугольника. RR = 0
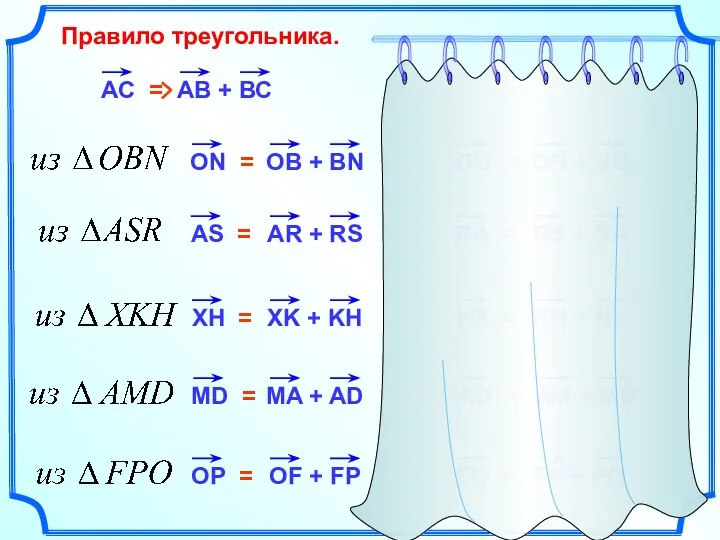
- 7. Правило треугольника. АС = OB = RA = KX = AD = FO =
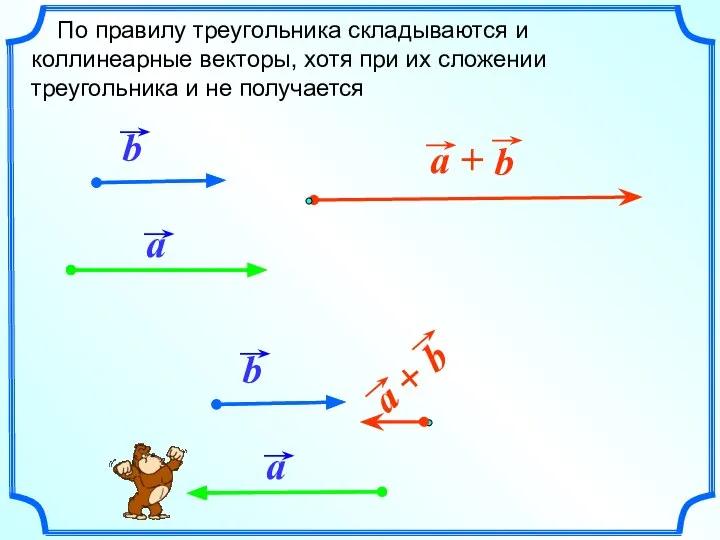
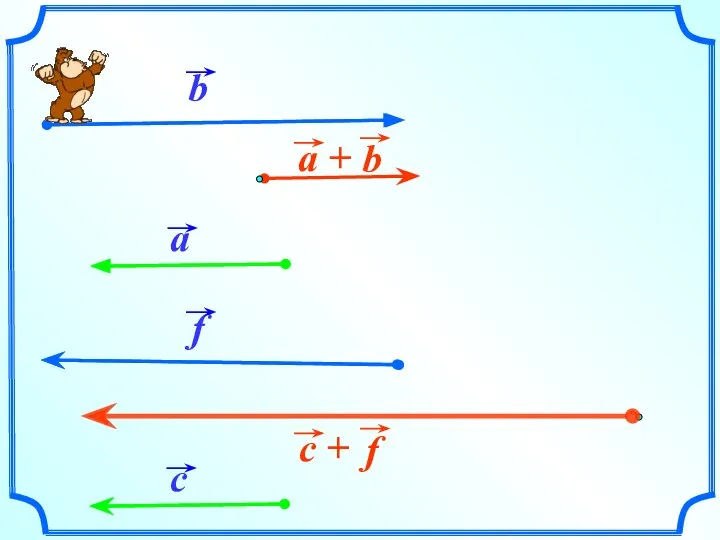
- 8. По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается
- 10. Законы сложения векторов Для любых векторов справедливы равенства: 1 2 ! ! Теорема
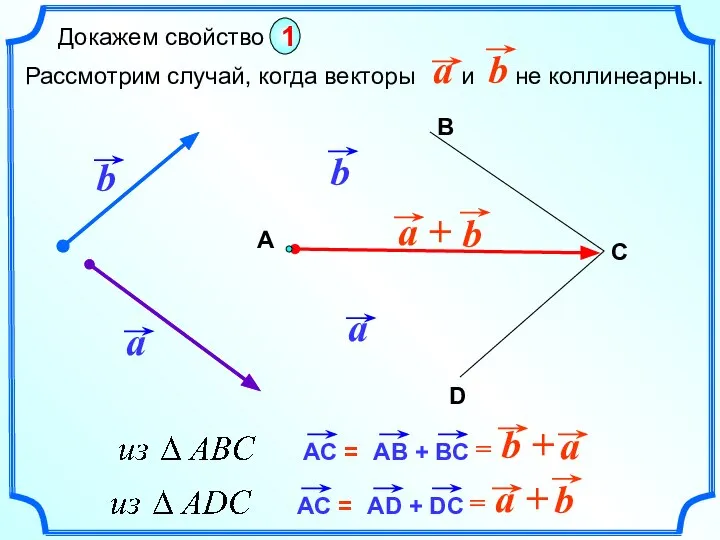
- 11. А В D C
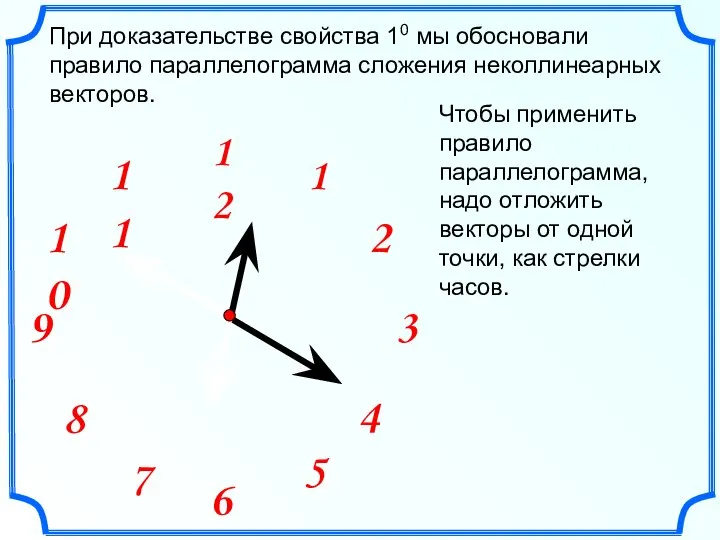
- 12. При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных векторов. Чтобы применить правило параллелограмма, надо
- 13. Сложение векторов. Правило параллелограмма.
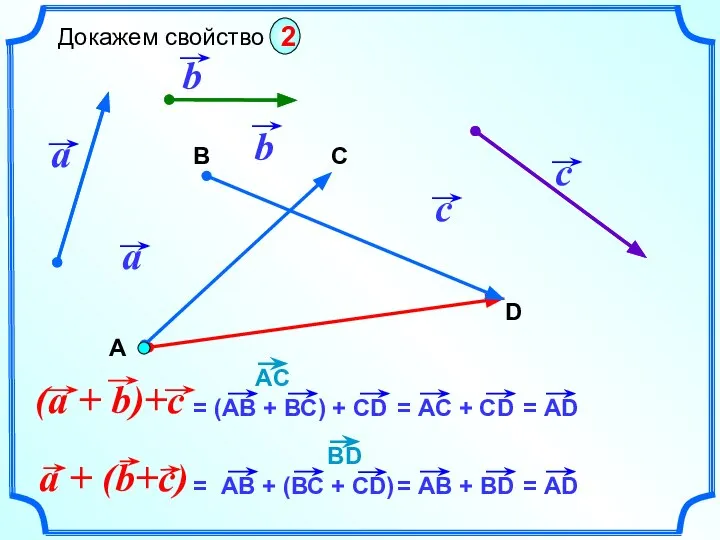
- 14. В D C Докажем свойство 2 А
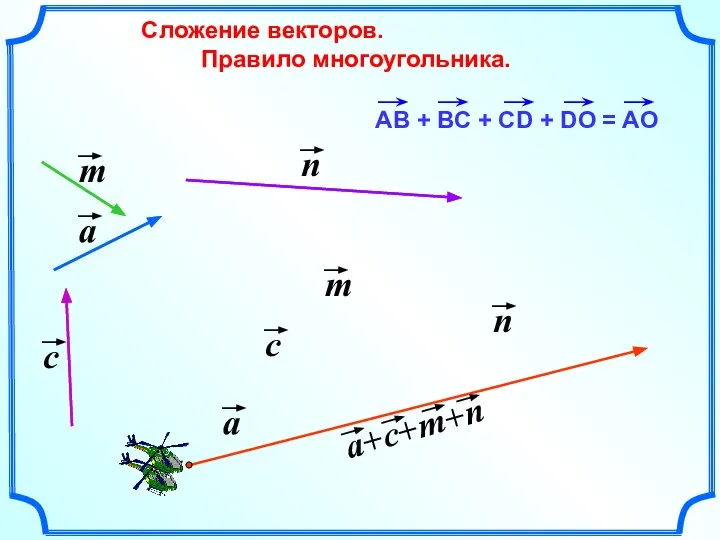
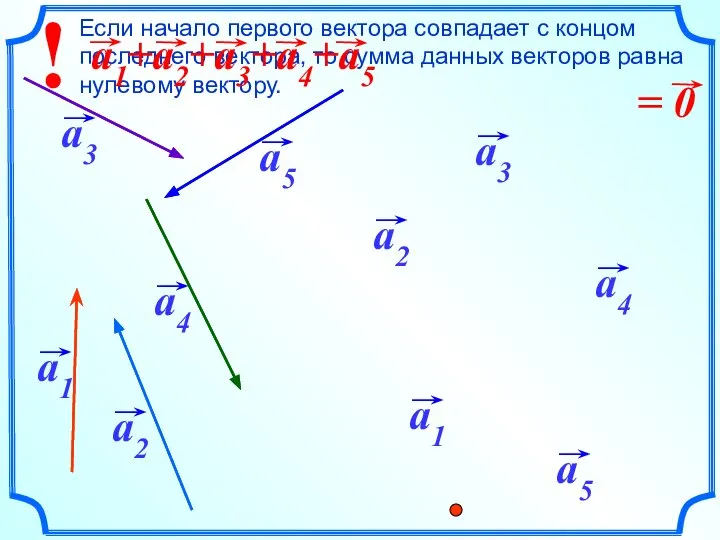
- 15. Сложение векторов. Правило многоугольника.
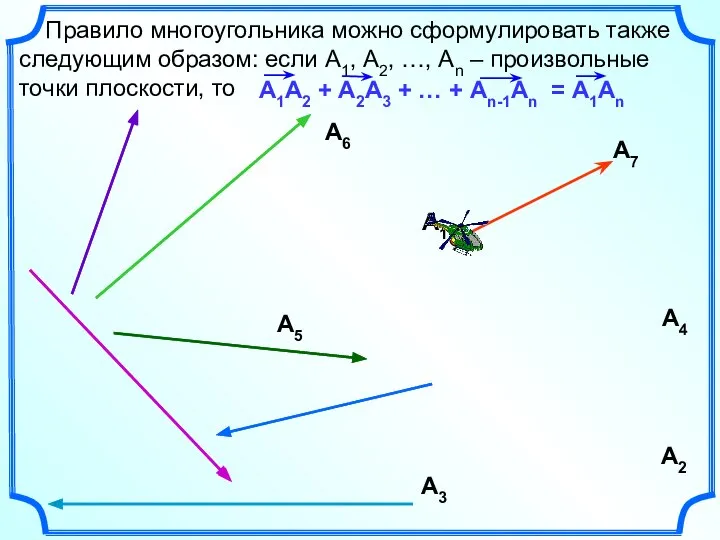
- 16. Правило многоугольника можно сформулировать также следующим образом: если А1, А2, …, Аn – произвольные точки плоскости,
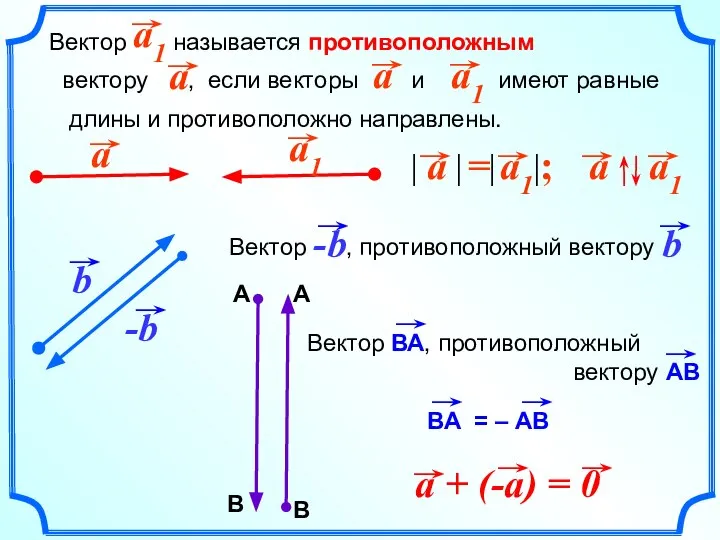
- 18. Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены.
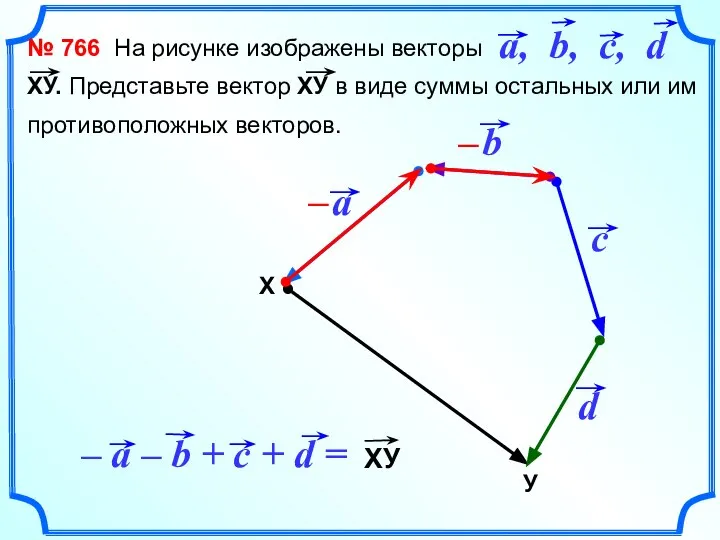
- 19. № 766 На рисунке изображены векторы ХУ. Представьте вектор ХУ в виде суммы остальных или им
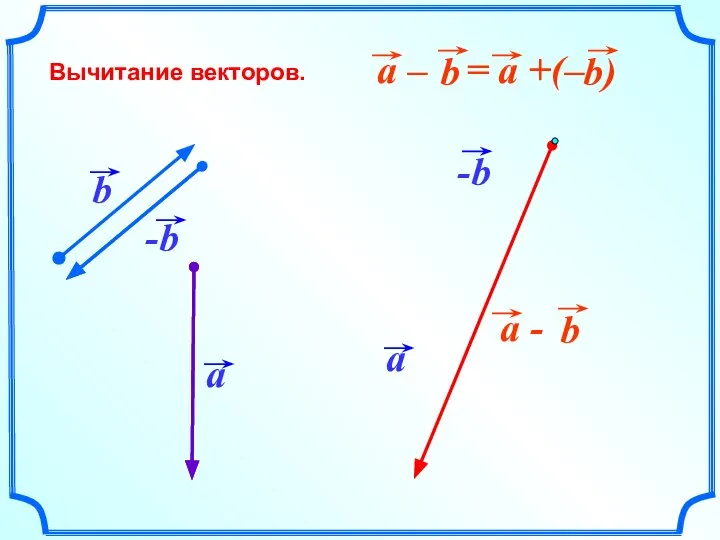
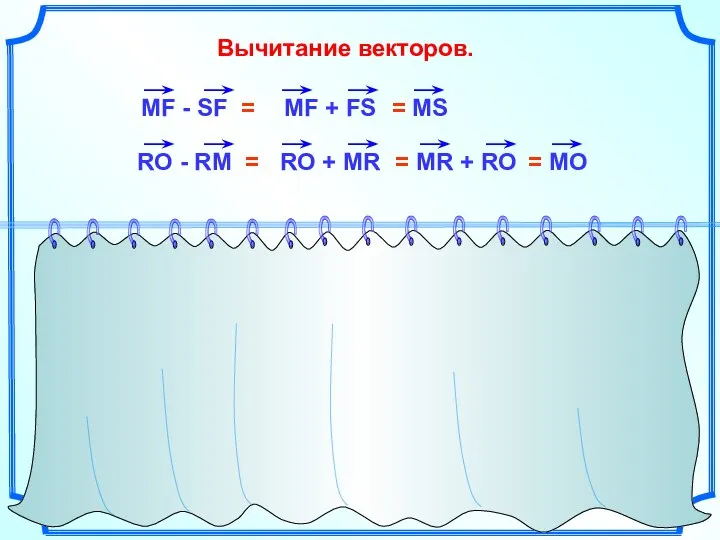
- 20. Вычитание векторов.
- 21. Вычитание векторов.
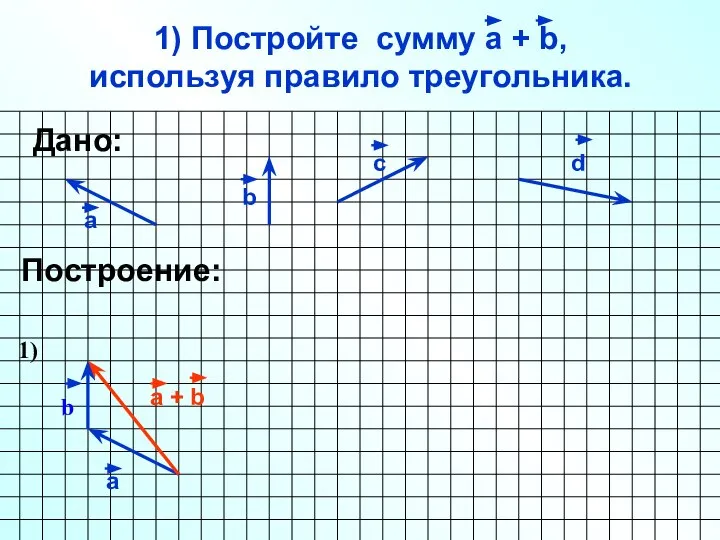
- 22. 1) Постройте сумму а + b, используя правило треугольника. а b c Построение: d Дано: а
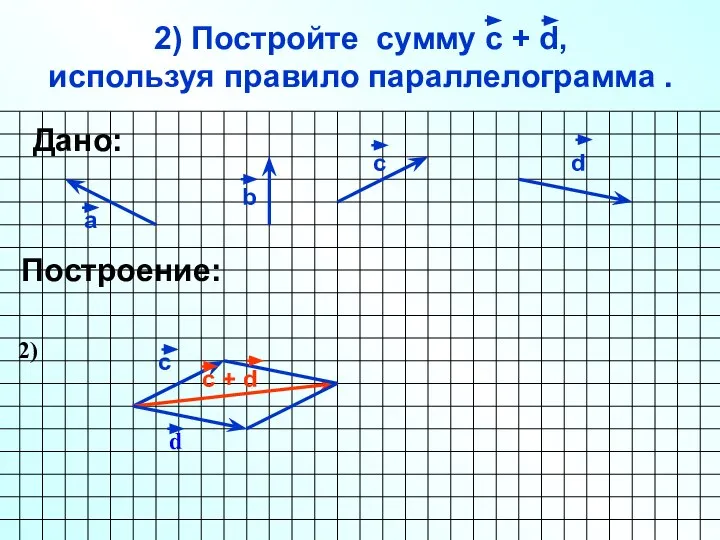
- 23. 2) Постройте сумму с + d, используя правило параллелограмма . а b c Построение: d Дано:
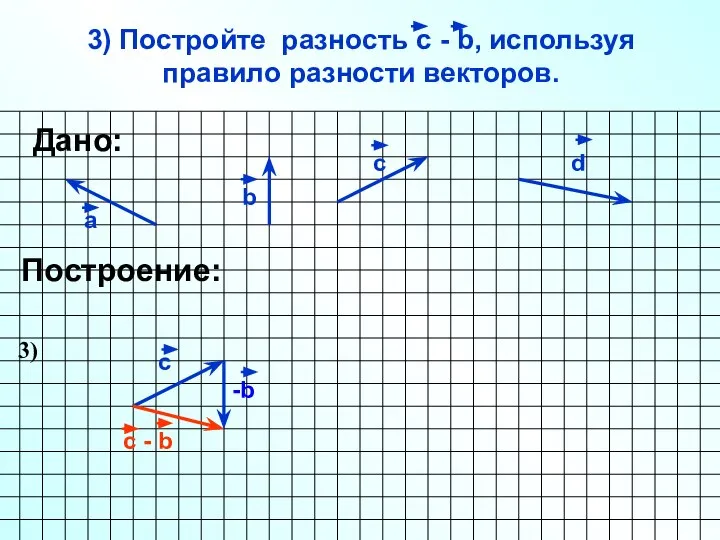
- 24. 3) Постройте разность с - b, используя правило разности векторов. а b c Построение: d Дано:
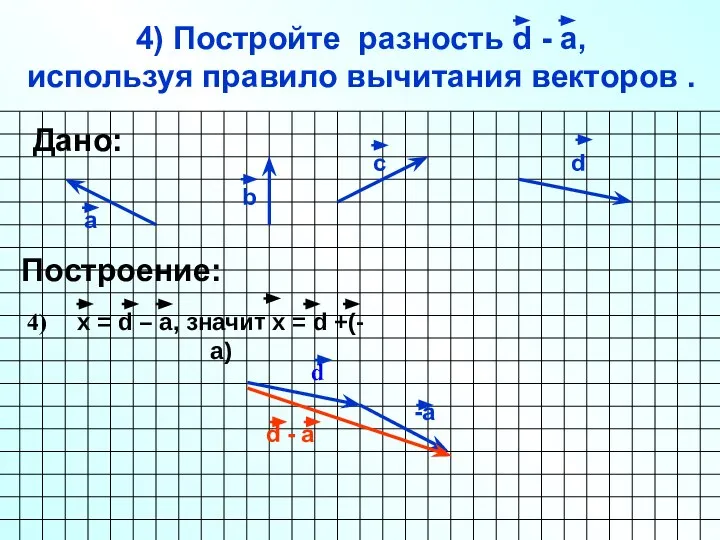
- 25. 4) Постройте разность d - а, используя правило вычитания векторов . а b c Построение: d
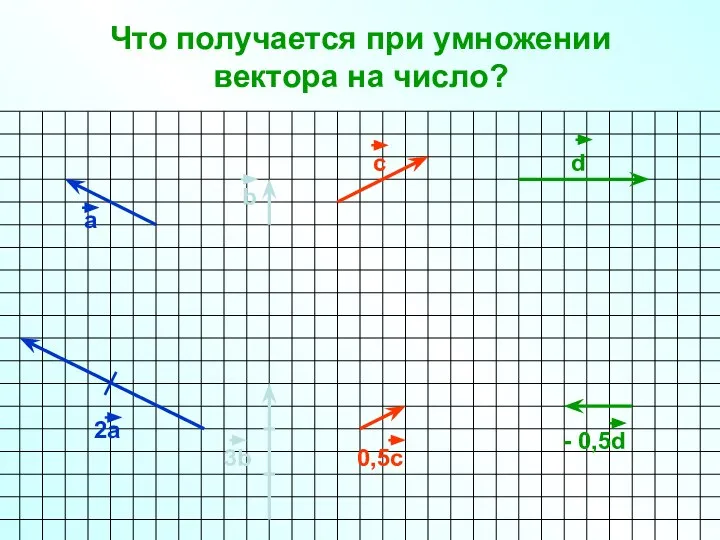
- 26. Что получается при умножении вектора на число? а b c d 2а 3b 0,5с - 0,5d
- 27. 5) Упростите выражение: 1 вариант. CA – OB – CD + AB = 2 вариант. BA
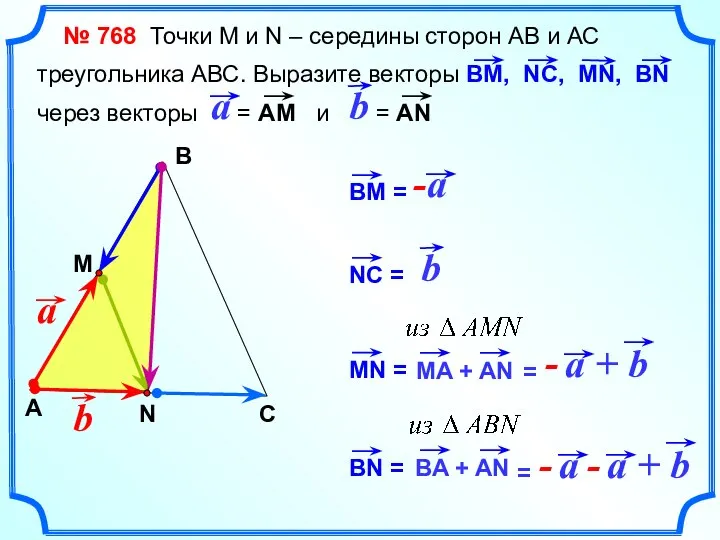
- 29. № 768 Точки М и N – середины сторон АВ и АС треугольника АВС. Выразите векторы
- 31. Скачать презентацию




 Задачи на расстояние
Задачи на расстояние Присчитывание и отсчитывание по 2
Присчитывание и отсчитывание по 2 Первое появление понятия многогранников
Первое появление понятия многогранников Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82
Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82 Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4) Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Выполни тест в электронном дневнике. Устный счёт
Выполни тест в электронном дневнике. Устный счёт Графы. Пути с таблицами
Графы. Пути с таблицами Метрологические основы анализа
Метрологические основы анализа Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Тригонометрия в биологии и медицине
Тригонометрия в биологии и медицине Тригонометрический круг
Тригонометрический круг Пифагоровы тройки чисел
Пифагоровы тройки чисел Презентация на тему Деление двузначного числа на однозначное
Презентация на тему Деление двузначного числа на однозначное  Степень с целым показателем. Блиц-опрос
Степень с целым показателем. Блиц-опрос Диаграммы
Диаграммы Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Повторение изученного материала, 1 класс
Повторение изученного материала, 1 класс Многонранники в нашей жизни
Многонранники в нашей жизни Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Многоугольники в нашей жизни
Многоугольники в нашей жизни Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Направления и лучи
Направления и лучи Современная финансовая математика
Современная финансовая математика Метод комплексных амплитуд при моделировании радиосистем. Лекция 12
Метод комплексных амплитуд при моделировании радиосистем. Лекция 12 Оригами. Проект по математике
Оригами. Проект по математике Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью