Содержание
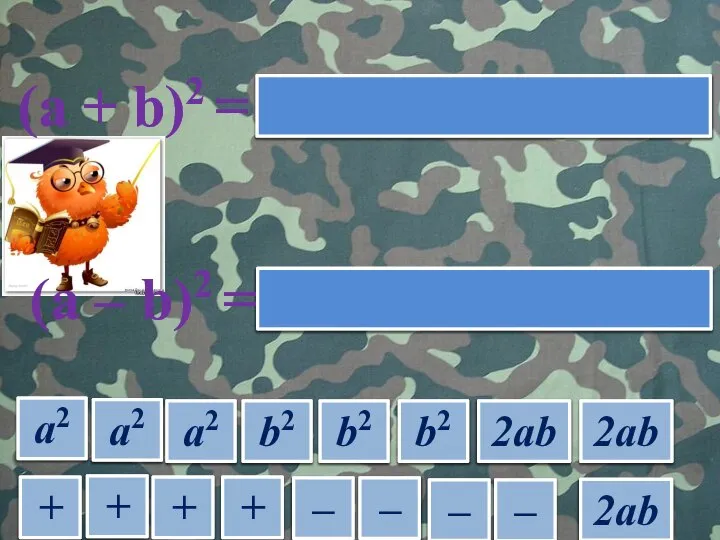
- 2. а2 + + + + – – – – а2 а2 b2 b2 b2 2ab 2ab
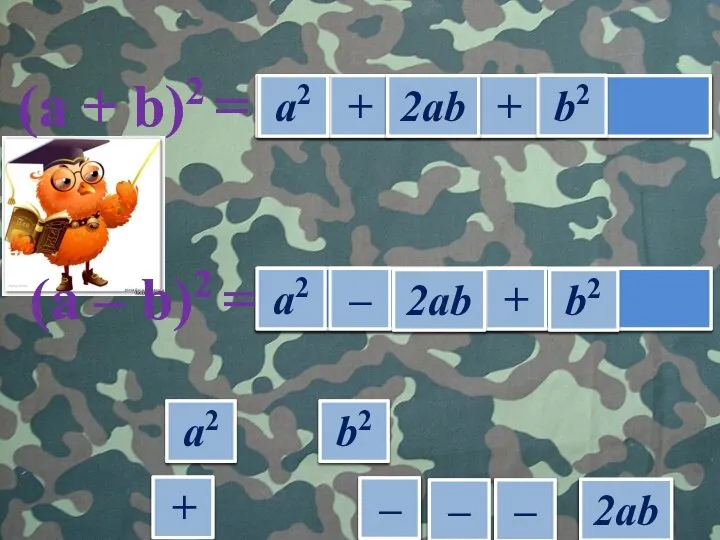
- 3. + + + + – – – – а2 а2 b2 b2 b2 2ab 2ab 2ab
- 4. (a + b)2 (– a + b)2 = (b – a)2 (a – b)2 = (b
- 5. (– a – b)2 = (a + b)2 (– a + b)2 = (b – a)2
- 6. Устная работа.
- 7. Устная работа.
- 8. Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности: (a
- 9. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе
- 10. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе
- 11. Упражнения
- 12. Упражнения
- 13. Упражнения
- 14. Упражнения
- 15. Упражнения
- 16. Упражнения
- 17. Упражнения
- 18. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 19. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 20. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 21. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 22. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 23. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 24. Упражнения Замените звёздочку одночленом так, чтобы полученный трёхчлен можно было представить в виде квадрата двучлена:
- 25. a3 + 3a2b +3ab2 + b3 a2 + 2ab + b2 a2 – 2ab + b2
- 26. a3 + 3a2b +3ab2 + b3 a2 + 2ab + b2 a2 – 2ab + b2
- 27. Задание на самоподготовку №1
- 28. Задание на самоподготовку №2
- 29. Задачи на движение: Разведывательному кораблю (разведчику), двигавшемуся в составе эскадрильи, дано задание обследовать район моря на
- 31. Скачать презентацию
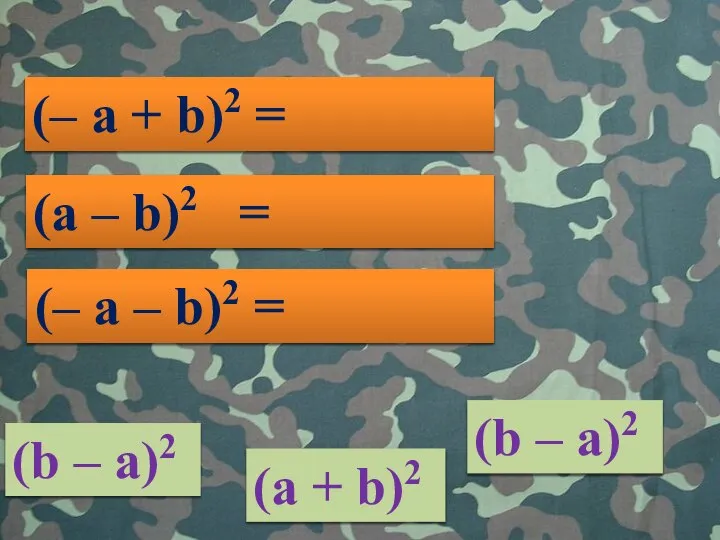
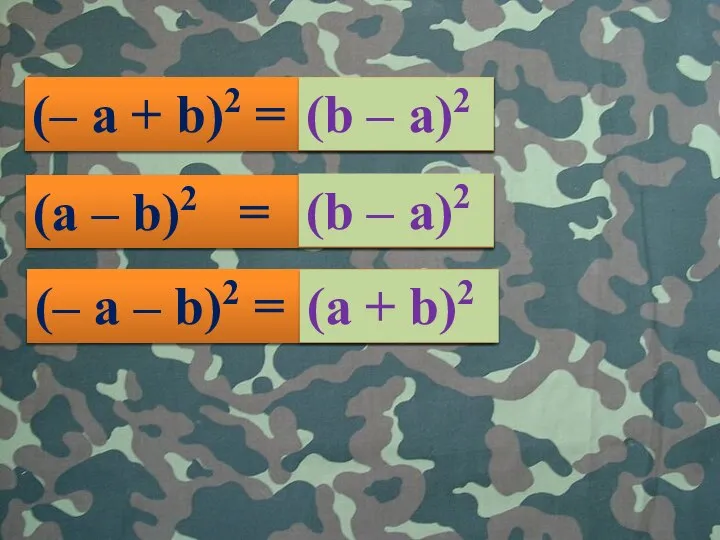























 Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс
Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс Задача №1. Лабораторная работа №5
Задача №1. Лабораторная работа №5 Решение задач по теме Треугольники. 7 класс
Решение задач по теме Треугольники. 7 класс El gran robo
El gran robo Состав числа 8
Состав числа 8 Сравнение отрезков и углов
Сравнение отрезков и углов Компетентностноориентированные задачи по алгебре для 7 класса
Компетентностноориентированные задачи по алгебре для 7 класса Эконометрика, как наука
Эконометрика, как наука Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Признаки равенства треугольников
Признаки равенства треугольников Линии и углы в окружности
Линии и углы в окружности Радианная Мера Угла
Радианная Мера Угла Презентация на тему Километр (3 класс)
Презентация на тему Километр (3 класс)  Графики функций. Задания
Графики функций. Задания Площадь треугольника
Площадь треугольника Умножение на 1. Проведите динозаврика по лабиринту (2)
Умножение на 1. Проведите динозаврика по лабиринту (2) Геометрия вокруг нас
Геометрия вокруг нас 1 урок Векторы
1 урок Векторы Методика исследования понятия числа и его разрядной структуры, счетных операций
Методика исследования понятия числа и его разрядной структуры, счетных операций Десятичные дроби и мы
Десятичные дроби и мы Виды и особенности нелинейных систем
Виды и особенности нелинейных систем Подготовка к диагностической работе
Подготовка к диагностической работе Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Массивы. Работа с массивами
Массивы. Работа с массивами Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Функциональная грамотность на уроках математики начальных классов
Функциональная грамотность на уроках математики начальных классов Центральные и вписанные углы. Решение задач
Центральные и вписанные углы. Решение задач Школьный портфель. Буква Ы. Счёт до 7
Школьный портфель. Буква Ы. Счёт до 7