Слайд 2Цели:
формировать умения решать квадратные неравенства; развивать логическое мышление, умение работать в

проблемной ситуации;
активизировать познавательную и творческую деятельность.
Слайд 3Задание 1
При каких значениях а неравенство ах²+2ах+2х+2а+2≤0
выполняется при любых значениях х?

Слайд 4Решение:
а)неравенство выполняется при любых значениях х, если
ах²+х∙(2а+2)+2а+2≤0
D =(2а)²-4а ∙(2а+2)=4а

²+8а+4-8а²-8а=4-4а=4∙(1-а²)=4∙(1-а)∙(1+а)
Итак, при а ≤-1, уравнение имеет корни при любых значениях х
Ответ: при а ≤-1
Слайд 5Задание 2
а)При каких значениях а решением неравенства (х-а)²(х-3)(х+1) ≤0
является сплошной промежуток?
б)

При каких значениях а неравенство
выполняется при всех значениях х из отрезка
Слайд 6Решение а):
а)рассмотрим «плавающую» точку а на отрезке прямой относительно точек -1 и

3
1) а<3 не удв.услов.
2) а=3 удв.услов.
3) -1<а<3 удв.услов.
4) а= -1 удв.услов.
5) а< -1 не удв.услов.
Ответ: при -1≤а≤3
Слайд 7Решение б):
1) при а >0
<а<1
2)при а<0 нет решений
Ответ: при

Слайд 8Задание 3
Найти все а, при которых неравенство
имеет не менее трех целых решений.

Слайд 9Решение:
Рассмотрим две функции
и выполним рисунок:
При а=4 нер-во примет вид при х=±2
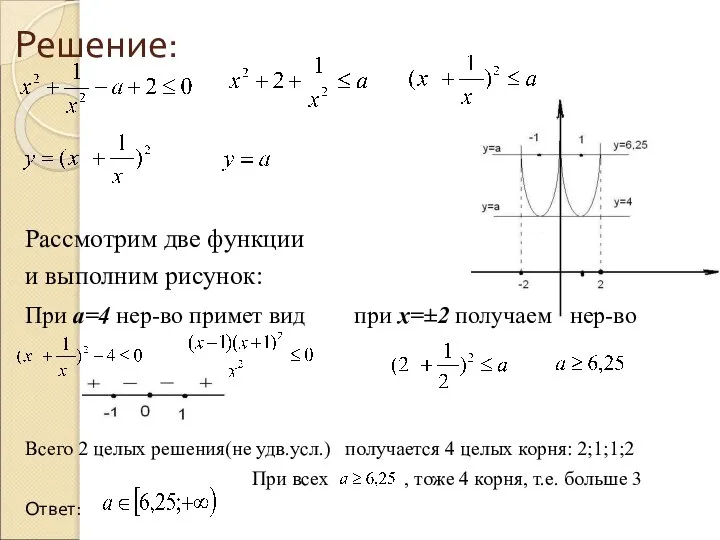
получаем нер-во
Всего 2 целых решения(не удв.усл.) получается 4 целых корня: 2;1;1;2
При всех , тоже 4 корня, т.е. больше 3
Ответ:
Слайд 10Задание 4
Найти все а, при которых неравенство
имеет ровно два целых решения.

Слайд 11Решение:
Рассмотрим две функции и выполним рисунок:
При 0≤а<1,8 нер-во имеет ровно 2 целых
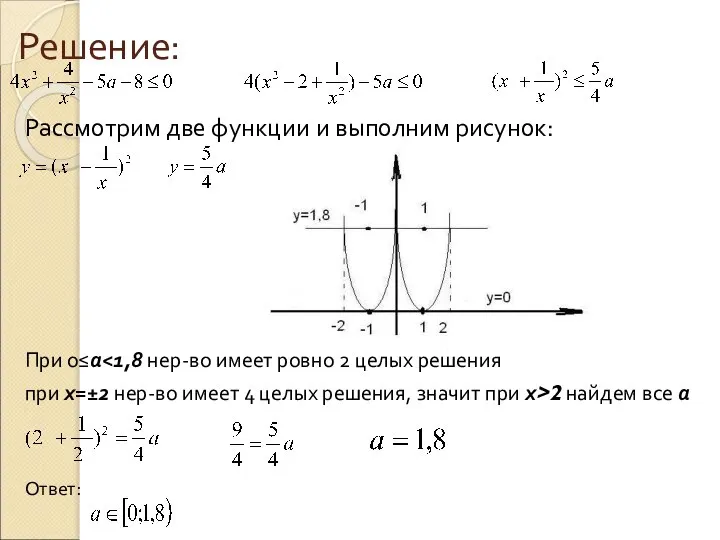
решения
при х=±2 нер-во имеет 4 целых решения, значит при х>2 найдем все а
Ответ:










 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник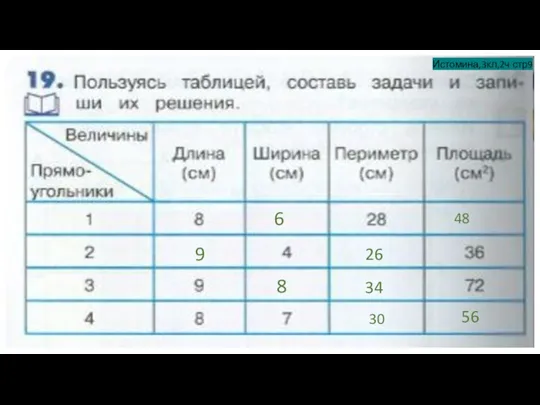 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика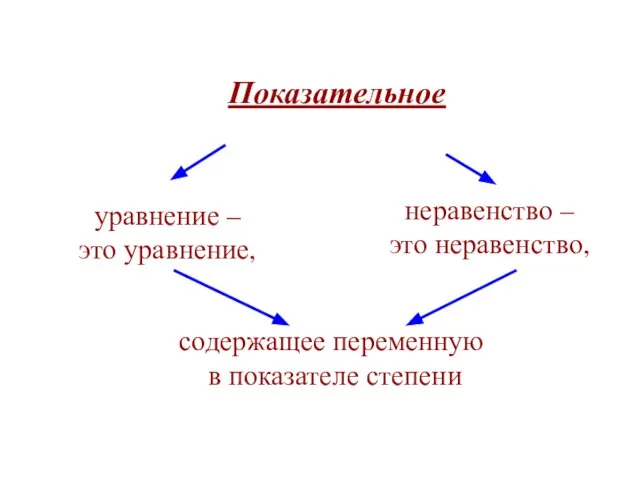 Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность