Содержание
- 2. Матрицы. Основные понятия Матрицей называется прямоугольная таблица, составленная из каких – либо элементов и имеющая m
- 3. Матрицы. Основные понятия
- 4. Матрицы. Основные понятия Квадратная матрица называется единичной, если ее элементы, расположенные на главной диагонали, равны единице,
- 5. Матрицы. Основные понятия Для каждой квадратной матрицы n - ного порядка существует определитель n - ного
- 6. Действия над матрицами Равенство матриц Матрицы равны, если они имеют одинаковую размерность и их соответствующие элементы
- 7. Действия над матрицами Сложение (вычитание) матриц Сумма и разность матриц существуют только для матриц одинакового размера,
- 8. Действия над матрицами Умножение матрицы на число Найти значение выражения: При умножении матрицы A на число
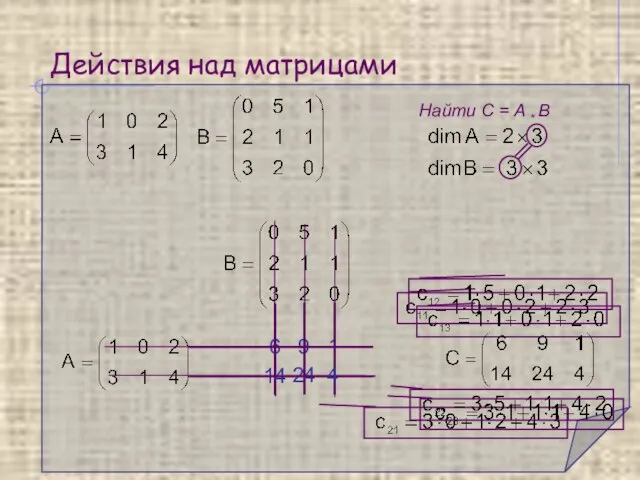
- 9. Действия над матрицами Умножение матриц Произведение матриц A * B определено только тогда, когда число столбцов
- 10. Действия над матрицами Найти С = A * B 6 9 1 14 24 4
- 11. Действия над матрицами Свойства операции произведения матриц: 1) 2) 3) 4) В общем случае для произведения
- 12. Действия над матрицами Нахождение обратной матрицы Обратная матрица обозначается символом А-1. Таким образом, согласно определению: АА-1=А-1А=Е.
- 14. Скачать презентацию










 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов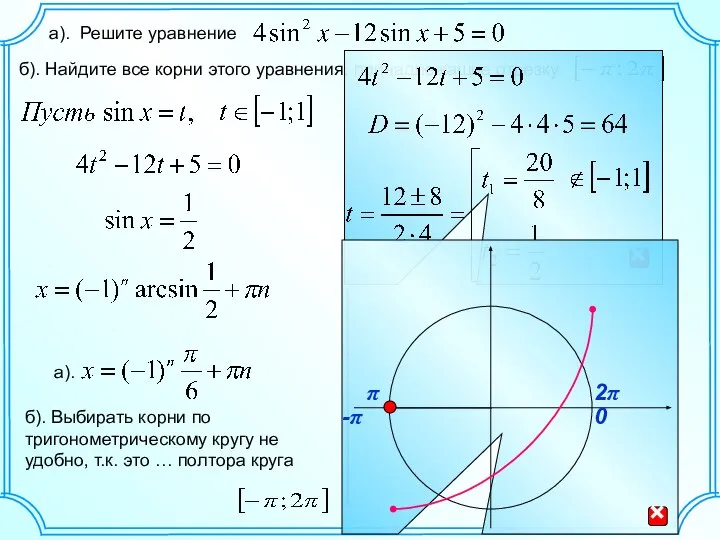 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители