Логарифмическая функция

Цели урока:
Образовательные - познакомить учащихся с логарифмической функцией, её основными свойствами, графиком; показать использование свойств, потребность к самообразованию, способствовать развитию творческой деятельности учлогарифмической функции при решении заданий.
Развивающие – развивать математическую речь учащихсяащихся.
Воспитательные - воспитывать познавательную активность, чувства ответственности, взаимоподдержки, уверенности в себе; воспитывать культуру общения.

В области математики Джон Непер известен как изобретатель системы логарифмов, основанной на установлении соответствия между арифметической и геометрической числовыми прогрессиями. В «Описании удивительной таблицы логарифмов» он опубликовал первую таблицу логарифмов (ему же принадлежит и сам термин «логарифм»), но не указал, каким способом она вычислена. Объяснение было дано в другом его сочинении «Построение удивительной таблицы логарифмов», вышедшем в 1619, уже после смерти Непера. Таблицы логарифмов, насущно необходимые астрономам, нашли немедленное применение.
Джон Непер

Функцию, заданную формулой
y = loga x (где а > 0 и а ≠ 1),
называют логарифмической функцией с основанием а
Определение логарифмической функции

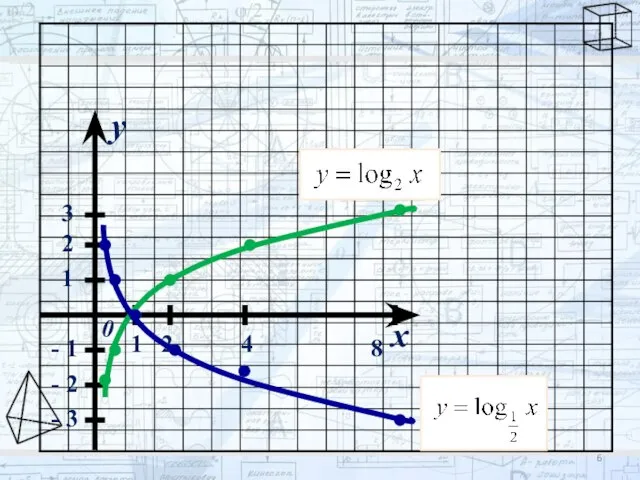
Построить графики функций
y = log2x и y = log1/2x

x
y
0
1
2
3
1
2
4
8
- 1
- 2
- 3

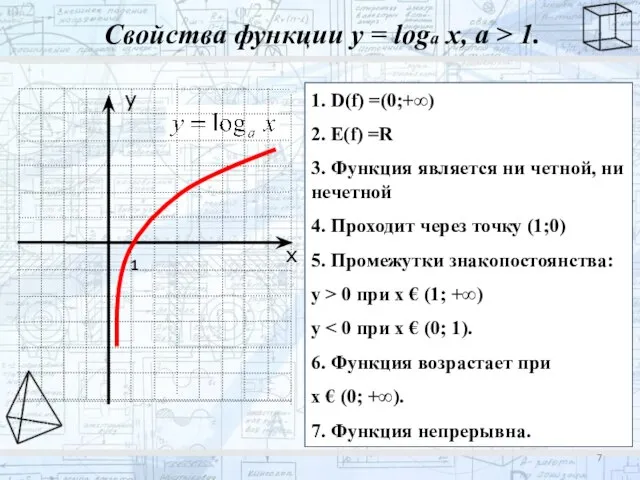
Свойства функции у = loga x, a > 1.
1. D(f) =(0;+∞)
2. E(f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у > 0 при x € (1; +∞)
у < 0 при х € (0; 1).
6. Функция возрастает при
x € (0; +∞).
7. Функция непрерывна.

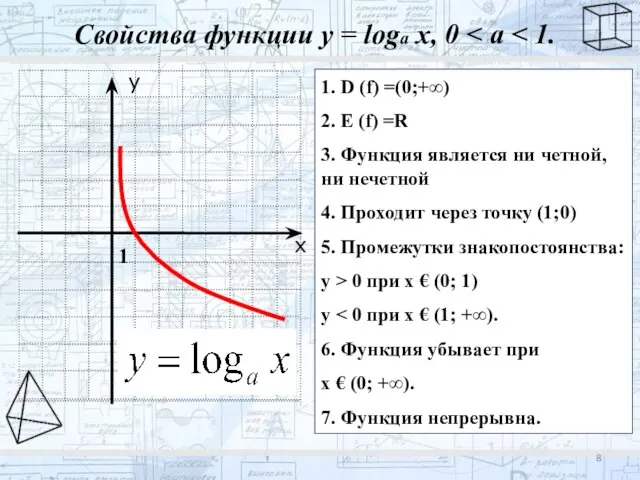
Свойства функции у = loga x, 0 < a < 1.
1. D (f) =(0;+∞)
2. E (f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у > 0 при x € (0; 1)
у < 0 при х € (1; +∞).
6. Функция убывает при
x € (0; +∞).
7. Функция непрерывна.

Леонард Эйлер
Идеальный математик 18 века - так часто называют Эйлера. Он родился в маленькой тихой Швейцарии. В 1725 году переехал в Россию. Поначалу Эйлер расшифровывал дипломатические депеши, обучал молодых моряков высшей математике и астрономии, составлял таблицы для артиллерийской стрельбы и таблицы движения Луны. В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. Там "король математиков" работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Современное определение показательной, логарифмической и тригонометрических функций – заслуга Эйлера, так же как и их символика.

Определите, какие из перечисленных ниже функций являются возрастающими, а какие убывающими:
1) y = log3 x;
2) y = log2 x;
3) y = log0,2 x;
4) y = log0,5 (2x+5);
5) y = log3 (x+2)

Используя свойства
логарифмической функции, сравнить:
а) lоg2 3 и log2 5;
б) log2 1/3 и log2 1/5;
в)log1/2 3 и log1/2 5;
г)log1/2 1/3 и log1/2 1/5.