Содержание
- 2. Криволинейной трапецией называется фигура, ограниченная отрезками прямых х = а, х = b, y = 0
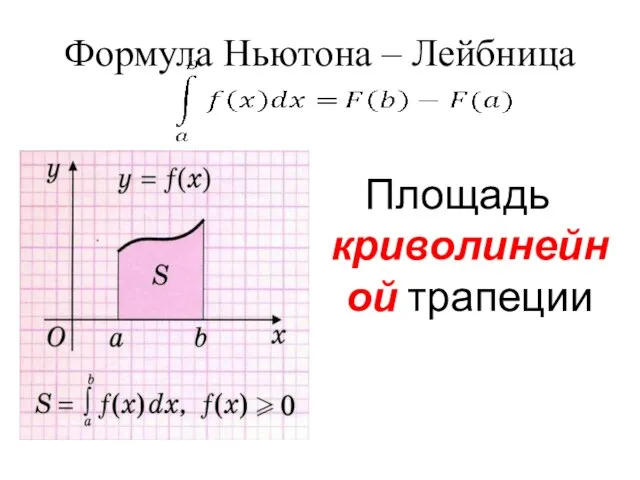
- 3. Формула Ньютона – Лейбница Площадь криволинейной трапеции
- 4. Вычислить площадь криволинейной трапеции
- 5. Площадь фигуры равна сумме площадей криволинейных трапеций
- 6. Площадь фигуры равна разности площадей криволинейных трапеций
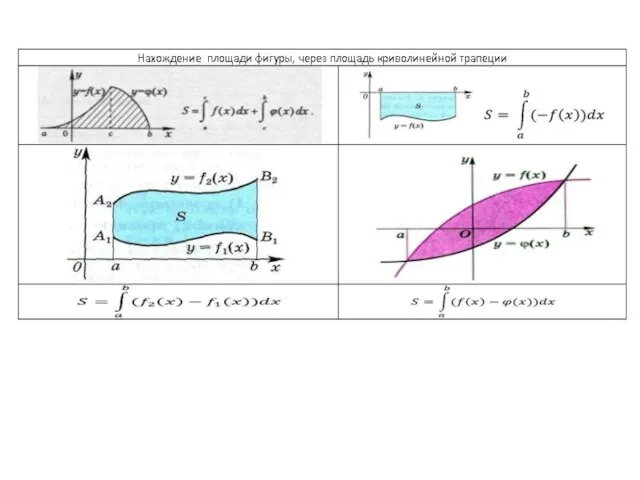
- 7. Площадь фигуры вычисляется как разность площадей криволинейных трапеций на отрезке [a;b] Если функции у = f(x)
- 8. Искомая площадь фигуры равна площади фигуры, симметричной данной относительно оси Ох Если f(x) 0 на отрезке
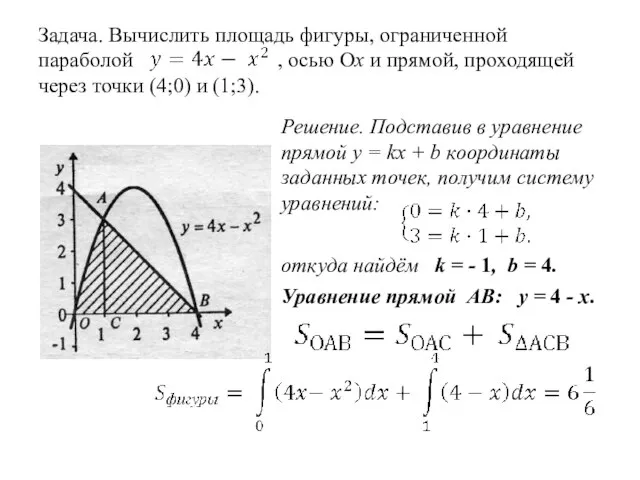
- 10. Задача. Вычислить площадь фигуры, ограниченной параболой , осью Ох и прямой, проходящей через точки (4;0) и
- 11. Задача. Вычислить площадь фигуры, ограниченной параболой , осью Ох и прямой, проходящей через точки (4;0) и
- 12. Задача. Найти площадь фигуры, ограниченной линиями Решение. Точки пересечения заданных линий: О(0;0), К(6;0), Р(4;2) Фигура состоит
- 13. Решение. Найдём абсциссы точек пересечения этих графиков из уравнения Искомая площадь равна сумме площадей криволинейных трапеций
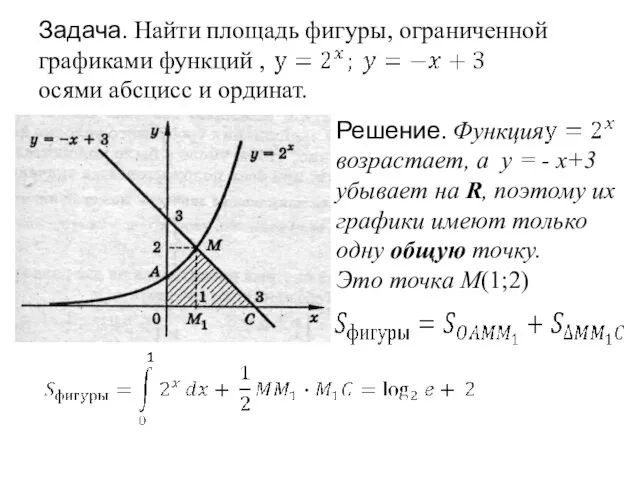
- 14. Задача. Найти площадь фигуры, ограниченной графиками функций , осями абсцисс и ординат. Решение. Функция возрастает, а
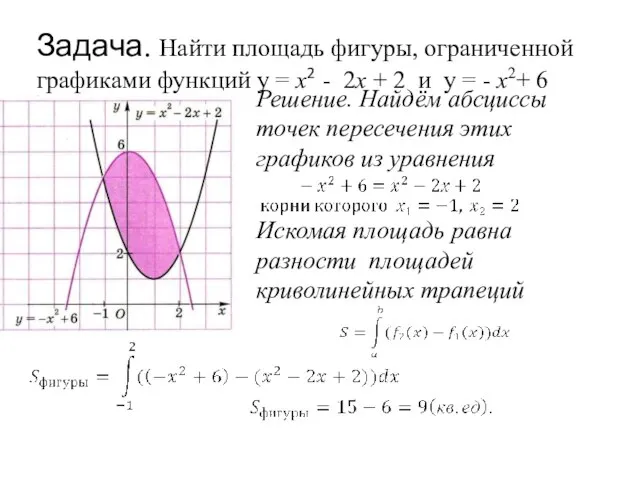
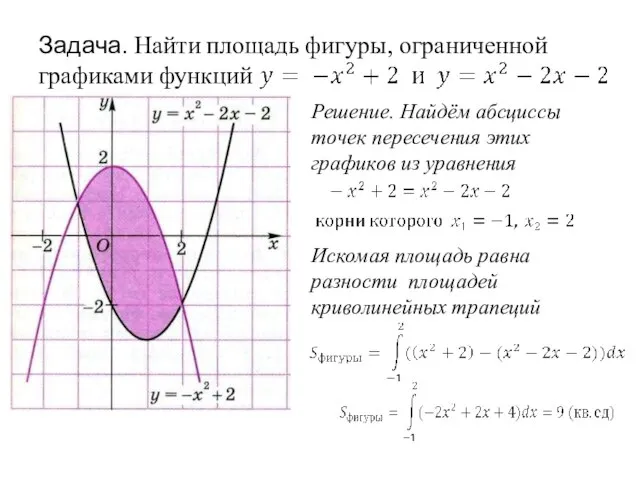
- 15. Задача. Найти площадь фигуры, ограниченной графиками функций y = x2 - 2x + 2 и y
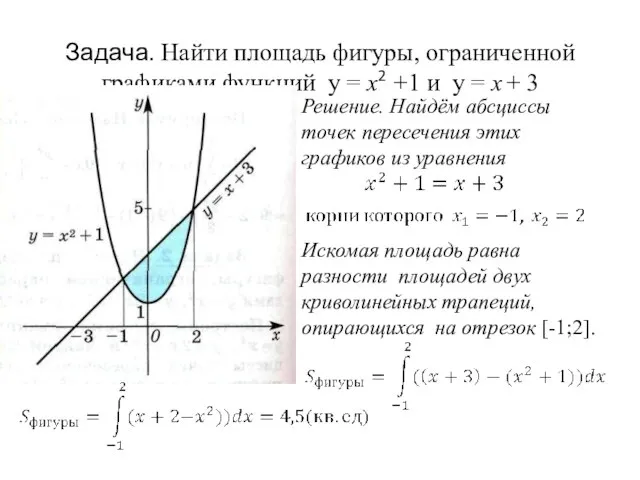
- 16. Задача. Найти площадь фигуры, ограниченной графиками функций y = x2 +1 и y = x +
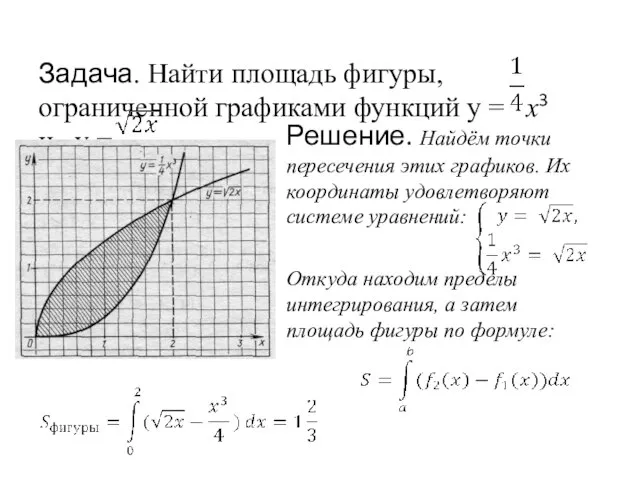
- 17. Задача. Найти площадь фигуры, ограниченной графиками функций y = x3 и y = Решение. Найдём точки
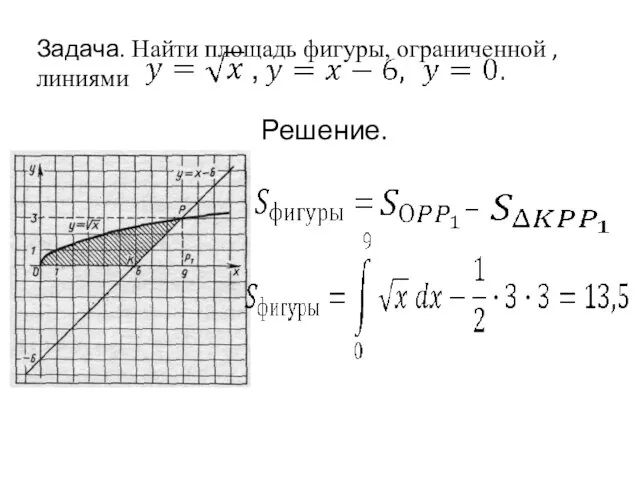
- 18. Задача. Найти площадь фигуры, ограниченной , линиями , – Решение.
- 19. Задача. Найдите площадь фигуры, ограниченной линиями Решение.
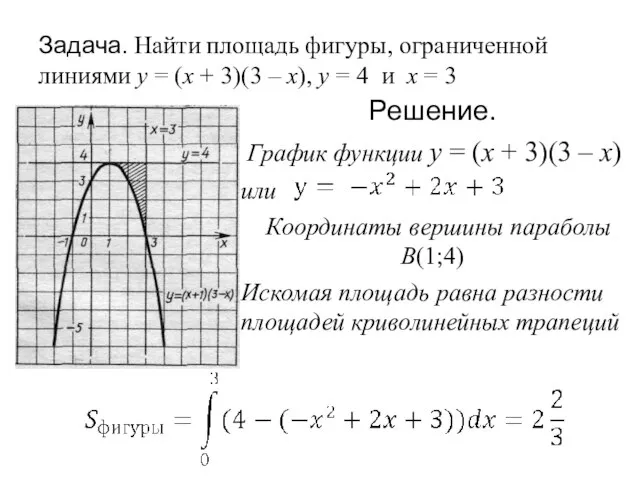
- 20. Задача. Найти площадь фигуры, ограниченной линиями y = (x + 3)(3 – x), y = 4
- 21. Задача. Найти площадь фигуры, ограниченной графиком функции и осями координат Решение. Заданная фигура представляет собой криволинейную
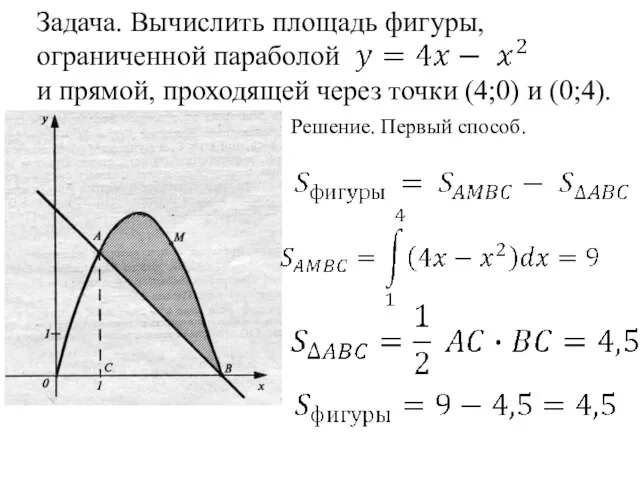
- 22. Задача. Вычислить площадь фигуры, ограниченной параболой и прямой, проходящей через точки (4;0) и (0;4). Решение. Первый
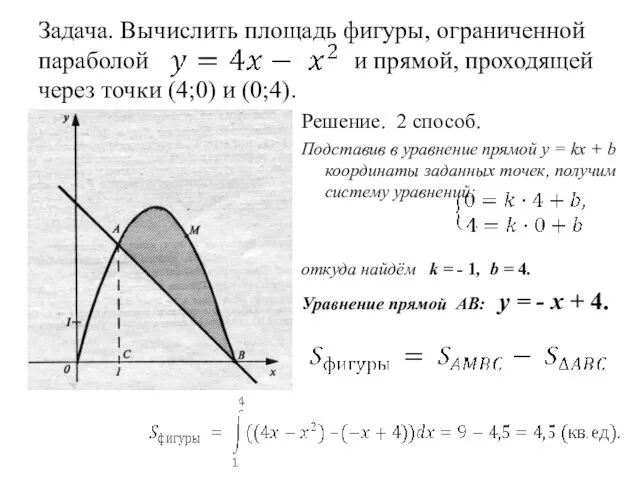
- 23. Задача. Вычислить площадь фигуры, ограниченной параболой и прямой, проходящей через точки (4;0) и (0;4). Решение. 2
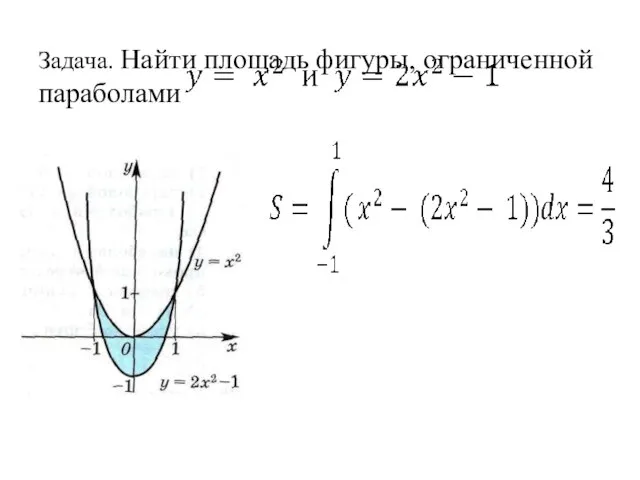
- 24. Задача. Найти площадь фигуры, ограниченной параболами
- 25. Задача. Найти площадь фигуры, ограниченной графиками функций Решение. Найдём абсциссы точек пересечения этих графиков из уравнения
- 26. По рисункам 31 – 36 назвать из каких фигур состоит фигура , площадь которой вычисляется, и
- 28. Скачать презентацию




![Площадь фигуры вычисляется как разность площадей криволинейных трапеций на отрезке [a;b] Если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/865337/slide-6.jpg)







 Деление на 3
Деление на 3 Дифференциальные уравнения 1-го порядка
Дифференциальные уравнения 1-го порядка Факторный анализ торговых алгоритмов
Факторный анализ торговых алгоритмов Математическое моделирование. Лекция 1
Математическое моделирование. Лекция 1 Төзек күпкырлыклар
Төзек күпкырлыклар Признаки параллельности прямых
Признаки параллельности прямых Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Повторение и расширение сведений о функции
Повторение и расширение сведений о функции Отношение площадей подобных треугольников
Отношение площадей подобных треугольников Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Состав числа 10
Состав числа 10 Метод параллельного переноса решения геометрических задач
Метод параллельного переноса решения геометрических задач Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Задачи. Урок 20
Задачи. Урок 20 Квадратные уравнения и неравенства
Квадратные уравнения и неравенства Показательные уравнения
Показательные уравнения Решение иррациональных уравнений
Решение иррациональных уравнений Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -  Преобразование иррациональных выражений
Преобразование иррациональных выражений КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Формулы дифференцирования
Формулы дифференцирования Математика. 2 класс
Математика. 2 класс Задача о смесях
Задача о смесях Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Цилиндр. Ось симметрии цилиндра
Цилиндр. Ось симметрии цилиндра Построение треугольника
Построение треугольника Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса