Правильные многогранники. Формула Эйлера. Правильные многогранники в философской картине мира Платона. Кубок Кеплера

На уроке:
Правильные многогранники;
Формула Эйлера;
Правильные многогранники в философской картине мира Платона;
Кубок Кеплера;
Правильные многогранники вокруг нас;
Тела Архимеда;
Звездчатые многогранники.

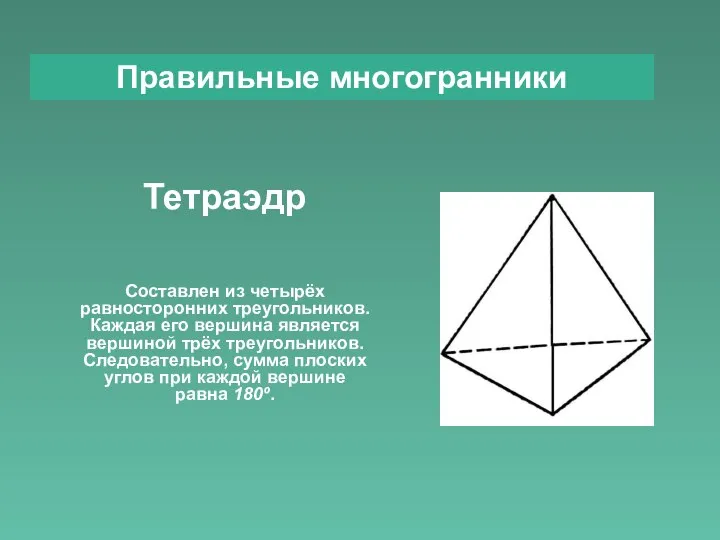
Правильные многогранники
Тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.

Правильные многогранники
Октаэдр
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240º.

Правильные многогранники
Икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º.

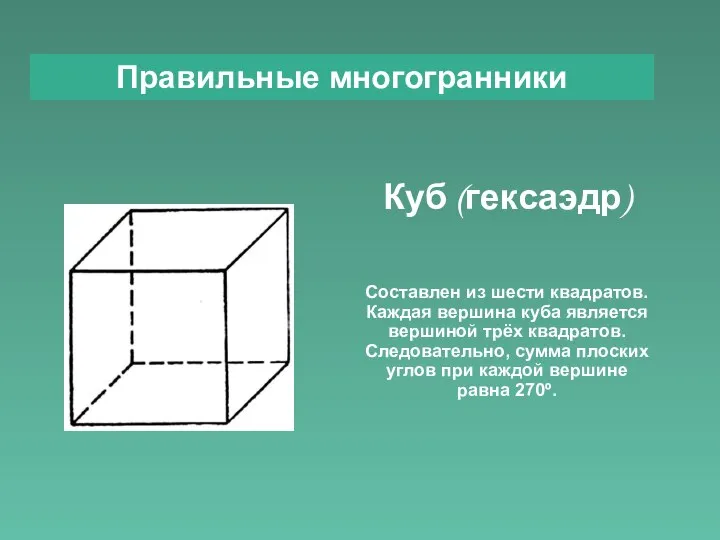
Правильные многогранники
Куб (гексаэдр)
Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º.

Правильные многогранники
Додекаэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.

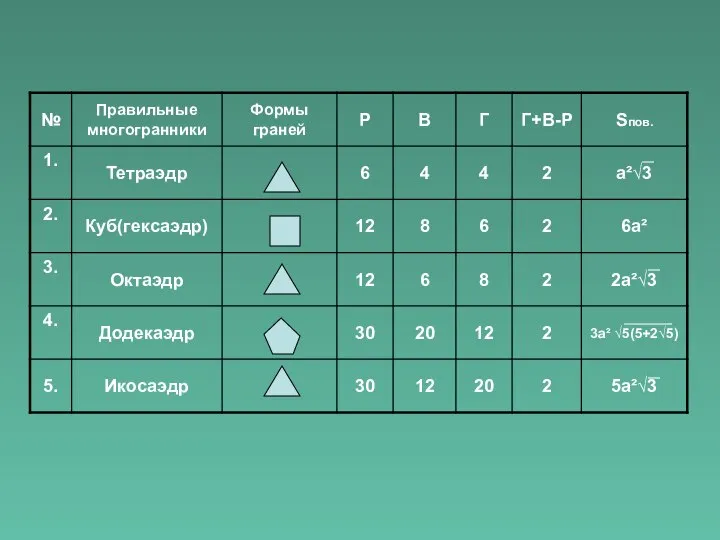
Формула Эйлера
В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.
Г + В − Р = 2

Правильные многогранники в философской картине мира Платона
Платон
(настоящее имя Аристокл)
427- 347 гг. до Р.Х
Платон получил всестороннее воспитание, которое соответствовало представлениям классической античности о совершенном, идеальном человеке, соединяющем в себе физическую красоту безупречного тела и внутреннее, нравственное благородство.
Вернувшись в Афины в 387 году, Платон основал философскую школу – Академию.

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Правильные многогранники в философской картине мира Платона

Немецкий астроном и математик Иоганн Кеплер (1571 – 1630) предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы.
В первом своем труде "Предвестник космографических исследований, содержащий космографическую тайну" (1596 г.) Кеплер суммировал свои попытки найти простые целочисленные соотношения между параметрами орбит планет.
Иоганн Кеплер

В сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия.
Космический «кубок» Кеплера

Сальвадор Дали
«Тайная вечеря»

Правильные многогранники
вокруг нас
Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] × 12H2O), монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба.
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.
Правильные многогранники
вокруг нас

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение .В начале 80-х гг. московские инженеры В. Макаров и В. Морозов высказали гипотезу, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли.
Правильные многогранники
вокруг нас
Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки.В узлах располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.
Икосаэдро-додекаэдровая структура Земли

Тела Архимеда
Архиме́д ( 287 до н.э.—212 до н.э.)
Архимед был замечательным механиком-практиком и теоретиком, но основным делом его жизни была математика.
Он значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений , корни которых он находил с помощью пересечения параболы и гиперболы.
Его работы относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя.

1) усеченный тетраэдр;
2) усеченный октаэдр;
3) усеченный икосаэдр;
4) усеченный куб;
5) усеченный додекаэдр;
Тела Архимеда
6) кубооктаэдр;
7) икосадодекаэдр;.
8) усеченный кубооктаэдр;
9) икосадодекаэдр;.
10) Ромбокубооктаэдр:
11) Ромбоикасодадекаэдр:
12) «Плосконосый»
додекаэдр:
13) «Плосконосый» куб.

Звездчатые многогранники
Они получаются из правильных многогранников продолжением граней или ребер аналогично тому, как правильные звездчатые многоугольники получаются продолжением сторон правильных многоугольников.
Первые два правильных звездчатых многогранника были открыты И. Кеплером (1571-1630), а два других почти 200 лет спустя построил французский математик и механик Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо .
Пуансо (Poinsot) Луи (3.1.1777, Париж, - 5.12.1859), французский математик и механик, член Парижской АН с 1813. Окончил Политехническую школу в Париже (1797), с 1809 профессор там же. Первые работы посвящены теории правильных звездчатых многогранников. В 1803 опубликовал "Элементы статики", в которых применил разработанные им геометрические методы исследования к учению о равновесии твёрдых тел и их систем.