Слайд 2Вопросы для повторения
1. Какое уравнение называют линейным?
2. Как решается линейное уравнение?
3. Какое

неравенство называют линейным?
4. Как решается линейное
неравенство?
Слайд 3Квадратные уравнения
а)Полные квадратные уравнения
ах2 +вх + с = 0

Слайд 5Д > 0 – 2 корня;
Д = 0 – 1 корень;
Д <

0 – нет решений
Слайд 7Решить уравнения
1. 3х2–5х - 2 = 0
2. 2 х2 -7х + 3=0
3.

2х2 - 7х + 6 =0
4. х2 – 4х + 3 = 0
5. х2 + 2х - 8 =0
6.(х – 3)(х - 2) = 6(х – 3)
Слайд 8а) Неполные квадратные
Если а ≠ 0; с отрицательное
если в=0, то ах2

- с =0
ах2 = с
х = ± √с/а
Слайд 9Пример
х2 – 16 =0
х2 = 16
х2 = 16
х1 =

- 4
х2 = 4
Ответ: х1 = - 4
х2 = 4
Слайд 10Решить уравнения:
1. 4х2 – 4 = 0
2. х2 – 25 =0

3. 3х2 – 27 =0
Слайд 11б) с = 0 ах2 + в х = 0
Выносим общий

множитель за скобки:
х(ах +в) = 0
х = 0 или ах + в = 0
Слайд 12Пример:
х2 – 3х =0
х( х – 3) = 0
х= 0

или х – 3 = 0
х = 3
Ответ: х1 = 0 и х 2= 3
Слайд 13Решить уравнения :
1. х2+27х = 0;
2. х2–9х = 0;
3. х2-25х =

0;
4. 2 х2–х = 0;
5. х2–8х = 0;












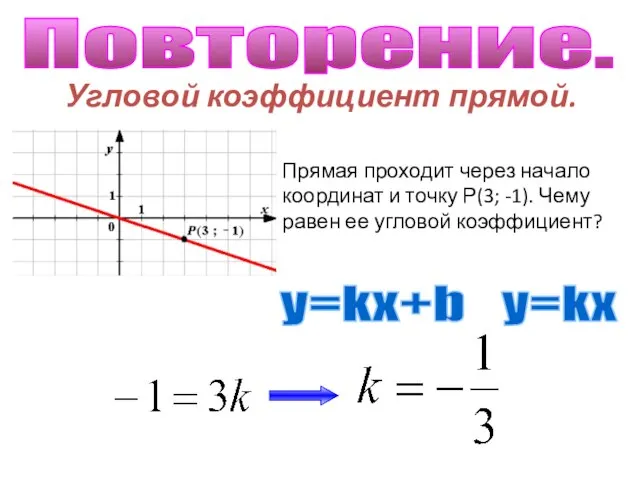 Угловой коэффициент прямой.
Угловой коэффициент прямой. Презентация на тему Десятичные дроби (6 класс)
Презентация на тему Десятичные дроби (6 класс)  Теорема Пифагора
Теорема Пифагора Градусная мера дуги окружности. Теорема о вписанном угле
Градусная мера дуги окружности. Теорема о вписанном угле Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Основы теории статистических показателей
Основы теории статистических показателей Метод ортогональных исключений. Ортогональные отражения
Метод ортогональных исключений. Ортогональные отражения Основная тенденция развития РД
Основная тенденция развития РД Центральные и вписанные углы
Центральные и вписанные углы Графики тригонометрических функций. Преобразование графиков
Графики тригонометрических функций. Преобразование графиков Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Презентация на тему Небесная геометрия
Презентация на тему Небесная геометрия  Умножение натуральных чисел
Умножение натуральных чисел Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Элементы комбинаторики АТ
Элементы комбинаторики АТ Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Баскетбол. Математическая викторина
Баскетбол. Математическая викторина Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Математическая статистика
Математическая статистика Решение текстовых задач на ЕГЭ
Решение текстовых задач на ЕГЭ Последовательность процентных расчетов при осуществлении банковских операций
Последовательность процентных расчетов при осуществлении банковских операций Один и много
Один и много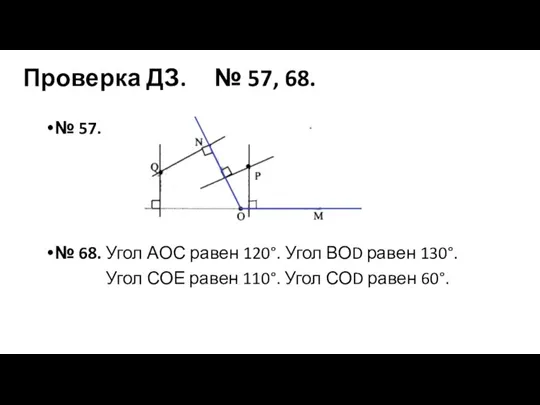 Подготовка к контрольной работе
Подготовка к контрольной работе Стереометрия. Тренажер
Стереометрия. Тренажер Параллельные плоскости
Параллельные плоскости