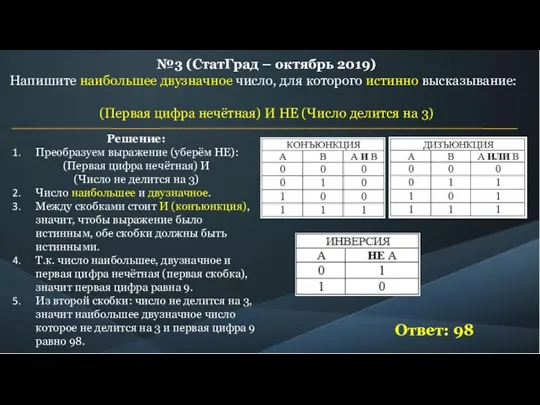
(Первая цифра нечётная) И (Число делится на 3)
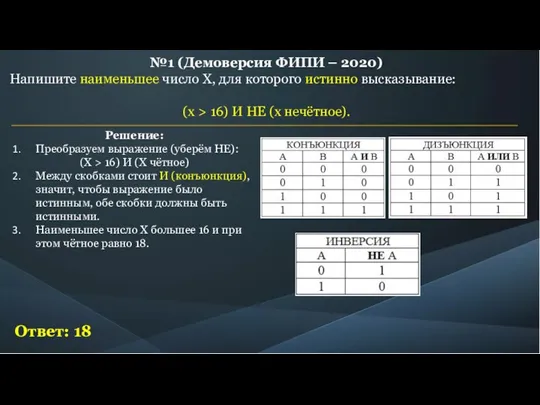
Решение:
Преобразуем выражение (уберём НЕ):
(Первая цифра чётная) И
(Число делится на 3)
Число наименьшее и двузначное.
Между скобками стоит И (конъюнкция), значит, чтобы выражение было истинным, обе скобки должны быть истинными.
Т.к. число наименьшее, двузначное и первая цифра чётная (первая скобка), значит первая цифра равна 2.
Из второй скобки: число делится на 3, значит наименьшее двузначное число которое делится на 3 и первая цифра 2 равно 21.
Ответ: 21



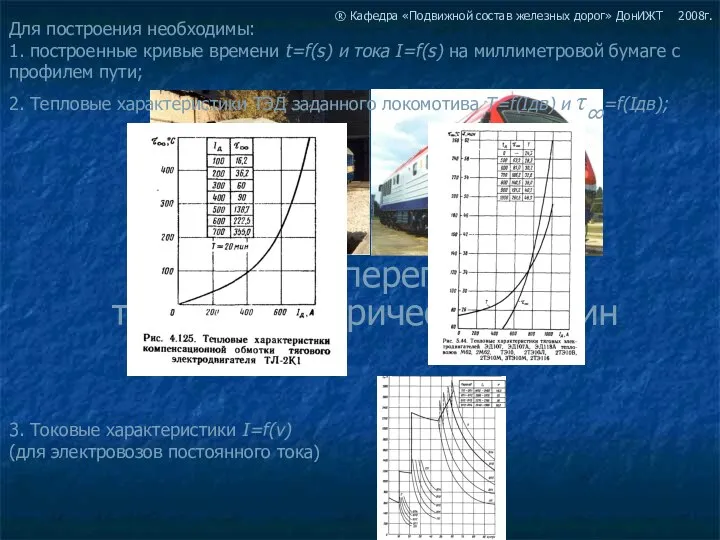 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Презентация на тему СВОЙСТВА ДВИЖЕНИЯ
Презентация на тему СВОЙСТВА ДВИЖЕНИЯ  Дискретные случайные величины
Дискретные случайные величины Свойства решений уравнения Левнера
Свойства решений уравнения Левнера Интерактивная игра. Математический футбол
Интерактивная игра. Математический футбол Задачи на движение. Встречное движение
Задачи на движение. Встречное движение повторение 7-9
повторение 7-9 Решение задач
Решение задач Признаки параллельности прямых
Признаки параллельности прямых Своя игра. Алгоритмы
Своя игра. Алгоритмы Повторение изученного в 5 классе
Повторение изученного в 5 классе Интегрированное занятие математики и истории Отечества для группы 3 года обучения
Интегрированное занятие математики и истории Отечества для группы 3 года обучения Путешествие в мир обыкновенных
Путешествие в мир обыкновенных Метрические соотношения в прямоугольном треугольнике
Метрические соотношения в прямоугольном треугольнике Геометрические построения. 7 класс
Геометрические построения. 7 класс Статистика. Занятие 5
Статистика. Занятие 5 Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) элементы теории множеств
элементы теории множеств Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Числовые и буквенные выражения
Числовые и буквенные выражения Задания по математике. 3 класс
Задания по математике. 3 класс Движение в математике
Движение в математике Математические основы информатики. Элементы комбинаторики. (Тема 1)
Математические основы информатики. Элементы комбинаторики. (Тема 1) Треугольники
Треугольники ОДУ высших порядков
ОДУ высших порядков Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Презентация на тему Распределительный закон умножения
Презентация на тему Распределительный закон умножения  Вариация управления
Вариация управления