Содержание
- 2. РАССМОТРИТЕ КАРТИНКИ И СДЕЛАЙТЕ ВЫВОД, О ЧЕМ ПОЙДЕТ РЕЧЬ НА УРОКЕ
- 3. Цели: Рассмотреть взаимное расположение двух прямых в пространстве. Ввести понятие параллельных и скрещивающихся прямых. Доказать теоремы
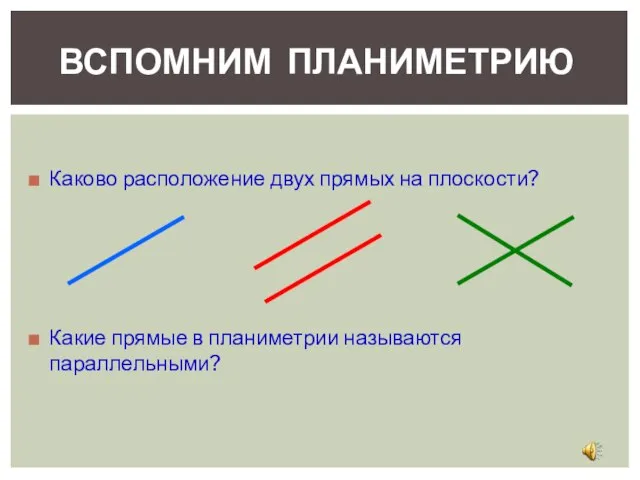
- 4. ВСПОМНИМ ПЛАНИМЕТРИЮ Каково расположение двух прямых на плоскости? Какие прямые в планиметрии называются параллельными?
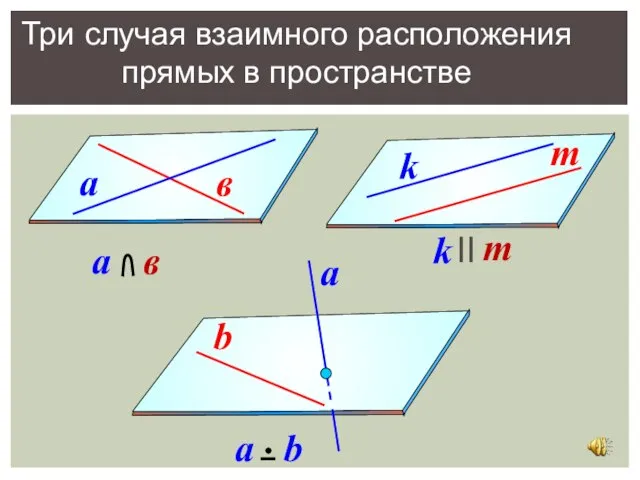
- 5. Три случая взаимного расположения прямых в пространстве
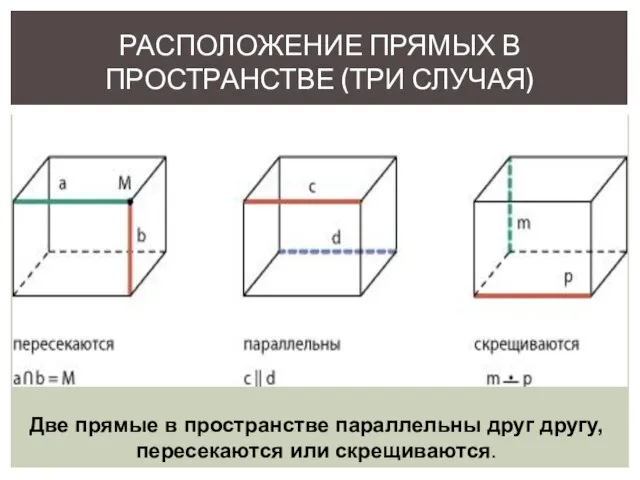
- 6. РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ (ТРИ СЛУЧАЯ) Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.
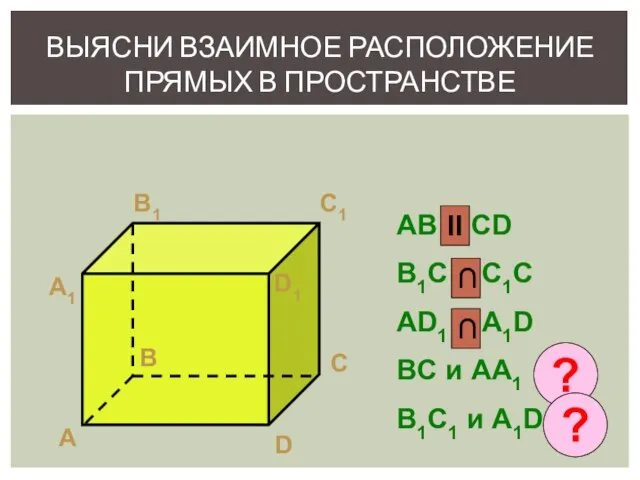
- 7. ВЫЯСНИ ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ А B C D А1 B1 C1 D1 AB и
- 8. КАКИЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ НАЗЫВАЮТСЯ ПАРАЛЛЕЛЬНЫМИ? Определение Две прямые в пространстве называются параллельными, если они лежат
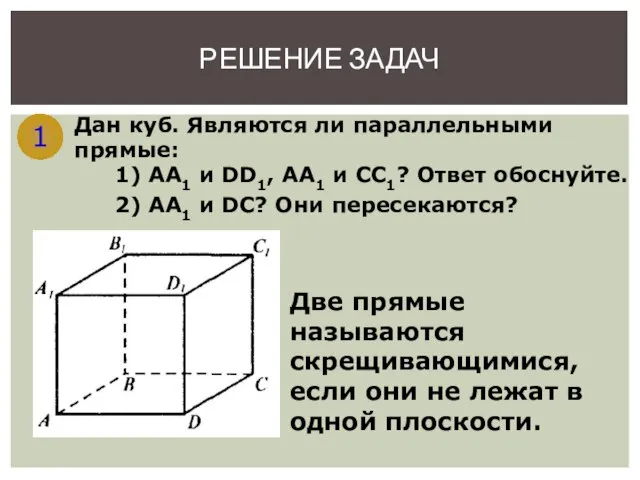
- 9. 1 Дан куб. Являются ли параллельными прямые: 1) АА1 и DD1, АА1 и СС1? Ответ обоснуйте.
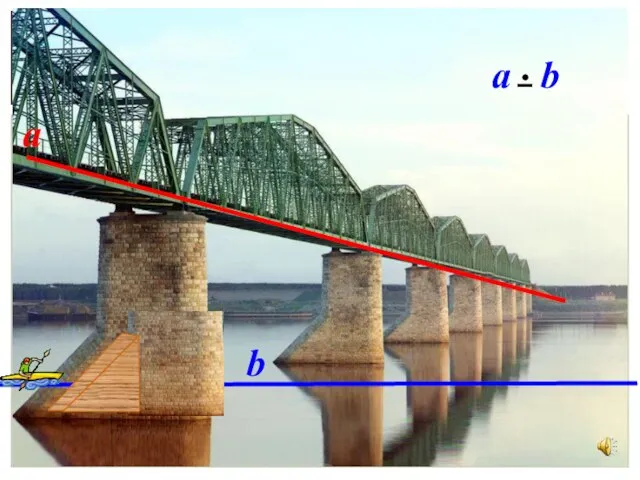
- 10. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а
- 11. a b
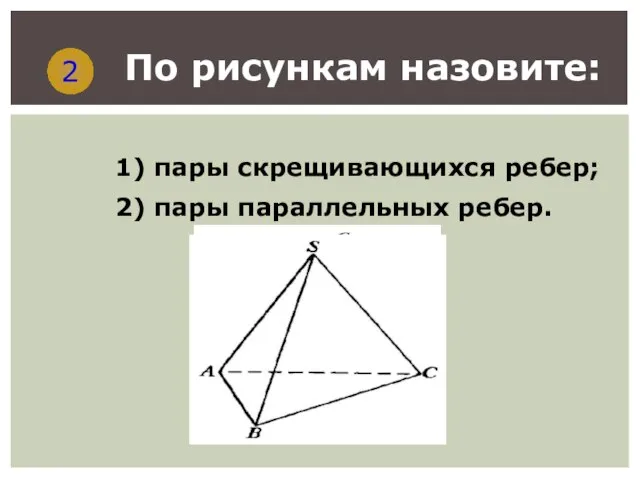
- 12. 2 По рисункам назовите: 1) пары скрещивающихся ребер; 2) пары параллельных ребер.
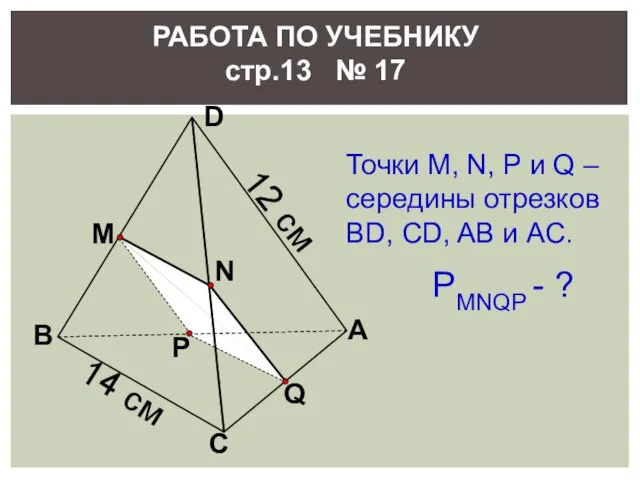
- 13. Q А С В D N M P РАБОТА ПО УЧЕБНИКУ стр.13 № 17 РMNQP -
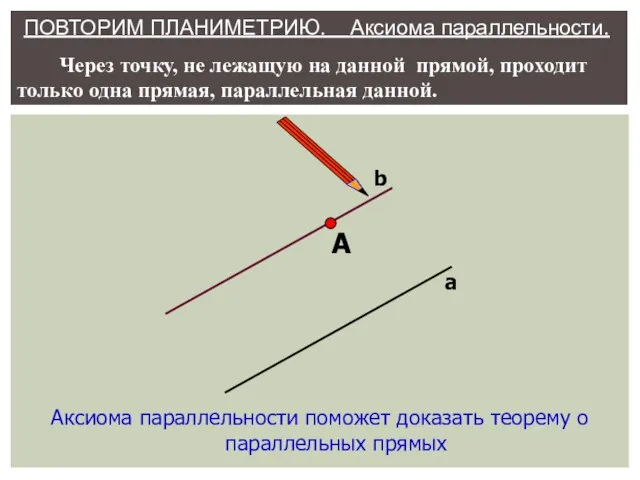
- 14. А Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. ПОВТОРИМ ПЛАНИМЕТРИЮ.
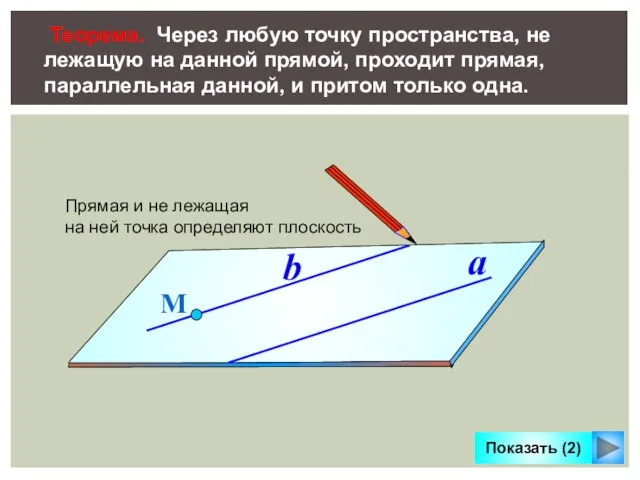
- 15. Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом
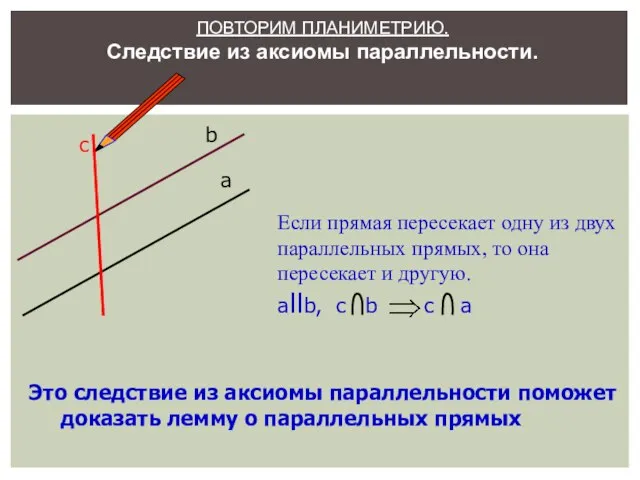
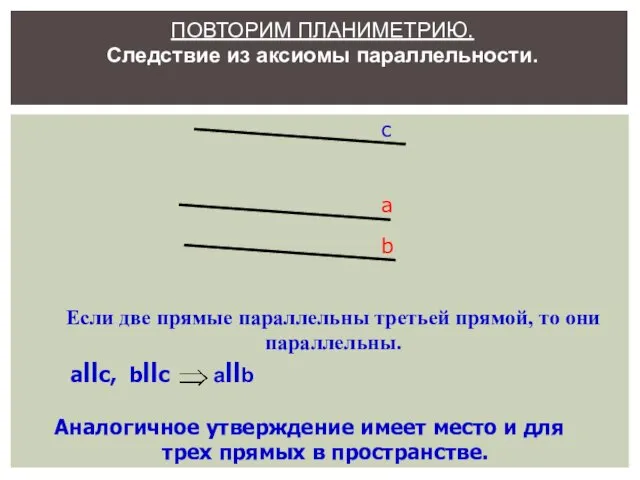
- 16. ПОВТОРИМ ПЛАНИМЕТРИЮ. Следствие из аксиомы параллельности. а c b Это следствие из аксиомы параллельности поможет доказать
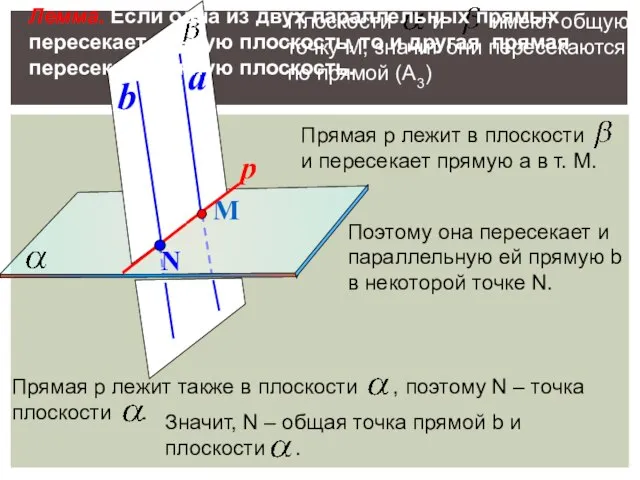
- 17. М a Поэтому она пересекает и параллельную ей прямую b в некоторой точке N. Лемма. Если
- 18. ПОВТОРИМ ПЛАНИМЕТРИЮ. Следствие из аксиомы параллельности. Аналогичное утверждение имеет место и для трех прямых в пространстве.
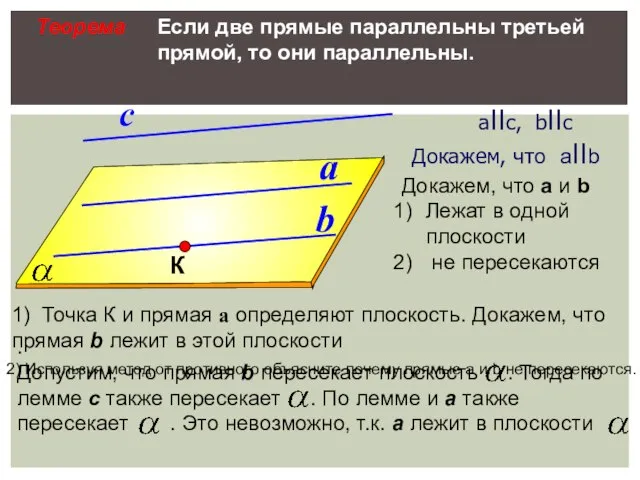
- 19. a b с Теорема Если две прямые параллельны третьей прямой, то они параллельны. aIIс, bIIс Докажем,
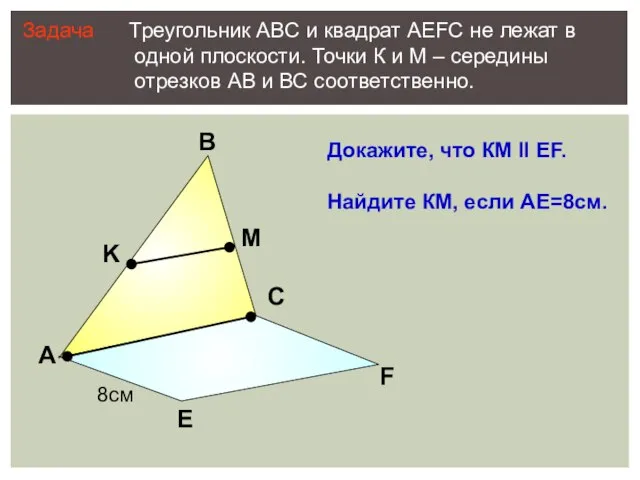
- 20. А В С Е F K M Задача Треугольник АВС и квадрат АEFC не лежат в
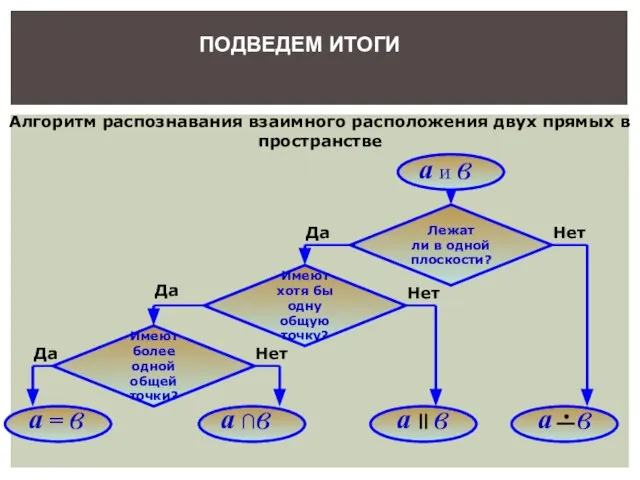
- 21. Алгоритм распознавания взаимного расположения двух прямых в пространстве Лежат ли в одной плоскости? Имеют хотя бы
- 22. Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые.
- 23. ДОМАШНЕЕ ЗАДАНИЕ П. 4, 5 теоремы Понятия: параллельность отрезков, отрезка и прямой, двух лучей в пространстве
- 25. Скачать презентацию






 Играем с Капитошкой. Игра-тренажёр по теме Таблица сложения
Играем с Капитошкой. Игра-тренажёр по теме Таблица сложения Виды треугольников. 5 класс
Виды треугольников. 5 класс Старинные меры длины на Руси
Старинные меры длины на Руси Первообразная функции
Первообразная функции Формулы. Повторение
Формулы. Повторение Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011
Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011 Системы счисления
Системы счисления Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения В мире геометрии
В мире геометрии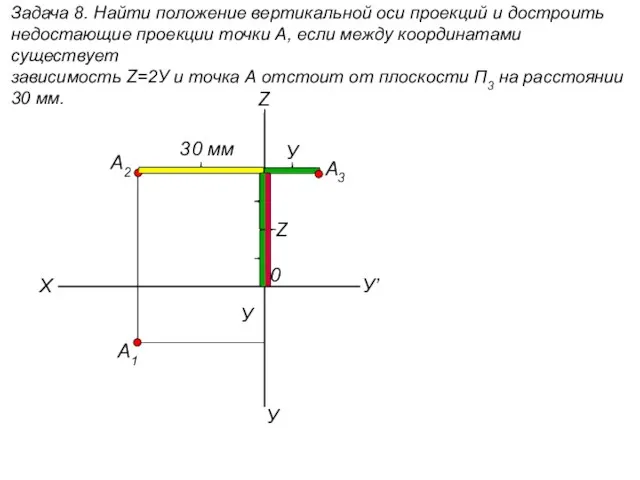 Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8)
Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8) Комбинаторика и теория вероятности
Комбинаторика и теория вероятности Односторонние пределы
Односторонние пределы Цилиндр в математике
Цилиндр в математике Презентация на тему Смежные углы
Презентация на тему Смежные углы  Геометрические тела и фигуры
Геометрические тела и фигуры Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс Реляционная алгебра
Реляционная алгебра Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Наименьшее и наибольшее значение функции. Задачи
Наименьшее и наибольшее значение функции. Задачи Равносильность уравнений. Линейные уравнения
Равносильность уравнений. Линейные уравнения Контрольна робота 1 (геометрія)
Контрольна робота 1 (геометрія) Метрология
Метрология Регулятивные удд
Регулятивные удд Кто что любит поесть?
Кто что любит поесть? Интеграл. Формула Ньютона-Лейбница. Что называют криволинейной трапецией?
Интеграл. Формула Ньютона-Лейбница. Что называют криволинейной трапецией? Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур