Содержание
- 2. Повторение Среди пар уравнений найдите пары равносильных:
- 3. Повторение Определите, какое из двух уравнений является следствие другого:
- 4. Повторение Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а ,
- 5. Что общего в этих уравнениях? =2 +
- 6. Иррациональные уравнения
- 7. Определение Иррациональными называются уравнения, в которых переменная содержится под знаком корня (радикала). Примеры:
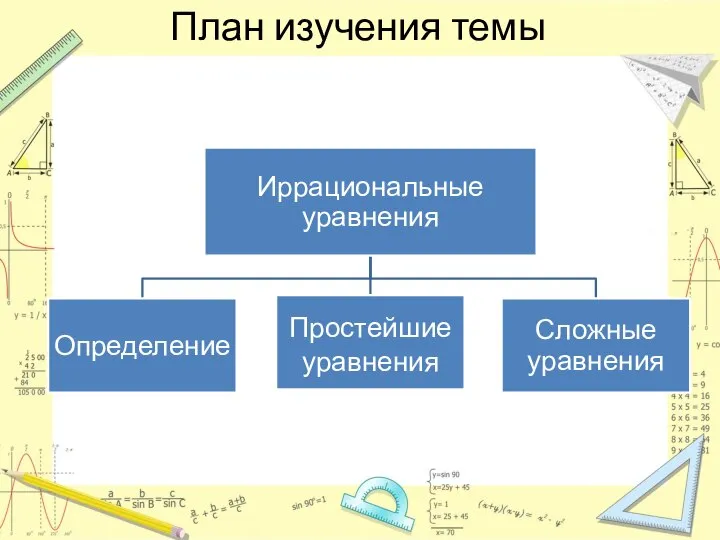
- 8. План изучения темы
- 9. Какие из уравнений не являются иррациональными?
- 10. Идея решения Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения
- 11. Простейшие иррациональные уравнения
- 12. Запомни! При возведении обеих частей уравнения • в четную степень (показатель корня – четное число) –
- 13. Запомни! Решая иррациональные уравнения с помощью равносильных преобразований (проверка не нужна)
- 14. Решение уравнения 1) а Пример: 2) а=0, то Пример: 3) a>0, то Пример:
- 15. Решение уравнения 1 способ 2 способ
- 16. Вывод Уравнение вида решается: Возведением в квадрат обеих частей равенства с последующей проверкой; Осуществляется переход к
- 17. Решение уравнения 1 способ 2 способ
- 18. Вывод Уравнение вида решается: Возведением в квадрат обеих частей равенства с последующей проверкой; Осуществляется переход к
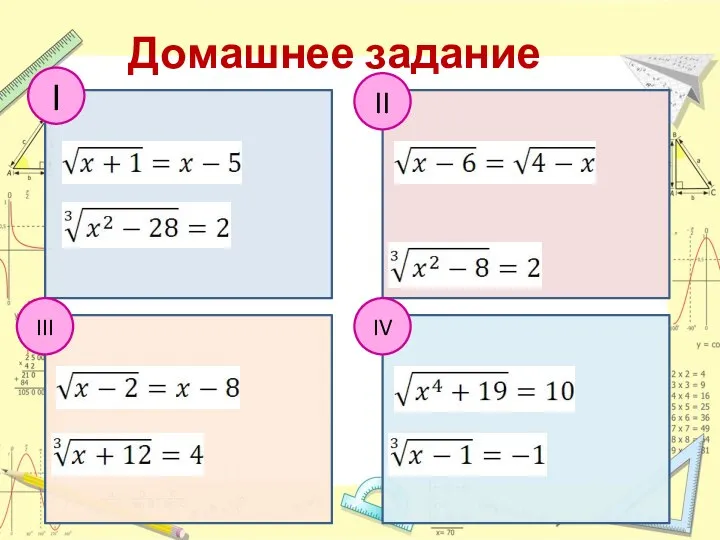
- 19. Домашнее задание I III II IV
- 21. Скачать презентацию
















 Математика. Решение задач
Математика. Решение задач Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Решение неравенств. ЕГЭ, задание 15
Решение неравенств. ЕГЭ, задание 15 Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Умножение десятичных дробей
Умножение десятичных дробей Применение преобразований графиков функций
Применение преобразований графиков функций Первообразная функции
Первообразная функции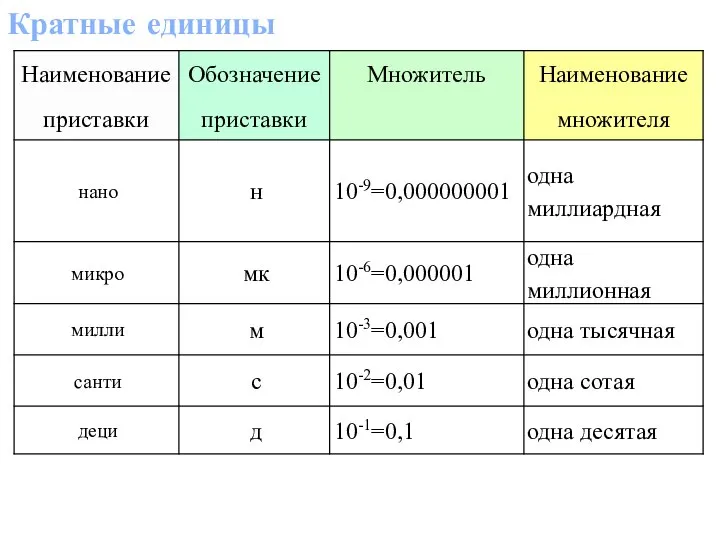 Кратные единицы
Кратные единицы Математические иллюзии
Математические иллюзии Параллельные прямые
Параллельные прямые Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Методы решения творческих задач
Методы решения творческих задач Обыкновенные дроби. Основное свойство дроби. 5 класс
Обыкновенные дроби. Основное свойство дроби. 5 класс Точки экстремума. Промежутки возрастания и убывания функции
Точки экстремума. Промежутки возрастания и убывания функции координаты вектора
координаты вектора Основное тригонометрическое тождество и его следствия
Основное тригонометрическое тождество и его следствия Древнекитайское доказательство
Древнекитайское доказательство Задачи на проценты
Задачи на проценты Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Программа по математике для начальной школы в соответствии с ФГОС - 2
Программа по математике для начальной школы в соответствии с ФГОС - 2 Презентация на тему Двугранный угол (10 класс)
Презентация на тему Двугранный угол (10 класс)  Геометрическое место точек. 7 класс
Геометрическое место точек. 7 класс Проценты. Графический диктант
Проценты. Графический диктант Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Сложение и вычитание трёхзначных чисел. Геометрическое задание
Сложение и вычитание трёхзначных чисел. Геометрическое задание Проценты
Проценты Погрешность прямых измерений
Погрешность прямых измерений Классификация функций
Классификация функций