Содержание
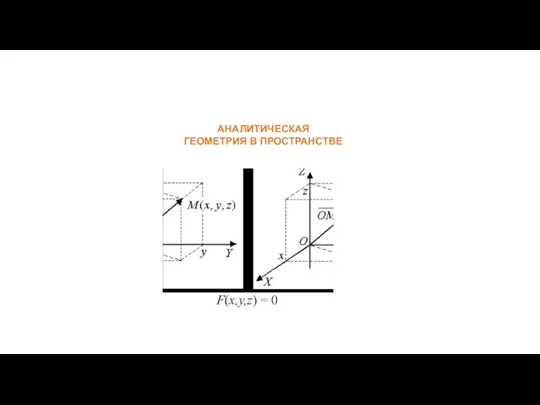
- 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ F(x,y,z) = 0
- 3. Расстояние между двумя точками. Деление отрезка в данном отношении Координаты середины отрезка
- 4. 1. Плоскость в пространстве
- 5. Плоскость в пространстве и ее уравнения 1) Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- 6. Пример. Составьте уравнение плоскости, проходящей через точку M(1;1;1) перпендикулярно к вектору N={2;2;3}. Решение:
- 7. 3) Уравнение плоскости в отрезках на осях здесь числа представляют собой отрезки, отсекаемые плоскостью на координатных
- 8. Задача. Какие отрезки отсекает на осях координат плоскость 2x – 4y + 6z –12 = 0
- 9. 4) Уравнение плоскости, проходящей через три данные точки Даны три точки: – произвольная точка плоскости. Точка
- 10. 5) Нормальное уравнение плоскости
- 11. Приведение общего уравнения плоскости к нормальному уравнению
- 12. А=0: By + Cz + D = 0 (отсутствует переменная х) – плоскость параллельна оси Ох;
- 13. Условие перпендикулярности и параллельности плоскостей π1 ⊥π2 , если N1 ⊥ N2 (Критерий ортогональности: скалярное произведение
- 14. Пример. Составить уравнение плоскости, которая проходит через точку M(7,-2, 3) параллельно плоскости y – 3z +
- 15. Пример. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: x – y
- 16. 1 способ: 2 способ: Подставляя координаты точки (по условию – начало координат (0,0,0)) и координаты нормального
- 17. Если два уравнения определяют одну и ту же плоскость, то коэффициенты их пропорциональны Условие совпадения (слияния)
- 18. Угол между плоскостями Один из двугранных углов между плоскостями равен острому углу между их нормальными векторами
- 19. Пример. Найти угол между плоскостями
- 20. Расстояние от точки до плоскости Расстояние между двумя параллельными плоскостями
- 21. Пример
- 22. Прямая в пространстве
- 23. 1) Общие уравнения прямой в пространстве 2) Канонические уравнения прямой в пространстве a = {m;n;p} –
- 24. Пример. Составьте канонические и параметрические уравнения прямой Решение. 1) Находим координаты точки, лежащей на прямой. Для
- 25. 2) Находим направляющий вектор прямой: 3) Канонические уравнения прямой: Параметрические уравнения прямой:
- 26. 4) Уравнение прямой в пространстве, проходящей через две данные точки и - известные точки на прямой;
- 27. Пример. Составьте уравнение прямой, проходящей через две точки и Решение
- 28. Пример.
- 29. Решение. Прямые задаются пересечением плоскостей: Направляющие векторы прямых:
- 31. условие параллельности прямых: условие перпендикулярности прямых условие того, что прямые лежат в одной плоскости Взаимное расположение
- 32. расстояние от точки М1 до прямой, проходящей через точку М0 расстояние между двумя прямыми в пространстве
- 33. ПРЯМАЯ И ПЛОСКОСТЬ
- 34. Точка пересечения прямой и плоскости Пример. Найдите точку пересечения прямой и плоскости Решение. 1) Запишем уравнение
- 35. 2) Подставим выражения для переменных x, y, z в уравнение плоскости и найдем значение параметра t
- 37. Если угол Ψ острый, то ; если угол Ψ тупой, то , то есть .
- 38. Взаимное расположение прямой и плоскости в пространстве условие параллельности ⎢⎢π ⇔ условие того, что прямая принадлежит
- 40. Скачать презентацию




































 Числовые последовательности
Числовые последовательности Презентация на тему Тренажер по математике 2 класс
Презентация на тему Тренажер по математике 2 класс  Уравнение сферы
Уравнение сферы Задачи на готовых чертежах по теме Подобие
Задачи на готовых чертежах по теме Подобие Площади. Теорема Пифагора. Урок - зачёт 8 класс
Площади. Теорема Пифагора. Урок - зачёт 8 класс Интеграл
Интеграл По следам теоремы Пифагора
По следам теоремы Пифагора Математика в мире животных и животные в математике
Математика в мире животных и животные в математике Тела вращения в природе
Тела вращения в природе Перпендикулярность плоскостей
Перпендикулярность плоскостей Дифуры 1 порядка
Дифуры 1 порядка Нематематики о математике
Нематематики о математике Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Деление окружности на 5 равных частей. Сопряжение
Деление окружности на 5 равных частей. Сопряжение Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Решение уравнений с одной переменной
Решение уравнений с одной переменной Правильные многогранникик
Правильные многогранникик Признаки равенства треугольников
Признаки равенства треугольников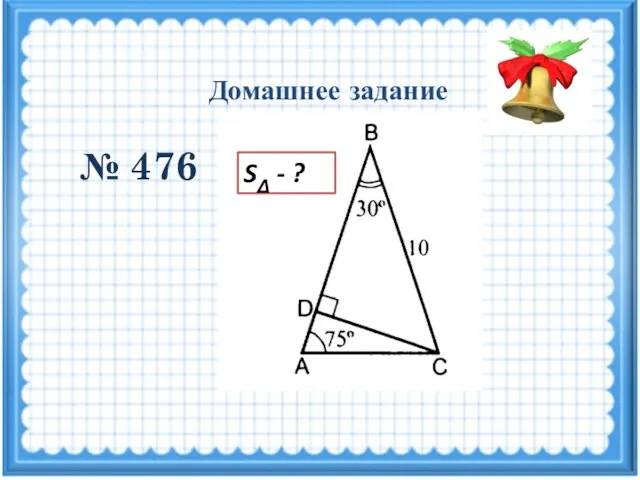 Домашнее задание № 476
Домашнее задание № 476 Сумма углов треугольника
Сумма углов треугольника Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний
Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний Презентация на тему Решение квадратных уравнений и неравенств
Презентация на тему Решение квадратных уравнений и неравенств  Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Средняя линия треугольника
Средняя линия треугольника Презентация на тему КВН. Математика повсюду
Презентация на тему КВН. Математика повсюду  Корень уравнения
Корень уравнения Задачи на проценты. ОГЭ
Задачи на проценты. ОГЭ