Аксиомы стереометрии

Цели:
Ознакомить учащихся с содержанием курса стереометрии
Изучить аксиомы стереометрии и их использование при решении задач

- Что такое геометрия?
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости.
А
а
Основные понятия планиметрии:
точка
прямая
- Основные понятия планиметрии?

Стереометрия
- раздел геометрии, в котором изучаются свойства фигур в пространстве

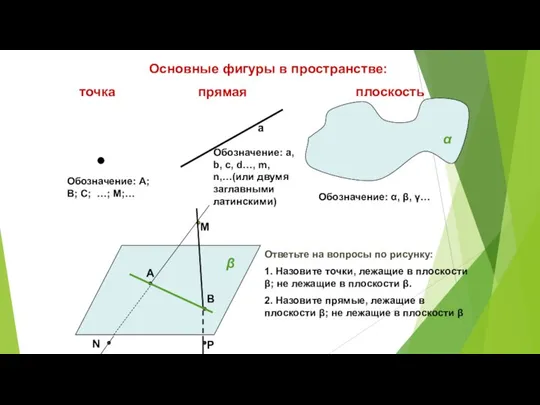
Основные фигуры в пространстве:
точка прямая плоскость
α
β
Обозначение: А; В; С; …; М;…
а
А
В
М
N
Р
Обозначение: a, b, с, d…, m, n,…(или двумя заглавными латинскими)
Обозначение: α, β, γ…
Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β; не лежащие в плоскости β.
2. Назовите прямые, лежащие в плоскости β; не лежащие в плоскости β

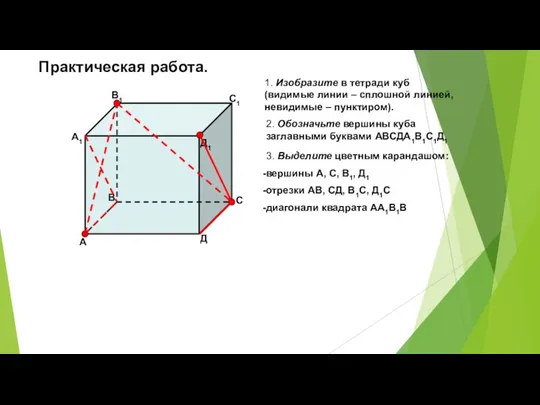
Практическая работа.
1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром).
2. Обозначьте вершины куба заглавными буквами АВСДА1В1С1Д1
А
В
С
Д
Д1
С1
В1
А1
3. Выделите цветным карандашом:
вершины А, С, В1, Д1
отрезки АВ, СД, В1С, Д1С
диагонали квадрата АА1В1В

- Что такое аксиома?
Аксиома – это утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.
Аксиомы планиметрии:
- через любые две точки можно провести прямую и притом только одну.
из трех точек прямой одна, и только одна, лежит между двумя другими.
имеются по крайней мере три точки, не лежащие на одной прямой…

Аксиомы стереометрии
А1. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии

Аксиомы стереометрии.
А
В
С
А2. (аксиома плоскости) Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.
α

Коллинеарные и неколлинеарные точки
Три точки, принадлежащие одной прямой, называются коллинеарными, а три точки, не принадлежащие одной прямой, - неколлинеарными.
!!! Три неколлинеарные точки в пространстве определяют плоскость!!!

Аксиомы стереометрии
А3. Какова бы ни была плоскость, существуют точки принадлежащие этой плоскости, и точки не принадлежащие ей.

Аксиомы стереометрии.
А
В
α
А4. ( аксиома прямой и плоскости) Если две точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости.
Говорят: прямая лежит в плоскости или плоскость проходит через прямую.

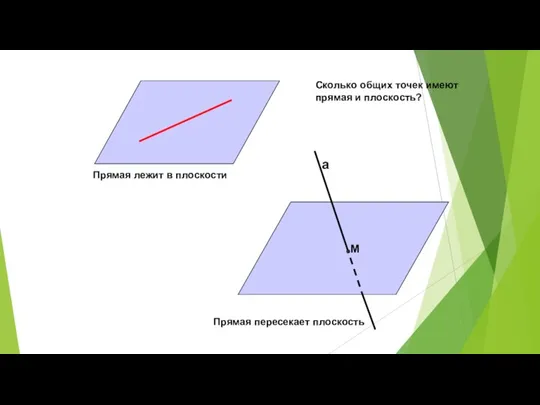
а
М
Прямая лежит в плоскости
Прямая пересекает плоскость
Сколько общих точек имеют прямая и плоскость?

Определение!!!
Прямая и плоскость, имеющие ровно одну общую точку, называются пересекающимися.

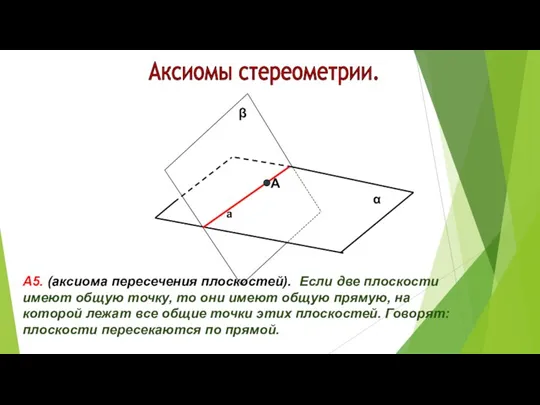
Аксиомы стереометрии.
α
β
А5. (аксиома пересечения плоскостей). Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят: плоскости пересекаются по прямой.
А
а

а
М
Аксиомы стереометрии
А6. ( Аксиома разбиения пространства)
Любая плоскость разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что
А) любые две точки, принадлежащие разным множествам разделены плоскостью.
Б) любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью.
В
С

Аксиомы стереометрии
А7. ( Аксиома расстояния) Расстояние между любыми двумя точками пространства одно и тоже на любой плоскости, проходящей через эти точки.

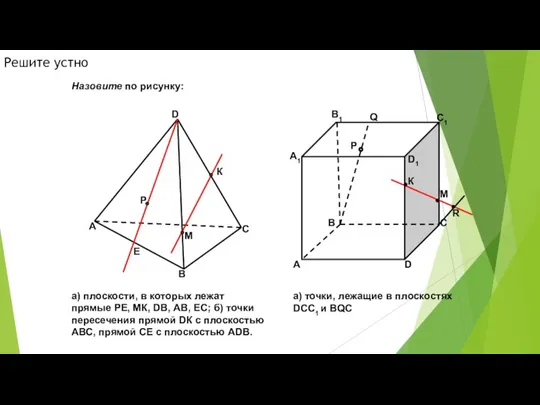
А
В
С
D
Р
Е
К
М
А
В
С
D
А1
В1
С1
D1
Q
P
R
К
М
Назовите по рисунку:
а) плоскости, в которых лежат прямые РЕ, МК, DВ, АВ, ЕС; б) точки пересечения прямой DК с плоскостью АВС, прямой СЕ с плоскостью АDВ.
а) точки, лежащие в плоскостях DСС1 и ВQС
Решите устно

Работаем с учебником!
Задачник стр.7-8
№ 1.007;
1.008;
1.009;
1.011.