Содержание
- 2. Цель: Изучить функцию y = tg x Задачи: 1. Изучить свойства функции у = tg x.
- 3. Функция y=tgx определена при x ≠ π/2+πn, n∈Z, является нечётной и периодической с периодом Т=π Поэтому
- 4. Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π/2] Мы получили график функции на заданном
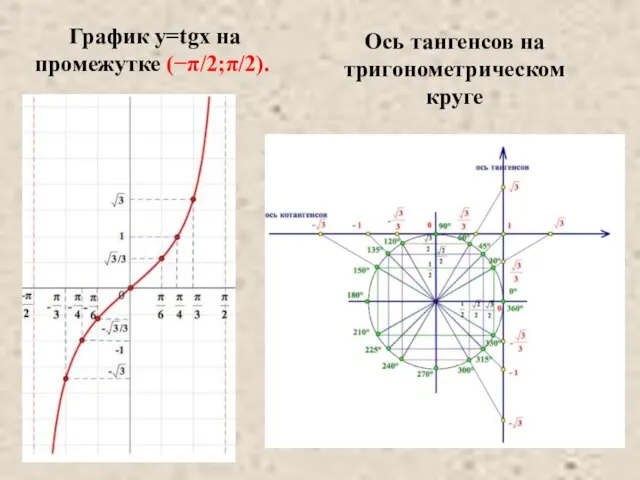
- 5. Ось тангенсов на тригонометрическом круге График y=tgx на промежутке (−π/2;π/2).
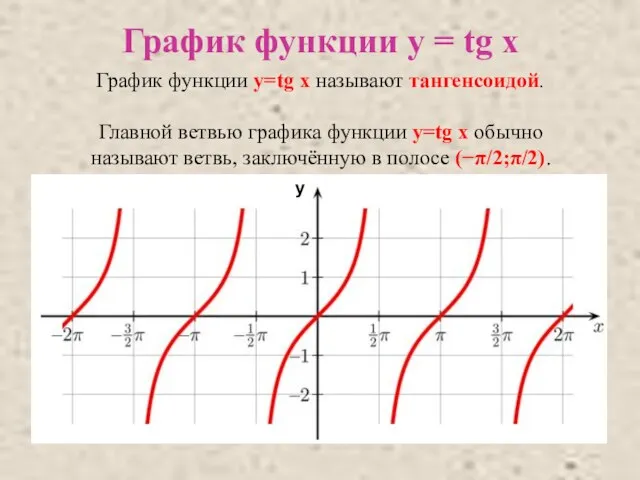
- 6. График функции y=tg x называют тангенсоидой. Главной ветвью графика функции y=tg x обычно называют ветвь, заключённую
- 7. Свойства функции y = tg x 1. Область определения — множество R всех действительных чисел. D(y)
- 8. 8. Промежутки, на которых функция принимает положительные значения при x ∈ (πn; π/2+πn), n ∈ Z
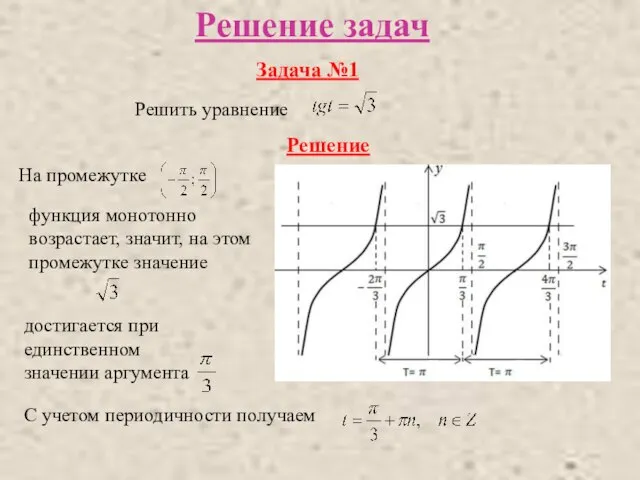
- 9. Решение задач Решить уравнение Задача №1 Решение На промежутке функция монотонно возрастает, значит, на этом промежутке
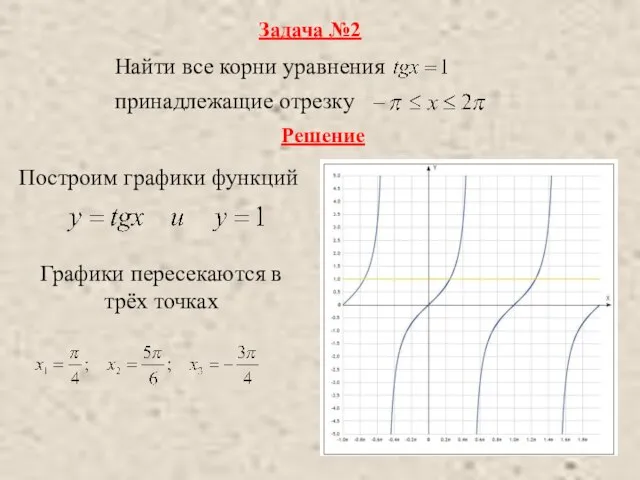
- 10. Задача №2 Найти все корни уравнения принадлежащие отрезку Решение Построим графики функций Графики пересекаются в трёх
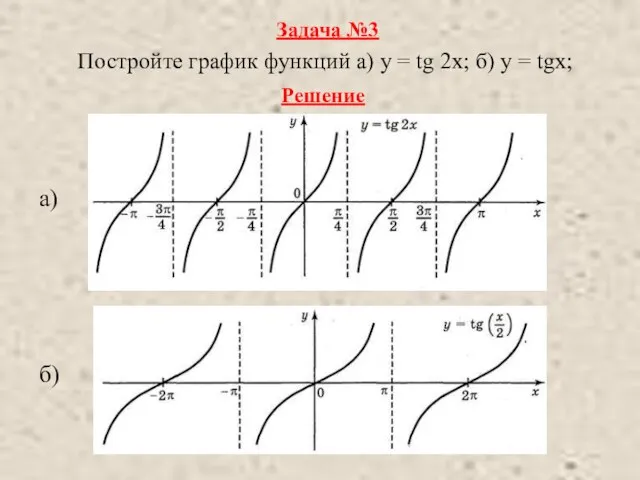
- 11. Задача №3 Постройте график функций а) у = tg 2х; б) у = tgx; Решение а)
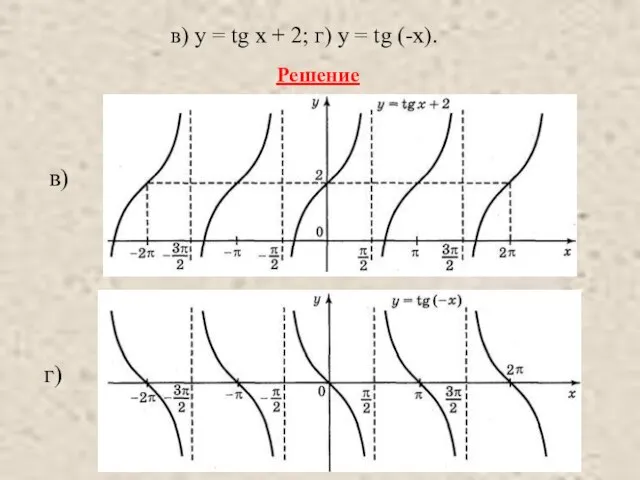
- 12. в) у = tg x + 2; г) у = tg (-x). Решение в) г)
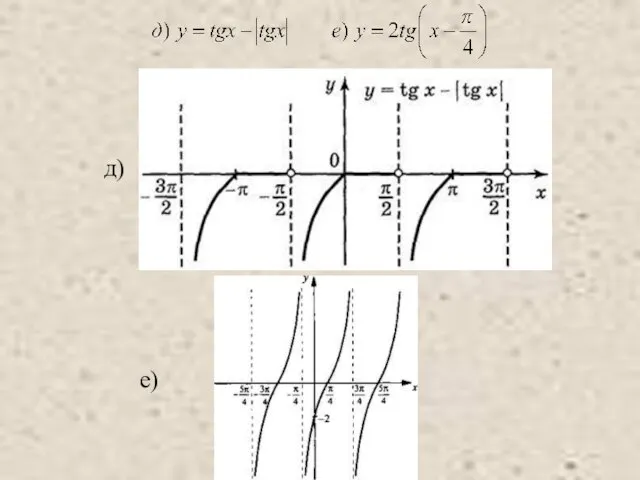
- 13. е) д)
- 14. Задача №4 Установить чётность или нечётность функции Решение Так как выполнено равенство y(-x) = у(х), то
- 15. Задания для самостоятельного решения 1) Постройте графики функций а) у = tg(x+ π/3); б) у =
- 16. 2) Определить чётность или нечётность функции:
- 17. 3) Решить графически уравнения:
- 18. 4) Используя свойства функции у = tg x, сравните числа: 5) Используя свойства функции у =
- 20. Скачать презентацию


![Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π/2] Мы получили](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851695/slide-3.jpg)







 Симметрия в пространстве
Симметрия в пространстве Оптимизация по методу Бокса-Уилсона
Оптимизация по методу Бокса-Уилсона Прямоугольник. Теоремы
Прямоугольник. Теоремы Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Умножение десятичной дроби на единицу с нулями
Умножение десятичной дроби на единицу с нулями Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Вписанная окружность
Вписанная окружность Многогранники. Стереометрия
Многогранники. Стереометрия Правильный многоугольник
Правильный многоугольник Окружность и круг
Окружность и круг Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Задачи на умножение
Задачи на умножение Случайные величины
Случайные величины Равенство векторов
Равенство векторов Графы
Графы Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Счет до 10
Счет до 10 Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Упражнения
Упражнения Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Решение задач на нахождение зависимости между величинами используя графики
Решение задач на нахождение зависимости между величинами используя графики График функции
График функции Математический диктант
Математический диктант Применение векторов к решению задач (9 класс)
Применение векторов к решению задач (9 класс) Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах Numbers and animals
Numbers and animals Свойства функций
Свойства функций Умножение обыкновенных дробей
Умножение обыкновенных дробей