Центральные и вписанные углы

●
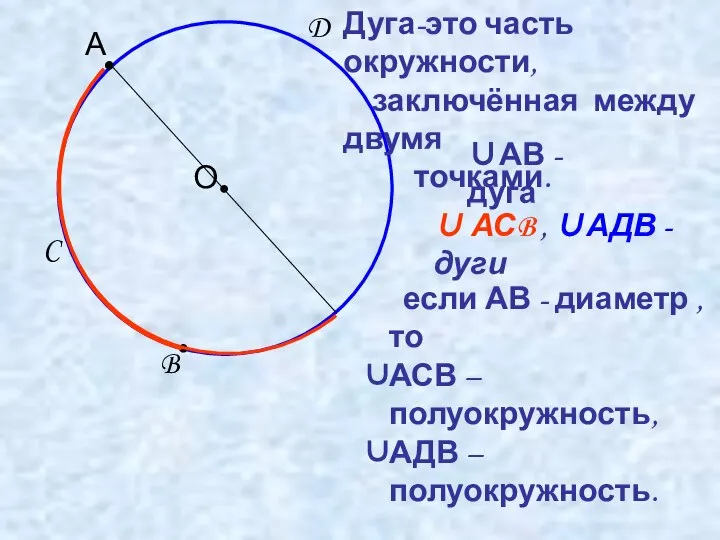
О
А
B
C
D
если АВ - диаметр , то
АСВ – полуокружность,
АДВ – полуокружность.
Дуга-это часть окружности,
заключённая между двумя
точками.
∪ АСB , ∪АДВ - дуги
∪АВ - дуга
●
●

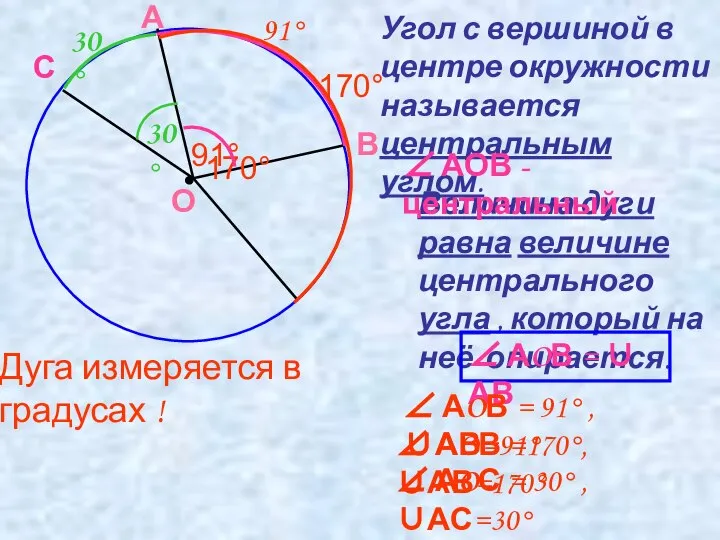
Угол с вершиной в центре окружности называется центральным углом.
О
А
В
170°
170°
Величина дуги равна величине центрального угла , который на неё опирается.
∠ АОВ - центральный
Дуга измеряется в градусах !
91°
∠ АOВ = ∪ АВ
●
91°
∠ АOВ = 91° ,∪АВ=91°
∠ АOВ =170°,∪АВ=170°
∠ АOС = 30° ,∪АС=30°
С
30 °
30°

●
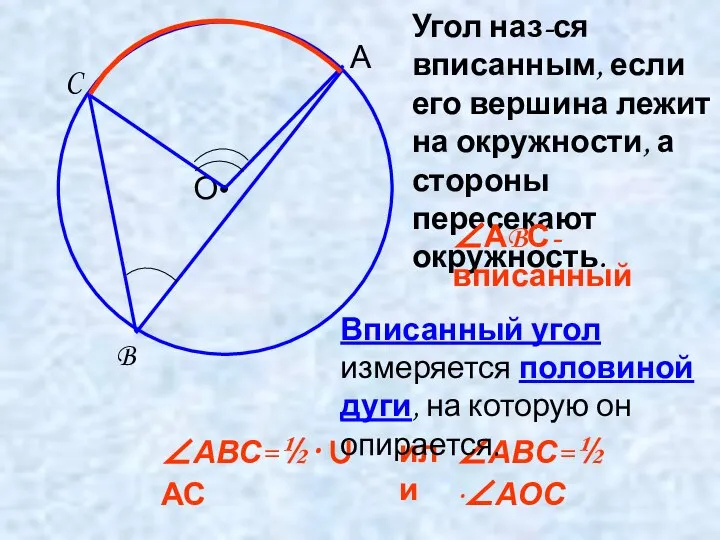
О
А
B
C
или
∠АВС=½ ·∠АОС
Угол наз-ся вписанным, если его вершина лежит на окружности, а стороны пересекают окружность.
∠АBС-вписанный
∠АВС=½· ∪ АС
Вписанный угол измеряется половиной дуги, на которую он опирается.

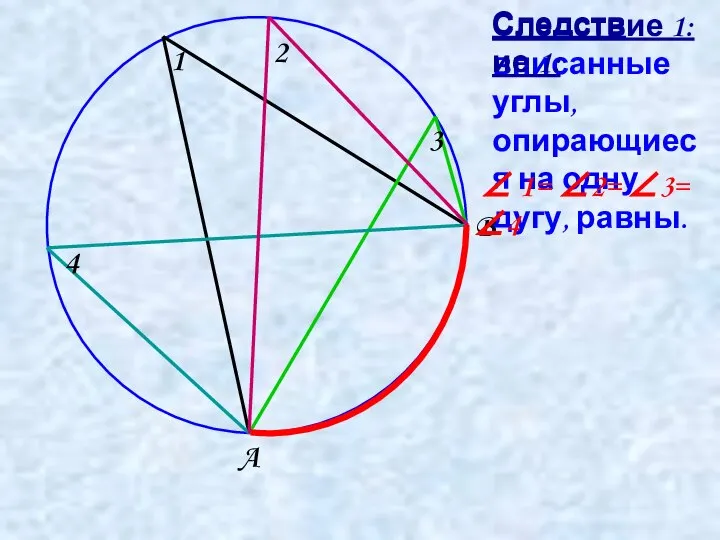
Следствие 1: вписанные углы, опирающиеся на одну дугу, равны.
A
B
∠ 1= ∠2= ∠3= ∠4
1
3
2
4
Следствие 1:

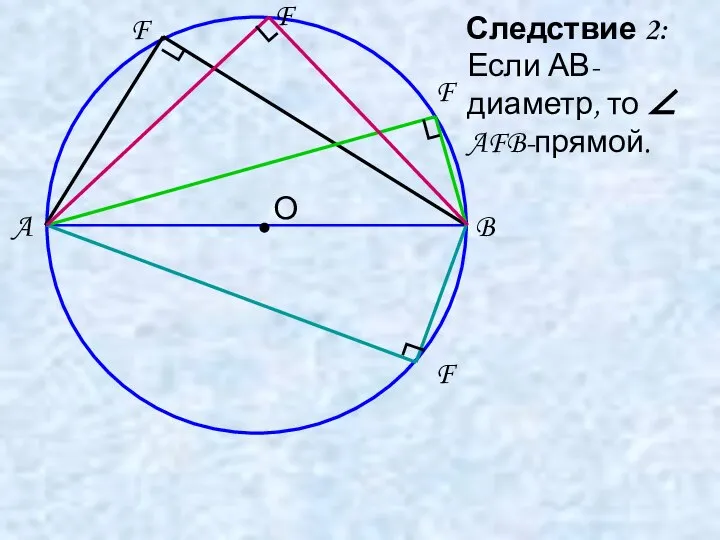
Следствие 2:
A
B
Если АВ-диаметр, то ∠ AFB-прямой.
F
F
F
F
┐
┐
┐
┐
•
О

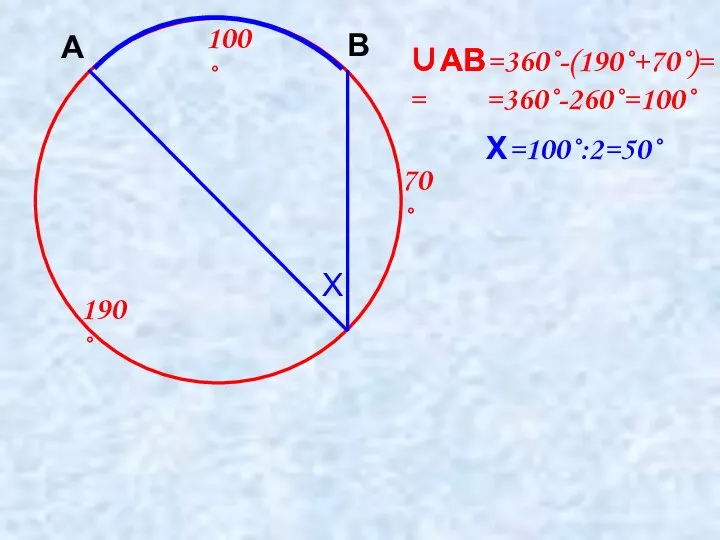
190˚
Х
70˚
А
В
∪АВ=360˚-(190˚+70˚)=
=360˚-260˚=100˚
100˚
Х=100˚:2=50˚
∪АВ=

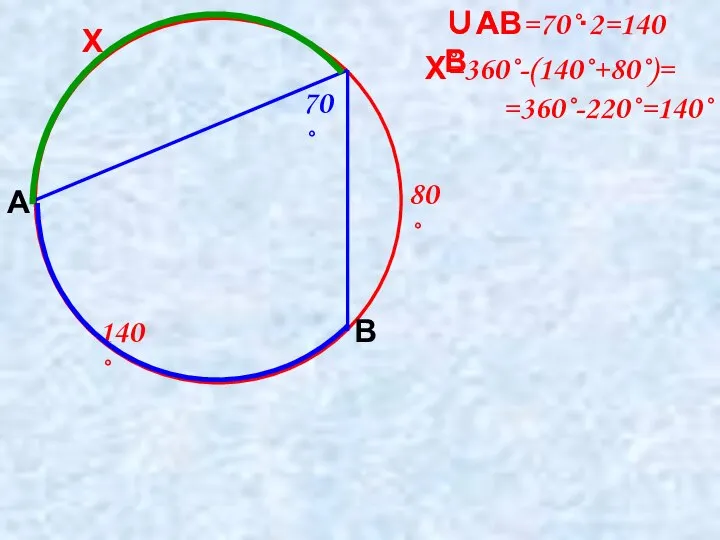
80˚
Х
70˚
А
В
Х=360˚-(140˚+80˚)=
=360˚-220˚=140˚
∪АВ=70˚∙2=140˚
∪АВ
140˚