Параллелограм и трапеция

Параллелограмм
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.

Признаки параллелограмма
Первый признак параллелограмма.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм.
AB||CD, AB=CD,значит
ABCD-параллелограмм

Доказательство 1-го признака параллелограмма

Признаки параллелограмма
2. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны, то этот четырехугольник – параллелограмм.
AB=CD,
AD=BC,
значит ABCD-параллелограмм

Доказательство 2-го признака параллелограмма

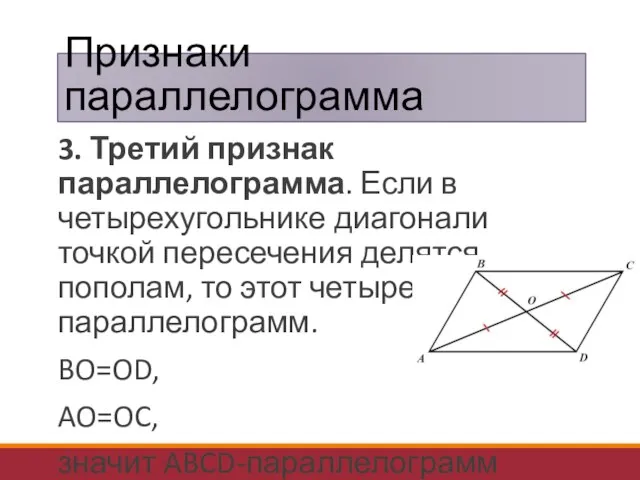
Признаки параллелограмма
3. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
BO=OD,
AO=OC,
значит ABCD-параллелограмм

Доказательство 3-го признака параллелограмма

Основные свойства параллелограмма
1. Противоположные стороны параллелограмма имеют одинаковую длину:
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма равны:
∠ABC = ∠CDA, ∠BCD = ∠DAB

Дано:
ABCD — параллелограмм.
Доказать:
AB=CD, AD=BC,
∠A=∠C, ∠B=∠D.

Рассмотрим треугольники ABD и CDB.
1) сторона BD — общая
2) ∠ABD=∠CDB (как внутренние накрест лежащие при AB∥CD и секущей BD)
3) ∠ADB=∠CBD (как внутренние накрест лежащие при AD∥BC и секущей BD)
Значит, ∆ABD= ∆CDB (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AB=CD, AD=BC
и равенство соответствующих углов: ∠A=∠C.
В пунктах 2) и 3) обосновано, что ∠ABD=∠CDB и ∠ADB=∠CB.
Следовательно,
∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,
то есть, ∠B=∠D.
Что и требовалось доказать.

Основные свойства параллелограмма
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

Свойство непосредственно вытекает из того, что углы, прилежащие к одной стороне параллелограмма, являются внутренними односторонними углами при параллельных прямых.
Для параллелограмма ABCD:
∠A+∠B=180º (как внутренние односторонние при AD∥BC и секущей AB;
∠C+∠D=180º (как внутренние односторонние при AD∥BC и секущей CD;
∠A+∠D=180º (как внутренние односторонние при AB∥CD и секущей AD;
∠B+∠C=180º (как внутренние односторонние при AB∥CD и секущей BC.

Основные свойства параллелограмма
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали d1 ,d2 параллелограмма и стороны
a,b связаны следующим
соотношением: d12+d22=2(a2+b2)

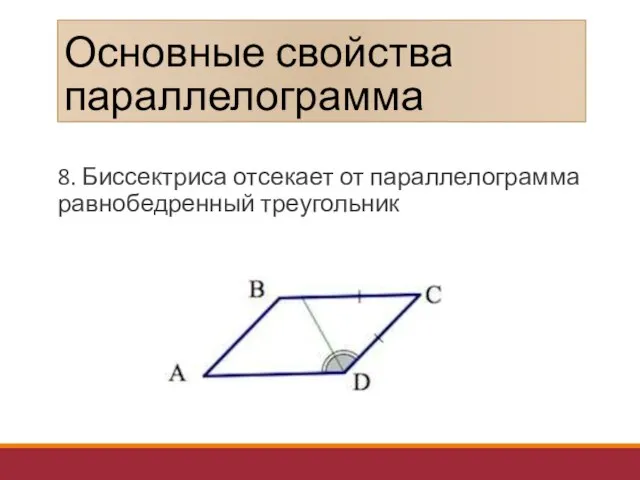
Основные свойства параллелограмма
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник

Основные свойства параллелограмма
9. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:AC2 + BD2 = 2AB2 + 2BC2
10. Биссектрисы противоположных углов параллелограмма всегда параллельны
11. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)

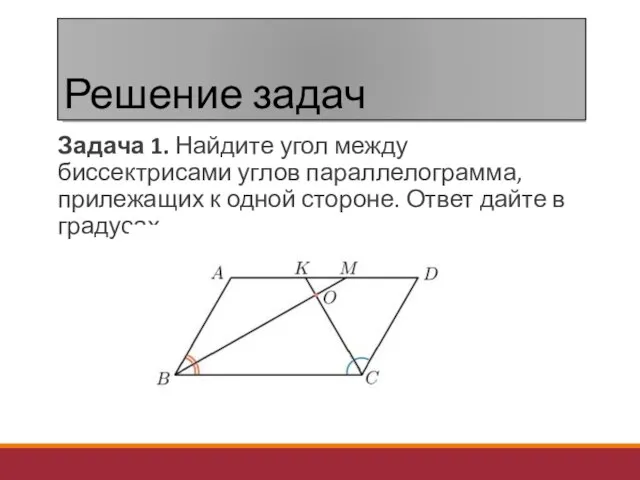
Решение задач
Задача 1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Решение задач
Решение.
1.Пусть BM и CK — биссектрисы углов параллелограмма, прилежащих к стороне BC.
2. Сумма углов ABC и BCD равна 180°.Углы OBC и OCB — половинки углов ABC и BCD. Значит, сумма углов ABC и BCD равна 90° градусов. Из треугольника BOC находим, что угол BOC— прямой.
Ответ: 90°.

Решение задач
Задача 2.
Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Решение задач
Решение.
Пусть ∠А = х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение:
х + 3х = 180;
4х = 180;
х = 180 : 4;
х = 45.
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Трапеция
Трапеция — выпуклый четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Параллельные стороны называют основаниями, а две другие — боковыми сторонами.

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полсумме:
m = (a + b)/2
2. Средняя линия трапеции разделяет пополам любой отрезок который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Биссектриса любого угла трапеции отсекает
на её основании (или продолжении)
отрезок, равный боковой стороне.

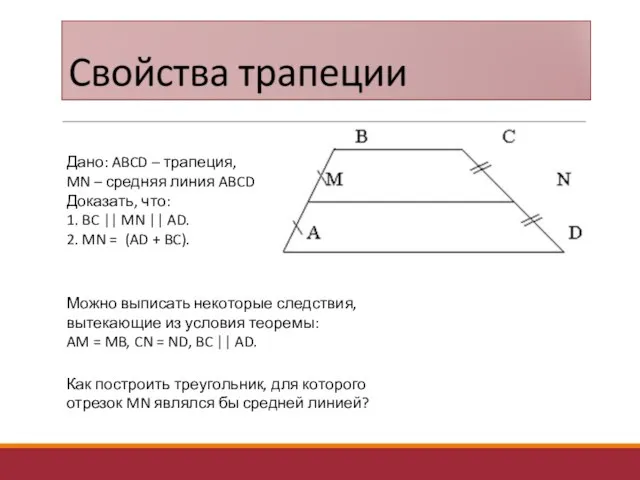
Дано: ABCD – трапеция,
MN – средняя линия ABCD
Доказать, что:
1. BC || MN || AD.
2. MN = (AD + BC).
Можно выписать некоторые следствия, вытекающие из условия теоремы:
AM = MB, CN = ND, BC || AD.
Как построить треугольник, для которого отрезок MN являлся бы средней линией?

Доказательство :
1. Рассмотрим BNC и DNK, в них:
а) ∟CNB = ∟DNK (свойство вертикальных углов);
б) ∟BCN = ∟NDK (свойство внутренних накрест лежащих углов);
в) CN = ND (по следствию из условия теоремы).
Значит BNC = DNK (по стороне и двум прилежащим к ней углам).
1. Из равенства BNC = DNK следует, что BN = NK, а значит MN – средняя линия ABK.
2. MN || AD (п. 2).
3. Так как ABCD – трапеция, то BC||AD, но MN || AD, значит BC || MN || AD.
4. MN = AK, но AK = AD + DK, причём DK = BC
(BNC = DNK), значит MN = (AD + BC).
Что и требовалось доказать.

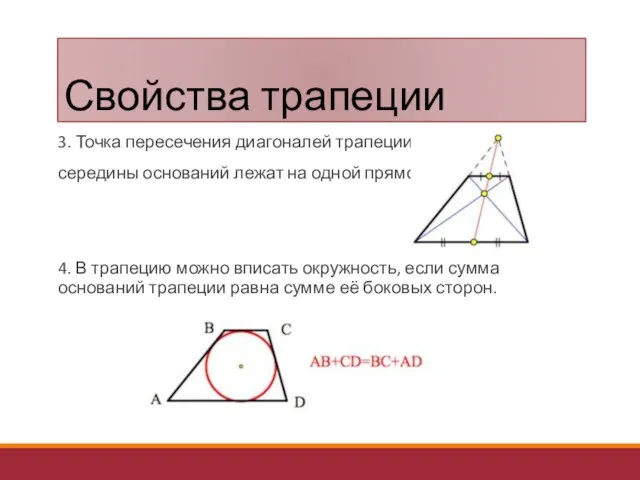
Свойства трапеции
3. Точка пересечения диагоналей трапеции и
середины оснований лежат на одной прямой.
4. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

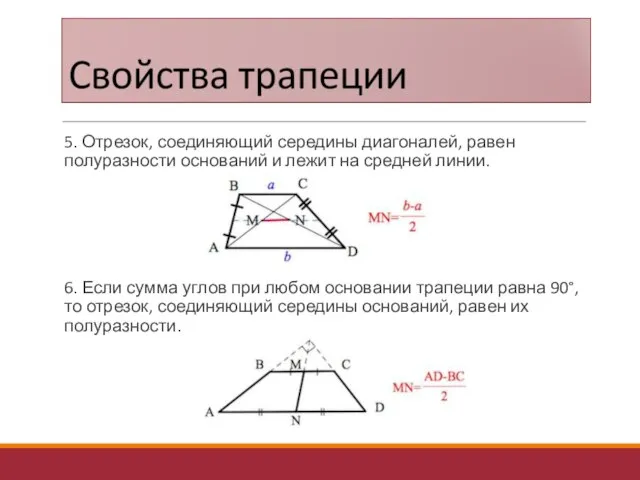
5. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
6. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

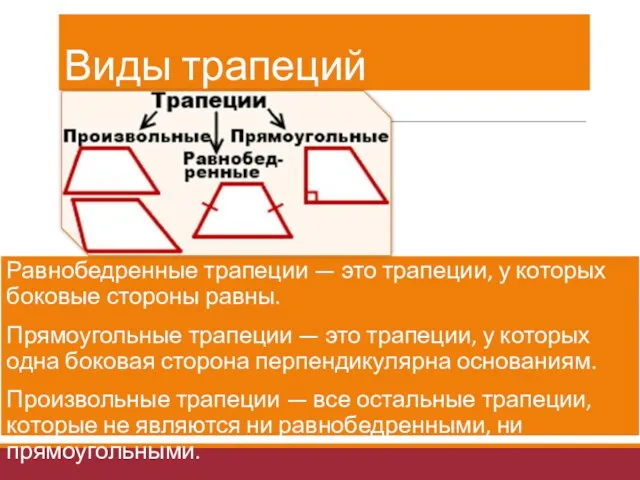
Виды трапеций
Равнобедренные трапеции — это трапеции, у которых боковые стороны равны.
Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям.
Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными.

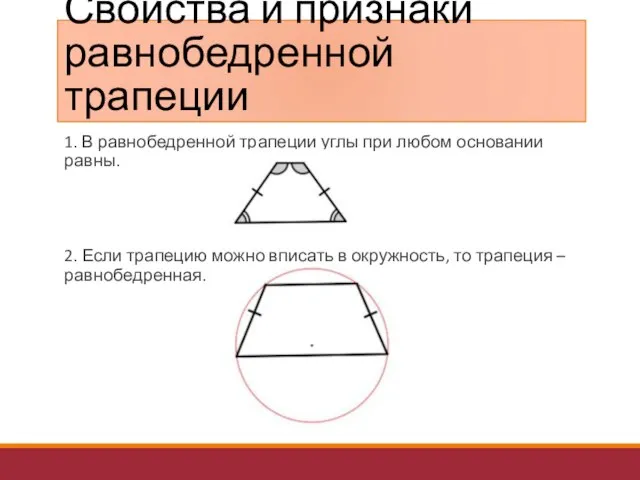
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

Свойства и признаки равнобедренной трапеции
3. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.