Содержание
- 2. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения. Проверяемую гипотезу называют нулевой
- 3. Правильное решение Ошибка 1-го рода Ошибка 2-го рода Правильное решение
- 4. 1. 2. Строим случайную величину K, называемую ста-тистическим критерием, для которой выполня- ются следующие условия: она
- 5. 3. Вычисляем значения критерия, подставляя в него выборочные данные. Это число называют наблю-даемым значением критерия и
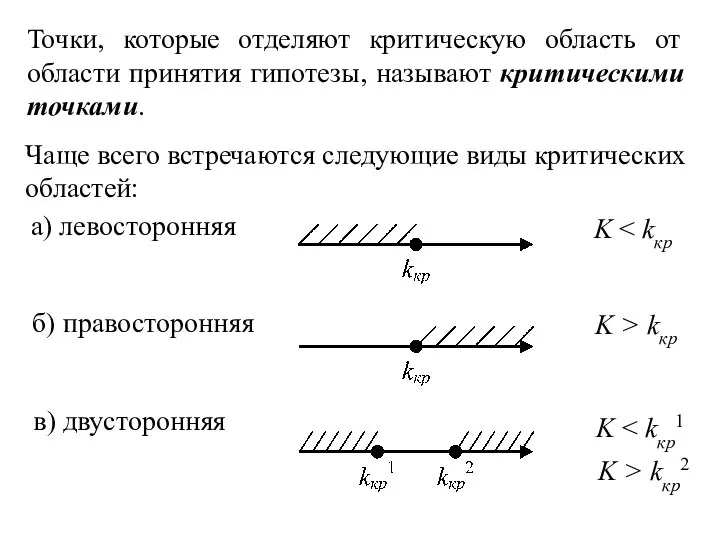
- 6. Точки, которые отделяют критическую область от области принятия гипотезы, называют критическими точками. Чаще всего встречаются следующие
- 7. Критическую область W целесообразно находить согласно следующим требованиям: 1. 2. Мощность критерия – максимальная.
- 8. При разработке статистического критерия невозможно одновременно минимизировать обе ошибки. Поэтому поступают следующим образом: при заданном числе
- 10. Пять шагов проверки гипотезы 1. Сформулировать нулевую H0 и альтернативную H1 гипотезы. 2. Выбрать статистику критерия
- 11. H0: генеральная совокупность имеет некоторое определённое распределение Параметрические критерии тестируют гипотезы о параметрах некоторого распределения :
- 12. § Критерий согласия Колмогорова Нулевая гипотеза: исследуемая случайная величина имеет заданный закон распределения. F(x) – теоретическая
- 14. Можно доказать, что при
- 16. § Критерий согласия Пирсона (хи-квадрат) Найдём теоретические частоты вариант. 1. Распределение дискретное p(x). Теоретическая частота появления
- 17. Критерий: ni – эмпирические частоты npi – теоретические частоты k = l – r –1, l
- 18. Критическая область W – правосторонняя: Из требования для критической области: F(x) – функция распределения Пирсона с
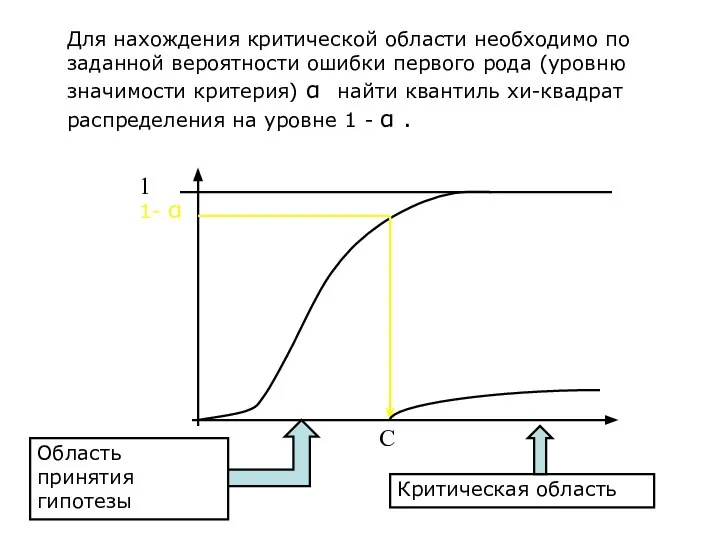
- 19. Для нахождения критической области необходимо по заданной вероятности ошибки первого рода (уровню значимости критерия) α найти
- 20. Алгоритм применения критерия согласия Пирсона Подсчитываем значение статистики критерия и сравниваем его с критической точкой. Если
- 21. § Критерий Фишера Две генеральные совокупности X и Y распределены нормально. Проверить гипотезу: Критерий: F имеет
- 22. 1. Критическая область W – правосторонняя: Из требования 1 для критической области: F(x) – функция распределения
- 23. 2. Обозначим , F’ имеет распределение Фишера с (nY –1) и (nX –1) степенями свободы предыдущий
- 24. , тогда Таким образом, критическая область для критерия F имеет вид: , где F(x) – функция
- 25. 3. Критическая область W – двусторонняя: Аналогично пунктам 1 и 2 получаем: где F1(x) – функция
- 26. § Критерий Стьюдента (t-критерий) Генеральная совокупность распределена нормально. Проверить гипотезу: a0 – некоторое число Критерий: Т
- 27. 1. Критическая область W – правосторонняя: Из требования 1 для критической области: F(x) – функция распределения
- 28. 2. Критическая область W – левосторонняя: Из требования 1 для критической области: , F(x) – функция
- 29. Плотность распределения Стьюдента – чётная функция Критическая точка tпр,кр находится из требования: –tпр,кр является критической точкой
- 30. 3. Критическая область W – двусторонняя: В силу чётности плотности распределения Стьюдента: Аналогично пунктам 1 и
- 31. 2. Обозначим , F’ имеет распределение Фишера с (nY –1) и (nX –1) степенями свободы предыдущий
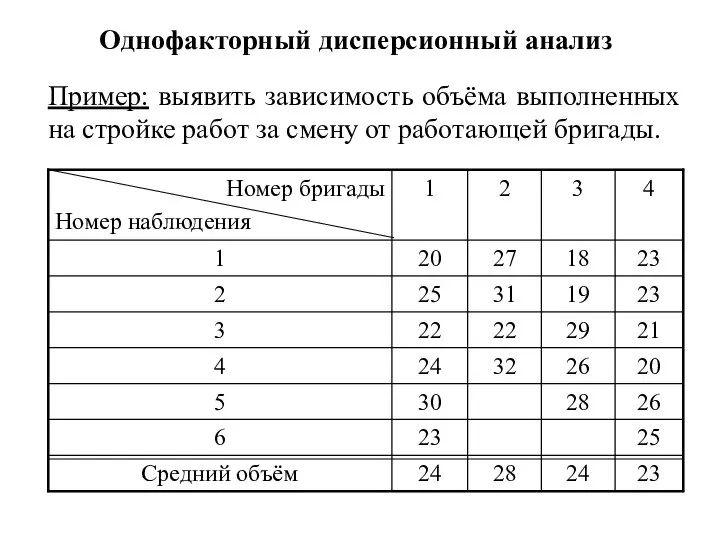
- 32. Однофакторный дисперсионный анализ Пример: выявить зависимость объёма выполненных на стройке работ за смену от работающей бригады.
- 33. X – случайная величина F – фактор, воздействующий на случайную величину X F1, F2, …, Fp
- 34. Критерий Бартлетта H0: D1(X) = D2(X) = … = Dp(X) гипотеза о равенстве дисперсий на каждом
- 35. Критерий: Если q1, q2, …, qp > 3, то критерий имеет распределение, близкое к распределению Пирсона
- 36. H0: a1 = a2 = … = ap Объём выборки: n = q1+ q2+…+ qp
- 37. 1-ая группа – уровень F1: x11, x21, … , 2-ая группа – уровень F2: x21, x22,
- 38. 1-ая группа – уровень F1: x11, x21, … , 2-ая группа – уровень F2: x21, x22,
- 39. i-тая группа: x1i, x2i, … , , групповая средняя: yi Diгр= Dвнгр= Остаточная сумма:
- 40. Факторная дисперсия: Остаточная дисперсия: – всегда – если несущественно влияние фактора H0: a1 = a2 =
- 41. Критерий: имеет распределение Фишера с (p–1) и (n–p) степенями свободы Критическая область W – правосторонняя: Из
- 42. Элементы теории корреляции Зависимость величины Y от X называется функцио-нальной, если каждому значению величины X соот-ветствует
- 43. Среднее значение, которое принимает величина Y при X=x, называется математическим ожиданием случай-ной величины Y, вычисленным при
- 44. f (x)=М(Y|X=x) – ? это уравнение называется выборочным уравнением регрессии, а функция f*(x) – выборочной функцией
- 45. Если функция регрессии – линейная: f (x) = М(Y|X=x) = ax+b, то выборочное уравнение регрессии имеет
- 47. Скачать презентацию









































 ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ»
ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ» Решение задач
Решение задач Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс)
Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс) В мире плоскостей
В мире плоскостей Решение задач. 6 класс
Решение задач. 6 класс Треугольник и его элементы
Треугольник и его элементы Игра Верю - не верю
Игра Верю - не верю Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Математическое путешествие в мир гармонии. Устный журнал
Математическое путешествие в мир гармонии. Устный журнал Живая планета!
Живая планета! Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Числовые промежутки
Числовые промежутки Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Распределение случайных величин. Функция распределения и плотность распределения случайной величины
Распределение случайных величин. Функция распределения и плотность распределения случайной величины Осевая и центральная симметрия
Осевая и центральная симметрия Радианная Мера Угла
Радианная Мера Угла Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани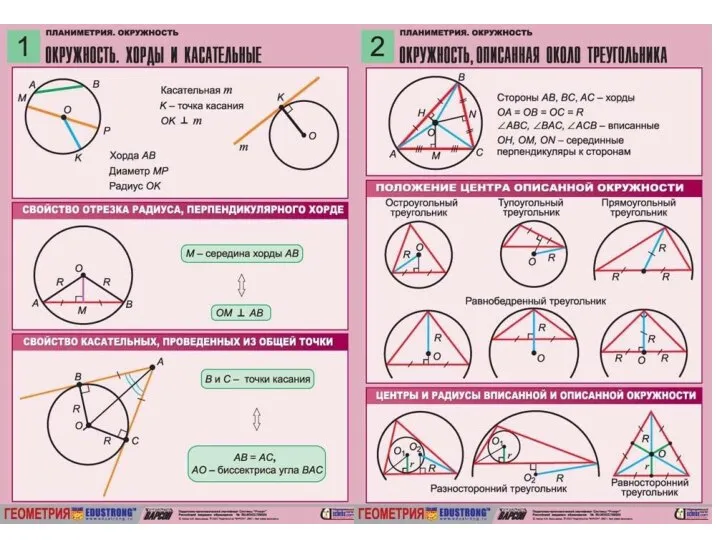 Геометрия. Конспекты
Геометрия. Конспекты Интегральное исчисление. Первообразная функция. Неопределённый интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Теория погрешностей
Теория погрешностей Треугольники. Решение задач
Треугольники. Решение задач Определение неизвестного числа
Определение неизвестного числа Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Станция логическая. По тропинкам занимательной математики
Станция логическая. По тропинкам занимательной математики Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики