Математика и музыка

Оглавление
Основные понятия
Древнегреческие ученные, изучавшие математику и музыку
Законы Пифагора – Архита
Интервалы
Пифагоров строй
Интервальные коэффициенты
Другие лады
Проблема переходов из одного лада в другой
Алгебра гармонии – темперация
Изменение пропорций в новой системе
Музыкальные творения в новой музыкально-математической системе
Заключение

Основные понятия
Гамма или звукоряд - Последовательный ряд звуков, повышающийся или понижающийся в пределах одной или нескольких октав.
Лад в музыке – это система отношений устойчивых и неустойчивых звуков и созвучий, которая работает на определённый звуковой эффект.
К оглавлению

Древнегреческие ученные, изучавшие математику и музыку
Архит Тарентский
К оглавлению
Пифагор Самосский

Законы Пифагора - Архита
К оглавлению
Высота тона звучащей струны обратно пропорциональна ее длине
Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4. Эти интервалы - "совершенные консонансы"

Интервалы
К оглавлению

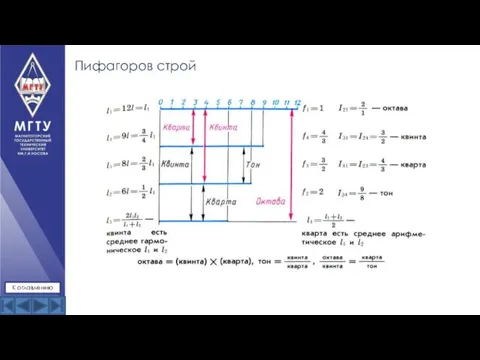
Пифагоров строй
К оглавлению

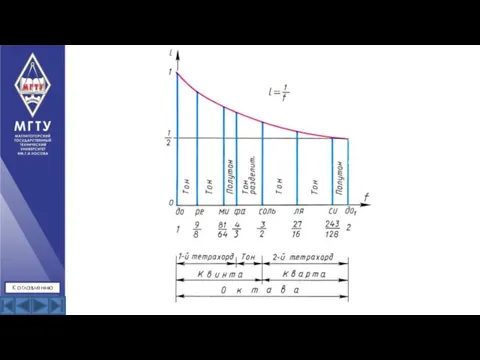
К оглавлению

Интервальные коэффициенты
К оглавлению

Другие лады
К оглавлению

Проблема переходов из одного лада в другой
К оглавлению
Так как расстояния между соседними ступенями пифагорова строя неодинаковы, Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад

Алгебра гармонии - темперация
К оглавлению
XVIII век в истории музыки начался решительной победой рационализма века Просвещения над антично-средневековым музыкальным целомудрием. К 1700 г. немецкий органист Андреас Веркмейстер (1645-1706) осуществил смелое и гениально простое решение: он отказался от совершенных и несовершенных консонансов - квинт, кварт и терций, оставив в первозданной консонантной красе лишь одну октаву, и попросту разделил ее геометрически на 12 равных частей. В результате пифагорова комма, которую до того времени нетронутой передвигали с места на место, также разделилась на 12 равных частей и стала незаметной. Так в музыке восторжествовала темперация (лат. соразмерность), а новый строй был назван равномерно-темперированным. Но по порядку...

Изменение пропорций в новой системе
К оглавлению

Музыкальные творения в новой музыкально-математической системе
К оглавлению
Бах написал свое бессмертное произведение "Хорошо темперированный клавир"