Решение уравнений математической физики методом д’Аламбера

16.24 Найти решение уравнения:
удовлетворяющее начальным условиям:

План решения:
Определяем тип уравнения.
Исходя из начальных условий и формулы Д’Аламбера,
определяем функции ϕ(x) и ψ(x).
Получаем решение уравнения u(x,t).
Строим графики прямой и обратной волн, а также их
суммарного воздействия для различных моментов времени t.

Решение
2. Уравнение Д’Аламбера имеет следующий вид:
1. Приведем уравнение к следующему виду:
где a=1, b=0, c=-1
- уравнение гиперболического типа
Т.е. мы имеем задачу Коши для однородного
(поскольку отсутствует внешняя среда) волнового уравнения.

Определим функции ϕ(x) и ψ(x).
=>
Воспользуемся указанной ранее формулой Д’Аламбера,
подставив в нее заданные функции (учтем, что а = 1):

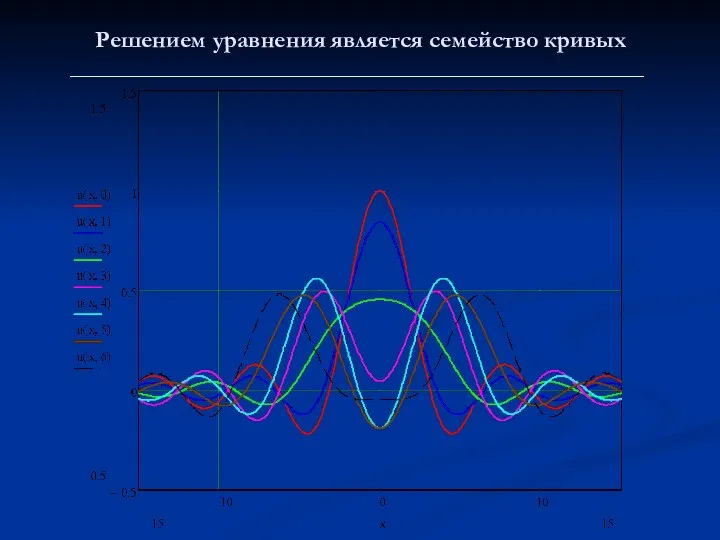
Решением уравнения является семейство кривых

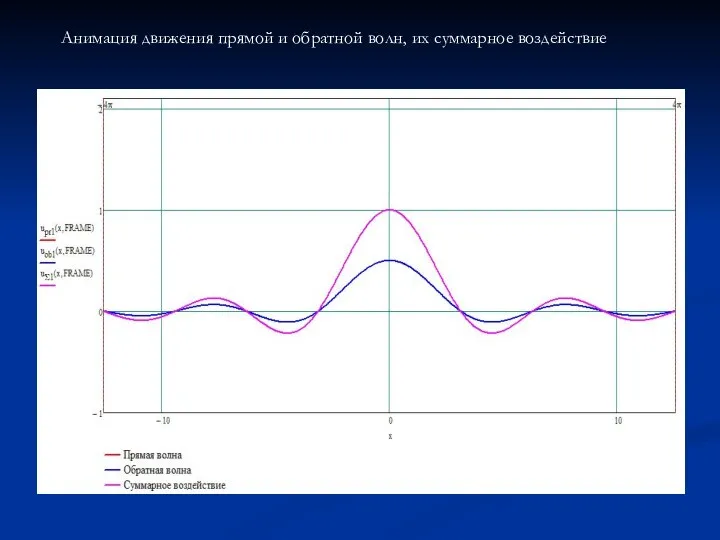
Анимация движения прямой и обратной волн, их суммарное воздействие

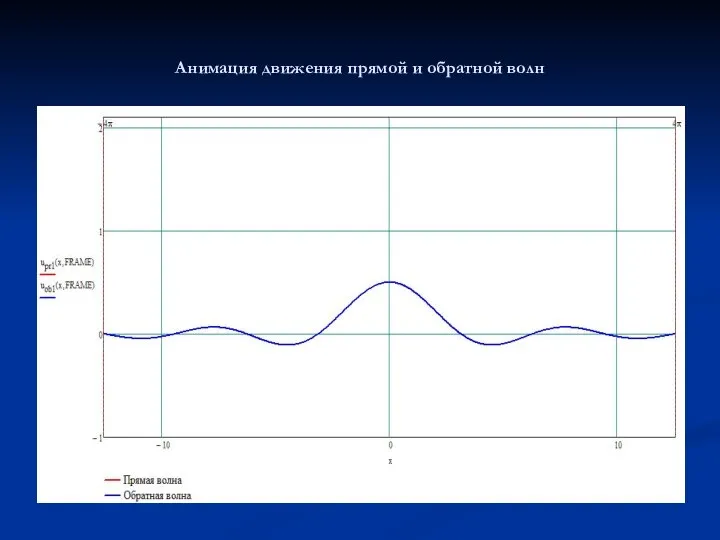
Анимация движения прямой и обратной волн