Слайд 2Если на величины Xi (i=1,…,n) наложено r связей, то число степеней свободы

k=n-r.
Плотность этого распределения определяе-тся: 0≤χ2<∞,
где -
гамма-функция (интеграл Эйлера второго рода). В частности Г(n+1)=n!.
Слайд 3Из определения плотности вероятности распределения χ2 следует, что распределение “хи-квадрат” определяется одним

параметром – числом степеней свободы k. С увеличением числа степеней свободы распределение “хи-квадрат” медленно приближается к нормальному.
Слайд 4При k=n>30 χ2 – распределение достаточно хорошо представляется нормальным законом с M[χ2]=n
![При k=n>30 χ2 – распределение достаточно хорошо представляется нормальным законом с M[χ2]=n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-3.jpg)
и D[χ2]=n. На рисунке показано, как изменяется характер распределения χ2 при увеличении числа степеней свободы k.
Слайд 56.6. Распределение Стьюдента
Пусть случайные величины Z, X1, X2, …, Xn подчинены нормальному

закону распределения с нулевым средним и произвольной дисперсией. Пусть далее величина Z не зависит от Xi, i = 1, …, n, и среди Xi имеется ровно k линейно независимых величин.
Слайд 6 Тогда случайная величина
имеет распределение Стьюдента (t-распределение), с плотностью распределения

Слайд 8Заметим, что t-распределение не зависит от σ2. Величина t, определенная для нормированных

случайных величин с нулевым средним и единичной дисперсией, также распределена по закону Стьюдента.
Распределение Стьюдента симметрично относительно начала координат. С возрастанием числа степеней свободы быстро приближается к нормальному закону распределения.
Слайд 9Для нормированных СВ распределения Стьюдента приближается к нормальному закону с характеристиками M[t]
![Для нормированных СВ распределения Стьюдента приближается к нормальному закону с характеристиками M[t]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-8.jpg)
= 0 и
D[t] = k / (k – 2).
Слайд 106.7. F-распределение Фишера
Если X и Y – независимые случайные величины, распределенные

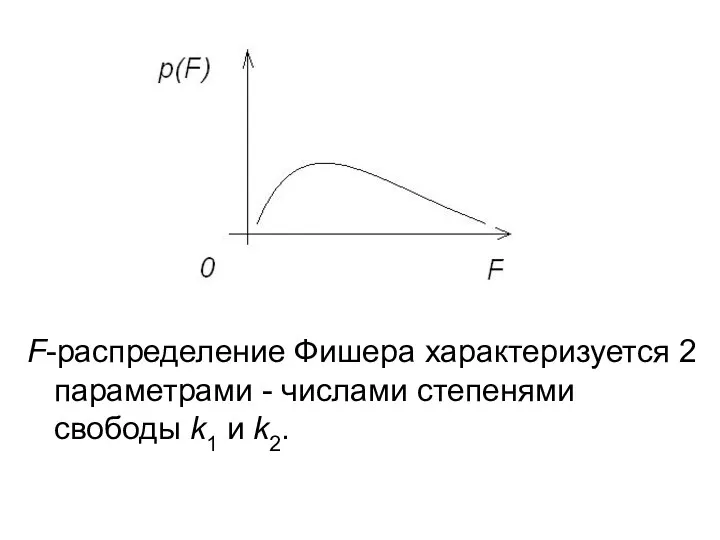
по закону χ2 со степенями свободы k1 и k2 , то величина имеет F- распределение Фишера со степенями свободы k1 и k2.
Слайд 11Плотность этого распределения определяется выражением

Слайд 12
F-распределение Фишера характеризуется 2 параметрами - числами степенями свободы k1 и k2.
Слайд 136.8. Первичная обработка результатов измерений
Первичная обработка результатов измерений состоит из последовательного выполнения

следующих шагов.
Слайд 141.Построение случайной выборки измерений и простого статистического ряда.
2.Построение вариационного ряда
3.Грубые ошибки измерений.

Исключение грубых ошибок.
4.Оценка математического ожидания случайной величины.
5.Оценка дисперсии случайной величины.
6.Оценка вероятности случайного события.
7.Оценка функции и плотности распределения случайной величины.
Слайд 15Рассмотрим более детально вопросы исключения грубых ошибок и оценки вероятности случайного события.
Получив

выборку наблюдений случайной величины Х с функцией распределения F(x) следует убедиться, что она действительно соответствует этой функции распределения.
Слайд 16 Так как в процессе измерений предполагаемая статистическая обстановка может нарушиться и

среди реализаций xi могут появляться ошибочные, т.е. не соответствующие F(x) значения.
Обычно в качестве ошибочных подразумевают xmin и xmax и их называют грубыми ошибками, если установлено их несоответствие закону F(x).
Слайд 17Если F(x) известно, то вопрос об ошибоч-ности xmax может быть решен следующим

образом. Зная F(x), можно найти
F(n)(x) – функцию распределения
X(n) = Xmax.
Тогда задаваясь вероятностью β≅1 практически достоверного события,
из уравнения
можно найти границу tβ, правее которой
Слайд 18появление реализации xmax в соответствии с принципом практической уверенности невозможно.
Отсюда следует

решающее правило: если xmax ≥ tβ, то xmax считают грубой ошибкой, в противном случае xmax считают согласующейся с законом распределения F(x).
В случае независимых измерений
Слайд 19Аналогично решается вопрос об ошибочности xmin . Здесь определяется граница tα из

условия:
где α=1-β - вероятность практически невозможного события.
Затем применяют решающее правило принципа практической уверенности:
Слайд 20xmin – грубая ошибка, если xmin < tα ; xmin не противоречит

F(x) – в противном случае.
При независимых измерениях tα находится из уравнения:
Чаще F(x) бывает неизвестной. Тогда для решения поставленной задачи применяют частные приемы.
Слайд 21Например, если F(x) нормального закона распределения с неизвестными параметрами m = M[X]
![Например, если F(x) нормального закона распределения с неизвестными параметрами m = M[X]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-20.jpg)
и σ2 = D[X], то строят вспомогательную случайную величину
где – оценка
среднеквадратического отклонения
Слайд 22Затем устанавливают ее функцию распределения FT(t) = P(T < t) далее находят

верхнюю границу tβ допустимых значений Т из уравнения FT(tβ) = β = 1 – α.
Верхней границей допустимых значений xmax становится величина
Слайд 23В итоге получаем следующее частное решающее правило: если
то она считается соответствующей нормальному

распределению;
в противном случае величина xmax считается грубой ошибкой.
Слайд 24Анализ ошибочности xmin выполняется аналогично по решающему правилу:
то xmin считается соответствующей нормальному

закону; в противном случае величину xmin считают грубой ошибкой.
Для определения границ tβ составлены специальные таблицы, входом которых служат n и α=1-β.
Слайд 25Оценим вероятность Р(А)=р появления события А в n опытах.
В качестве оценки

рассмотрим частоту событий:
p* = m*/n,
где m* - число опытов, в которых наблюдалось событие А,
n – общее число опытов.
Слайд 26Из т.Бернулли следует, что оценка вероятности события р* является состоятельной, является оценкой

сходящейся по вероятности к оцениваемому параметру.
Определим математическое ожидание и дисперсию оценки р*. Т.к. m* - случайная величина, распределенная по биномиальному закону с математическим ожиданием
M[m*] = np и дисперсией D[m*] = npq, то


![При k=n>30 χ2 – распределение достаточно хорошо представляется нормальным законом с M[χ2]=n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-3.jpg)


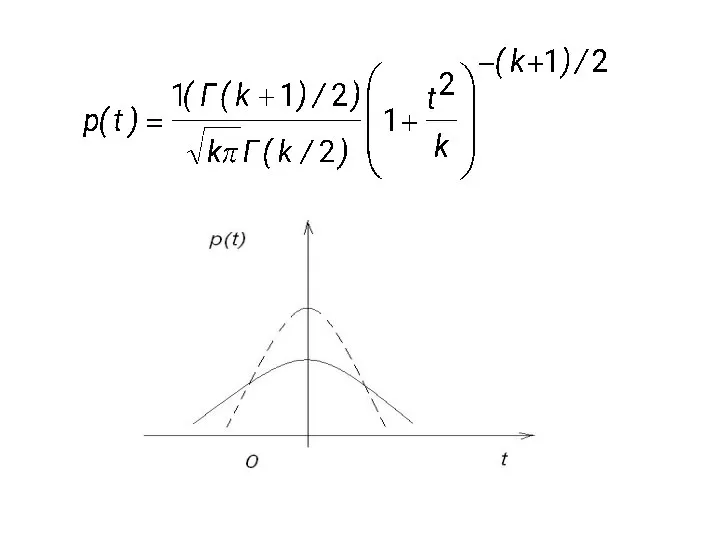

![Для нормированных СВ распределения Стьюдента приближается к нормальному закону с характеристиками M[t]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-8.jpg)











![Например, если F(x) нормального закона распределения с неизвестными параметрами m = M[X]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1134477/slide-20.jpg)





 История развития обыкновенных дробей
История развития обыкновенных дробей Свойства логарифмов
Свойства логарифмов Приёмы вычитания с переходом через десяток
Приёмы вычитания с переходом через десяток Счет в пределах 5
Счет в пределах 5 Сложение двузначных и однозначных чисел с переходом в другой разряд
Сложение двузначных и однозначных чисел с переходом в другой разряд Сравнение, сложение и вычитание обыкновенных дробей. 6 класс
Сравнение, сложение и вычитание обыкновенных дробей. 6 класс Геро́н Александри́йский
Геро́н Александри́йский Умножение числа на произведение
Умножение числа на произведение Определение расстояния по градусной сети
Определение расстояния по градусной сети Введение в аналитическую геометрию. Векторы на плоскости и в пространстве
Введение в аналитическую геометрию. Векторы на плоскости и в пространстве Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Теорема Безу (теорема об остатке и разложение на множители)
Теорема Безу (теорема об остатке и разложение на множители) Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Теорема косинусов
Теорема косинусов Равнобедренный треугольник. Окружность
Равнобедренный треугольник. Окружность Круговая окружность
Круговая окружность Презентация на тему Угол поворота. Радианная мера угла
Презентация на тему Угол поворота. Радианная мера угла  Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Планирование эксперимента. Логические основы
Планирование эксперимента. Логические основы Психогеометрия
Психогеометрия Презентация на тему Закон больших чисел. Теорема Чебышева
Презентация на тему Закон больших чисел. Теорема Чебышева  Умножение и деление десятичной дроби на 10, 100, 1000
Умножение и деление десятичной дроби на 10, 100, 1000 Таблицы истинности
Таблицы истинности Сложение векторов
Сложение векторов Построение таблиц истинности
Построение таблиц истинности Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Площадь трапеции
Площадь трапеции Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер