Пифагор и его египетский треугольник

ПИФАГОР
(др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570—490 гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.

В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»

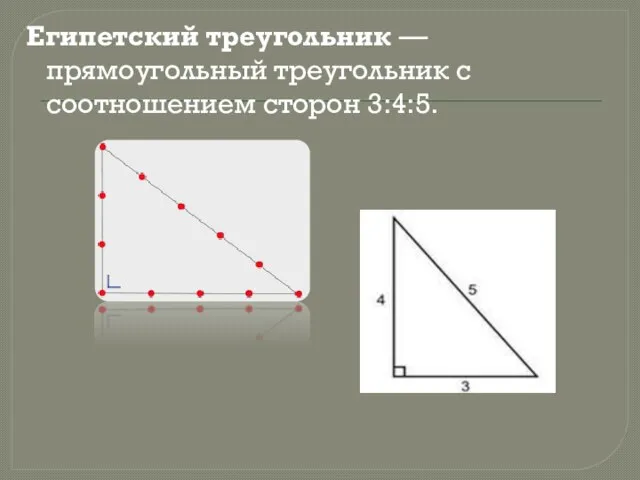
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

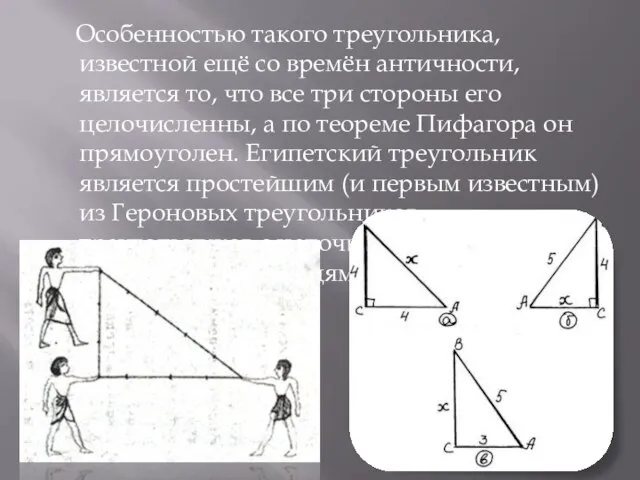
Особенностью такого треугольника, известной ещё со времён античности, является то, что все три стороны его целочисленны, а по теореме Пифагора он прямоуголен. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы

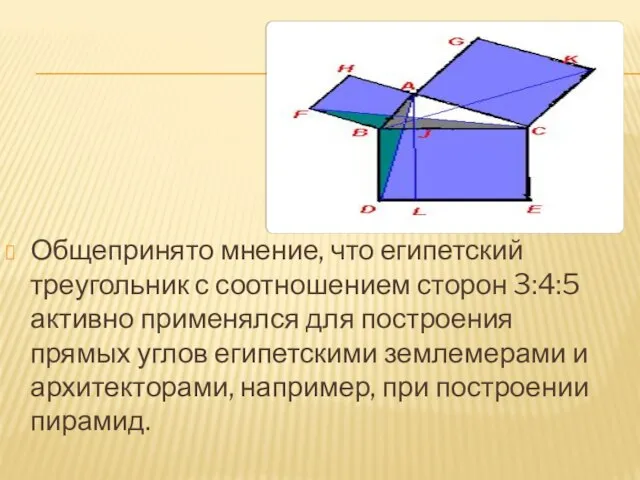
Общепринято мнение, что египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид.

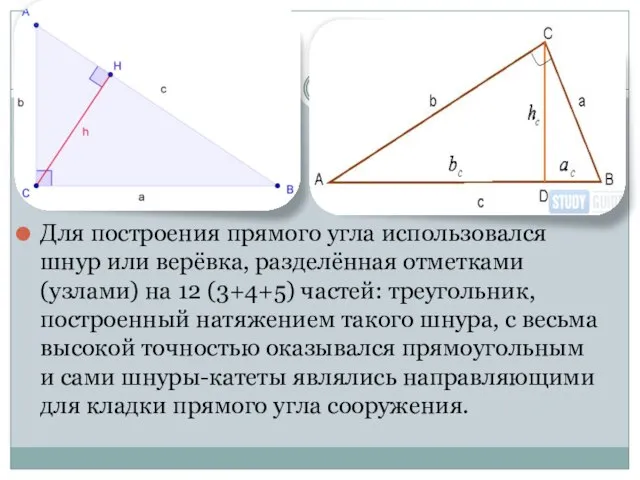
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.