Содержание
- 2. Свойства функций 1. Область определения D(f) 2. Область значений Е(f) 3. Нули функции 4. Промежутки знакопостоянства
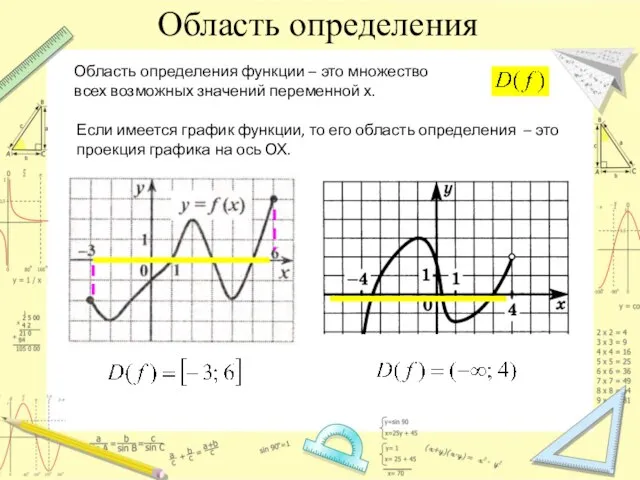
- 3. Область определения Область определения функции – это множество всех возможных значений переменной х. Если имеется график
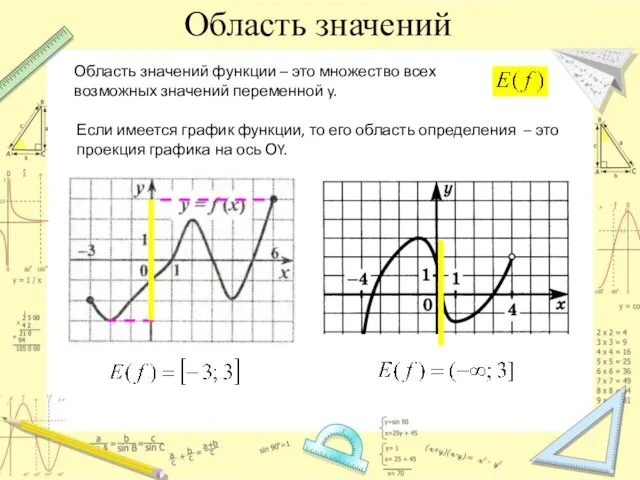
- 4. Область значений Область значений функции – это множество всех возможных значений переменной y. Если имеется график
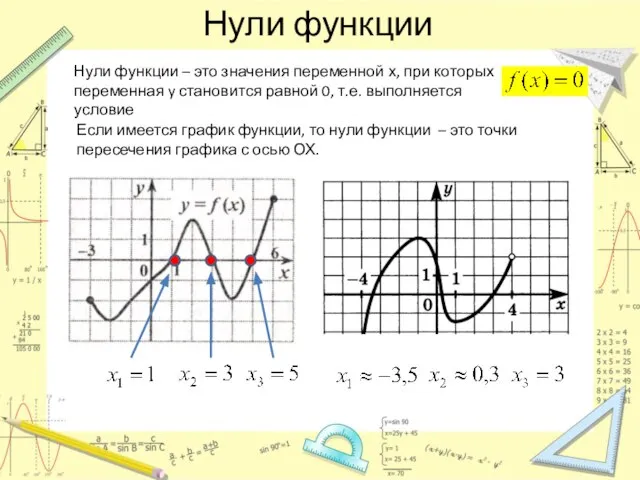
- 5. Нули функции Нули функции – это значения переменной х, при которых переменная y становится равной 0,
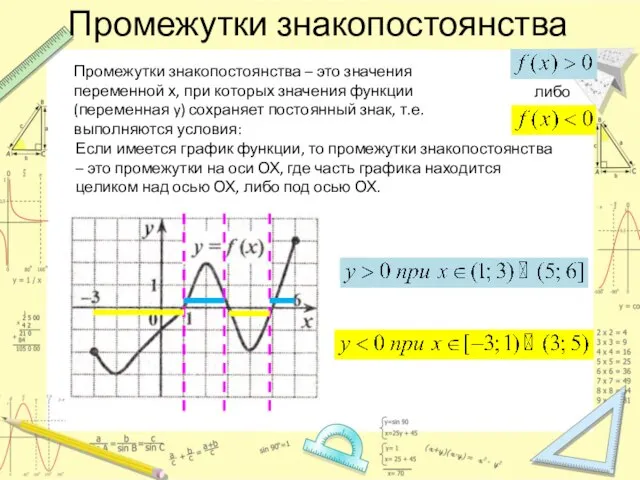
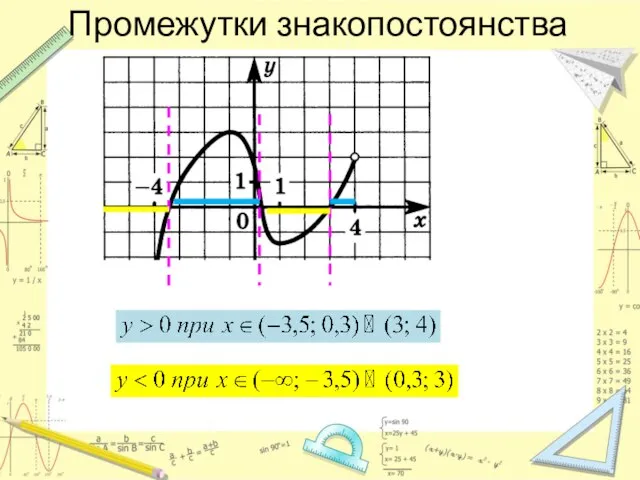
- 6. Промежутки знакопостоянства Промежутки знакопостоянства – это значения переменной х, при которых значения функции (переменная y) сохраняет
- 7. Промежутки знакопостоянства
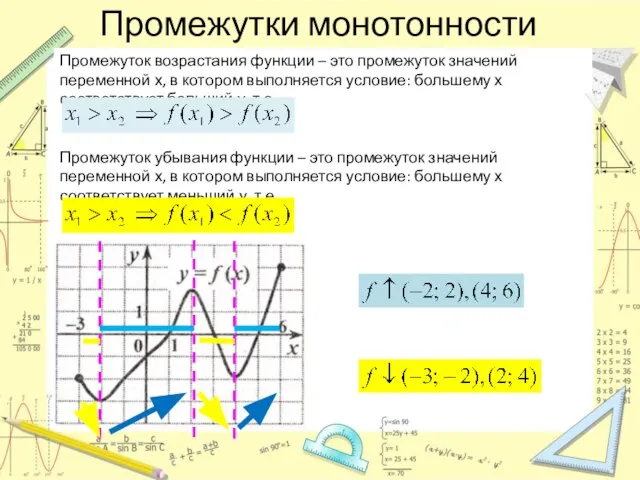
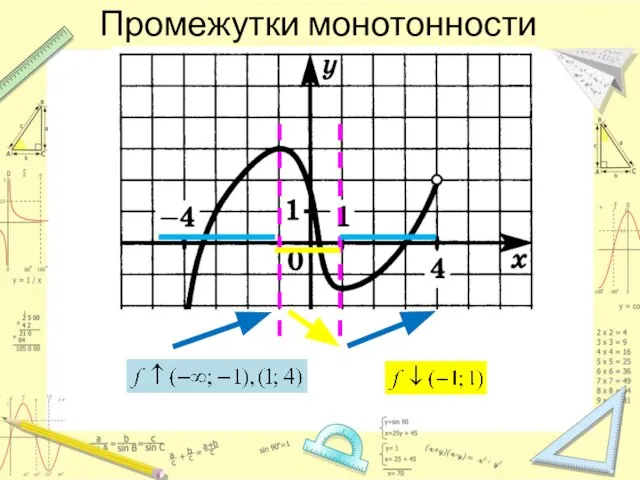
- 8. Промежутки монотонности Промежуток возрастания функции – это промежуток значений переменной х, в котором выполняется условие: большему
- 9. Промежутки монотонности
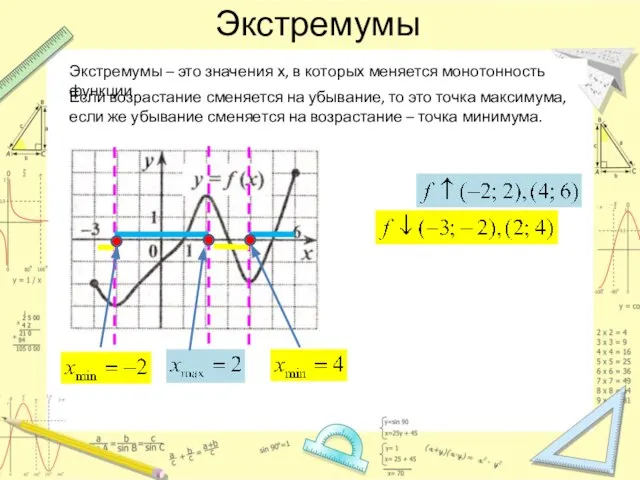
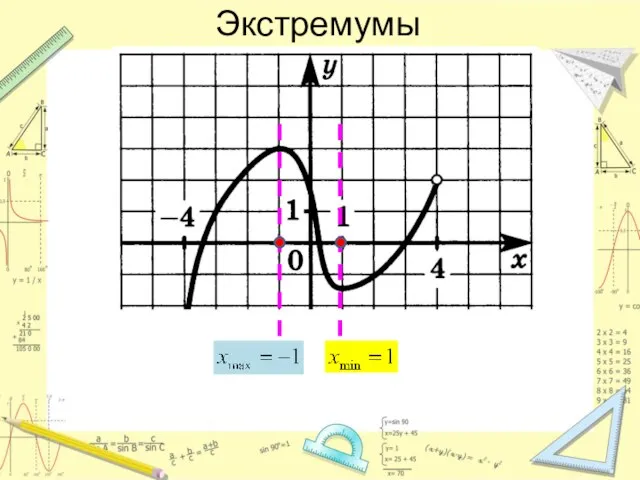
- 10. Экстремумы Экстремумы – это значения х, в которых меняется монотонность функции Если возрастание сменяется на убывание,
- 11. Экстремумы
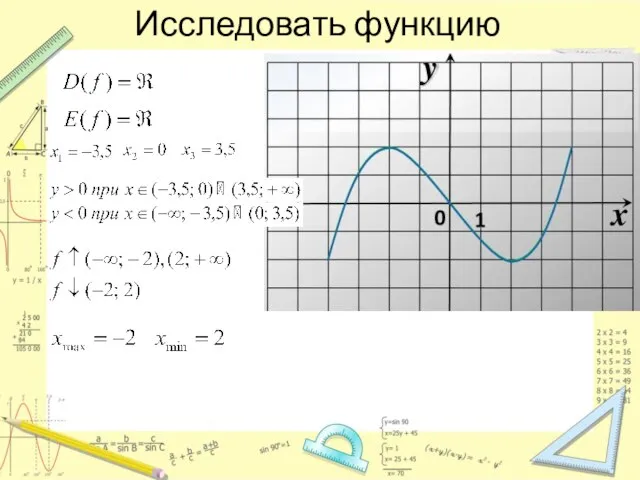
- 12. Исследовать функцию
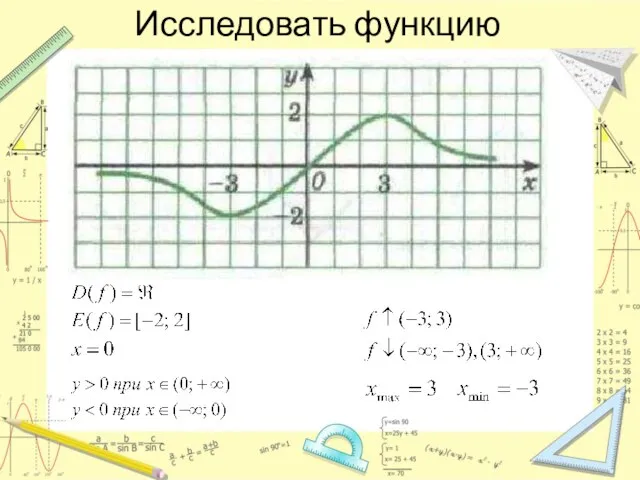
- 13. Исследовать функцию
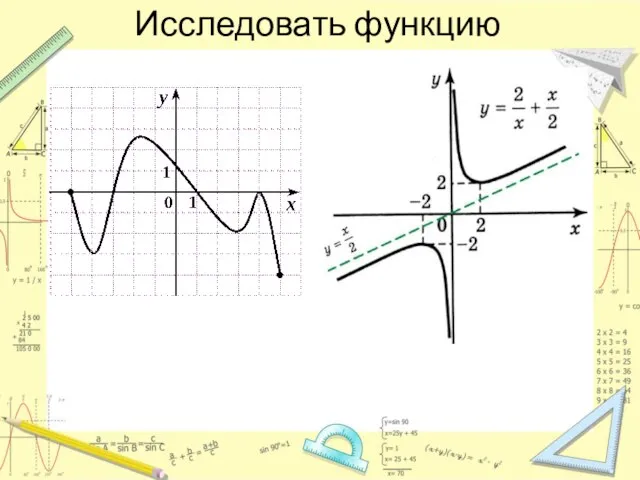
- 14. Исследовать функцию
- 16. Скачать презентацию

 Сравнение, сложение и вычитание обыкновенных дробей. 6 класс
Сравнение, сложение и вычитание обыкновенных дробей. 6 класс Прямоугольник
Прямоугольник Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Гиперболический параболоид
Гиперболический параболоид Деление дробей
Деление дробей Деление на 3
Деление на 3 Презентация на тему Объемы тел 11 класс
Презентация на тему Объемы тел 11 класс  Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Случаи сложения вида +5 с переходом через десяток
Случаи сложения вида +5 с переходом через десяток Показательные уравнения
Показательные уравнения Сто к одному
Сто к одному Квадратный корень
Квадратный корень Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»
Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»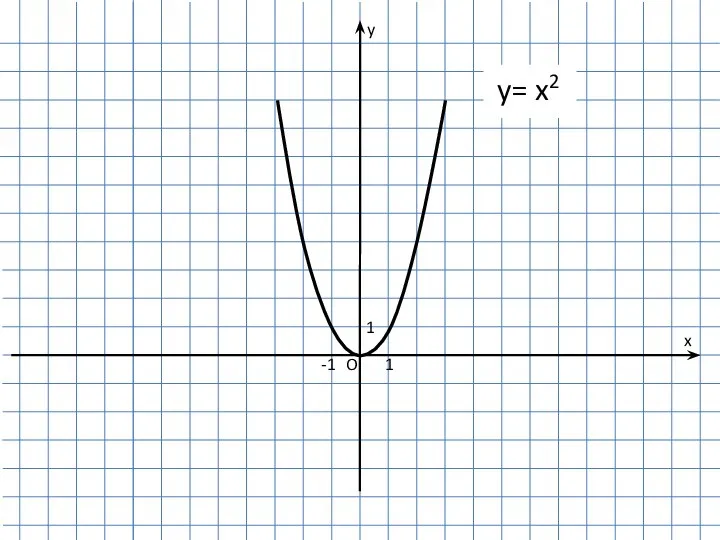 Преобразование графиков функции
Преобразование графиков функции Примеры на сложение и вычитание
Примеры на сложение и вычитание Задачи, обратные данной
Задачи, обратные данной Математическая эстафета
Математическая эстафета Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Презентация на тему Решение неравенств с одной переменной (11 класс)
Презентация на тему Решение неравенств с одной переменной (11 класс)  Квадратичная функция
Квадратичная функция Части задачи
Части задачи Классическое определение вероятности
Классическое определение вероятности Формулы. Урок 1
Формулы. Урок 1 Определители матриц
Определители матриц Построение сечений многогранников
Построение сечений многогранников Счёт
Счёт Введение в геометрию
Введение в геометрию Задачи математической карусели. 4 класс
Задачи математической карусели. 4 класс