Метод наименьших квадратов оценки параметров функциональной зависимости

Что такое МНК?
Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Почему МНК?

Общий вид модели
Модель в общем виде может быть представлена уравнением:
yt = a0 + a1 х1t +...+ an хnt + εt .
Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1 , y2 , ... , yT )' и матрица значений независимых переменных
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .

Применение
Метод наименьших квадратов используется для оценки параметров уравнение регрессии.
Регрессионный анализ представляет собой вывод уравнения регрессии, с помощью которого находится средняя величина случайной переменной (признака-результата), если величина другой (или других) переменных (признаков-факторов) известна. Он включает следующие этапы:
выбор формы связи (вида аналитического уравнения регрессии);
оценку параметров уравнения;
оценку качества аналитического уравнения регрессии.

Пример использования
X– торговую площадь продовольственного магазина, кв.м.,
Y – годовой товарооборот продовольственного магазина, млн. руб.
Предположим, что после проведения наблюдений/опытов/подсчётов в нашем распоряжении оказываются числовые данные:

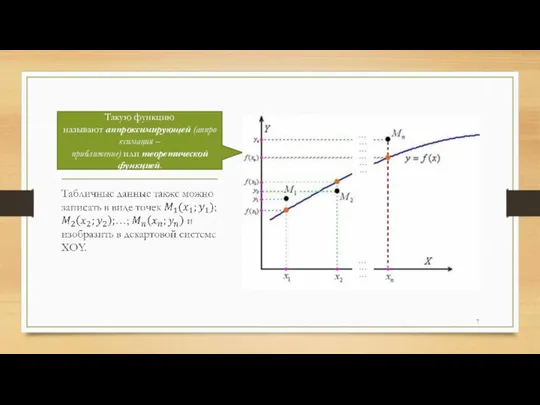
Такую функцию называют аппроксимирующей (аппроксимация – приближение) или теоретической функцией.

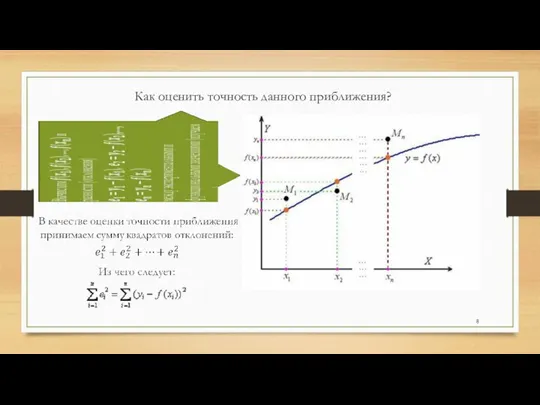
Как оценить точность данного приближения?

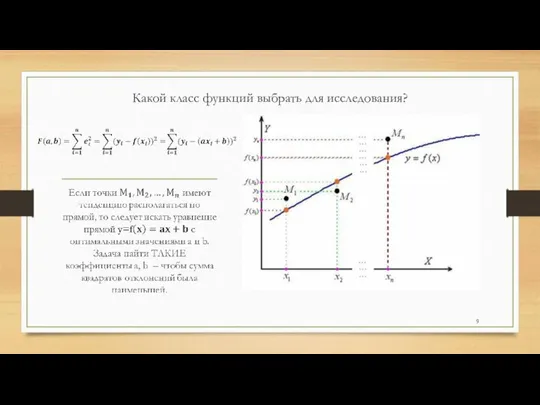
Какой класс функций выбрать для исследования?

Сначала найдем частные производные 1-го порядка.
Согласно правилу линейности дифференцировать можно прямо под значком суммы:

Составим стандартную систему:
Сокращаем каждое уравнение на «двойку» и, кроме того, «разваливаем» суммы:

Перепишем систему в «прикладном» виде:
После чего начинает прорисовываться алгоритм решения нашей задачи:
1) Составляем простейшую систему двух линейных уравнений с двумя неизвестными («а» и «бэ»). Систему решаем, в результате чего получаем стационарную точку
2) Проверяя достаточное условие экстремума, можно убедиться, что в данной точке функция достигает именно минимума.

Делаем окончательный вывод: