Стохастические процессы

Если бы заявки поступали регулярно, через точно определенные промежутки времени, и обслуживание каждой заявки тоже имело определенную длительность, расчет пропускной способности системы не представлял бы никакой сложности. На фондовом рынке моменты поступления заявок случайны, а также случайна и длительность выполнения этой заявки брокером. В связи с этим процесс работы системы протекает нерегулярно: заявки могут попадать в очередь или не приходить вовсе. Таким образом, процесс функционирования системы массового обслуживания представляет собой случайный процесс.

Стационарный пуассоновский поток

Стационарный пуассоновский поток

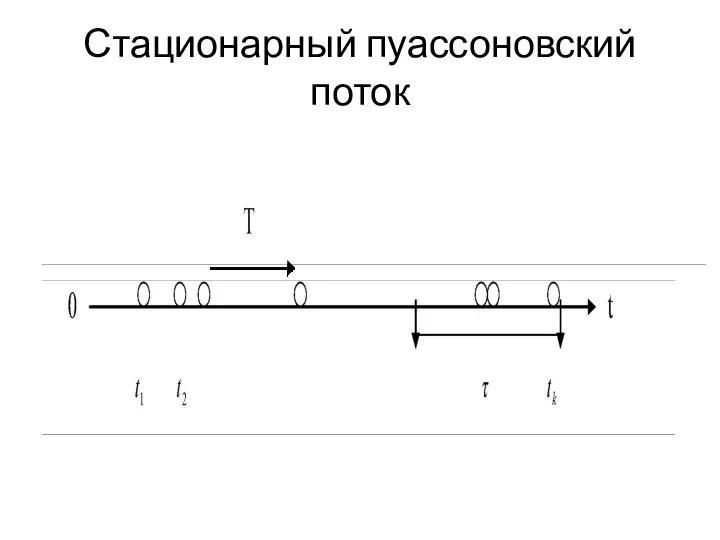
Если поток событий обладает всеми тремя свойствами (т. е. ста­ционарен, ординарен и не имеет последействия), то он называется простейшим (или стационарным пуассоновским) потоком. Название «пуассоновский» связано с тем, что при соблюдении условий 1 - 3 число событий, попадающих на любой фиксированный интервал вре­мени, будет распределено по закону Пуассона:
где λ - плотность потока (среднее число событий, приходящееся на единицу времени).

Марковский случайный процесс
Допущения о пуассоновском характере потока заявок и о показательном распределении времени обслуживания позволяют применить в теории массового обслуживания аппарат так называемых марковских случайных процессов. Процесс, протекающий в экономической системе, называется марковским (или процессом без последействия), если для каждого мо­мента времени вероятность любого состояния системы в бу­дущем зависит только от состояния системы в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние.

Стохастический процесс - это процесс, описывающий измене­ния в одной или нескольких переменных, когда эти изменения ха­рактеризуются неопределенностью. В особенности эти процессы применимы к анализу будущих изменений цен фондовых активов, так как эти изменения действительно неопределенны на эффективном рынке. Теория случайных процессов является одним из наиболее мощных и широко используемых инструментов анализа финансовых рынков. Слу­чайные процессы, как правило, являются наиболее адекватной моделью, описывающей динамику экономических переменных фондового рынка.

Согласно современной финансовой теории, известной как гипотеза эффективных рынков (efficient market hypothesis, ЕМН), цены ак­тивов отображают всю историческую информацию, касающуюся этого актива, и немедленную реакцию на поступающую новую информацию по этому активу. Эта ответная реакция проявляется в виде изменения цены. Если рынки немедленно реагируют на новую информацию и каждая часть новой инфор­мации независима от предыдущей, то изменения в ценах активов будут следовать марковскому процессу.

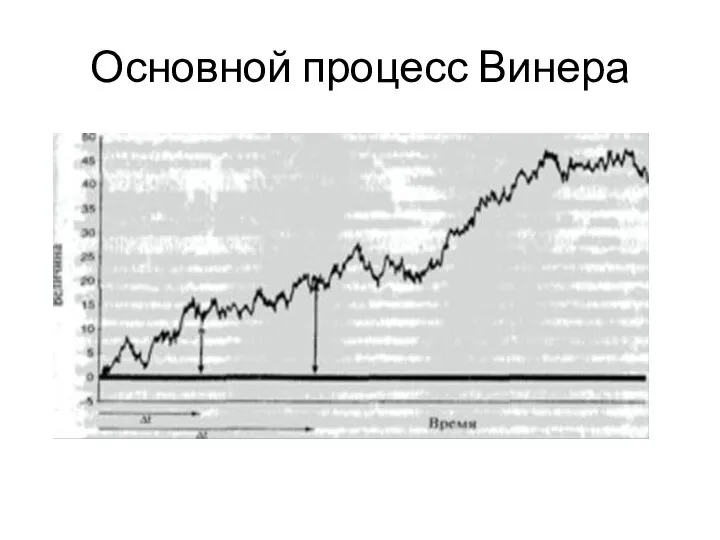
Процесс Винера или броуновское движение
Разновидность марковского процесса, которая используется как отправная точка для определения стохастических процессов цен активов, это основной процесс Винера (basic Wiener process), или броуновское движение (Brownian motion), названный в честь Норберта Винера, впервые сформулировавшего строгую математическую теорию для данного вида случайных процессов. В данном случае на исследуемую переменную воздействует большое количество случайных независимых импульсов или воздействий со стороны других переменных. Опишем процесс движения цен ак­тивов, который можно представить как результат сово­купного эффекта влияния многих независимых случайных импульсов, являющихся следствием получения новой информации.

Основной процесс Винера

Основной процесс Винера

Основной процесс Винера

Обобщенный процесс Винера

Процесс Ито