Множества и операции над ними

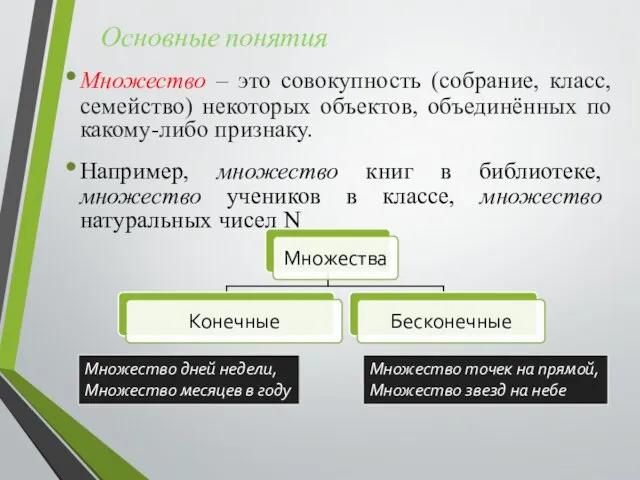
Множество – это совокупность (собрание, класс, семейство) некоторых объектов, объединённых по какому-либо признаку.
Например, множество книг в библиотеке, множество учеников в классе, множество натуральных чисел N
Множество точек на прямой,
Множество звезд на небе
Множество дней недели,
Множество месяцев в году
Основные понятия

Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.
Принадлежность предмета некоторому множеству обозначают с помощью символа ∈ (в противном случае используется символ ∉).
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c… z.
Например: А ={1, 3, 15}
Объекты, из которых образовано множество, называются элементами.
Если множество не содержит ни одного элемента, оно называется пустым и обозначается ∅

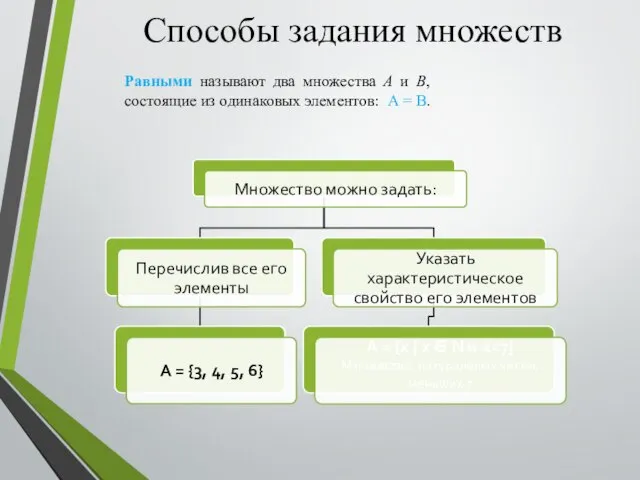
Способы задания множеств
Равными называют два множества A и B, состоящие из одинаковых элементов: А = В.

Множества удобно изображать с помощью кругов Эйлера.
Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В
И обозначают А ⊂ В.
Равными называют два множества A и B, состоящие из одинаковых элементов: А = В.

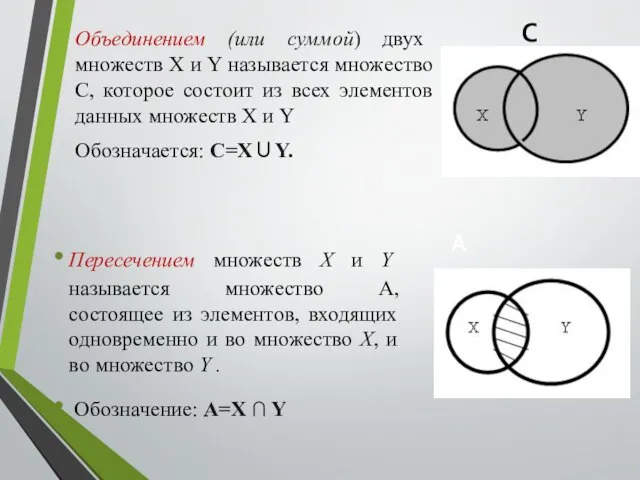
Объединением (или суммой) двух множеств X и Y называется множество С, которое состоит из всех элементов данных множеств X и Y
Обозначается: С=X∪Y.
C
Пересечением множеств Х и Y называется множество А, состоящее из элементов, входящих одновременно и во множество Х, и во множество Y .
Обозначение: А=X ∩ Y
A

Разностью множеств X и Y называется множество, содержащее все элементы множества X, не содержащиеся в Y.
Обозначение: X\Y

Алгебраические свойства
U - универсальное множество, т.е. все рассматриваемые объекты, являются его элементами.

Числовые множества
Введем обозначения для наиболее часто используемых множеств:
Множество R содержит рациональные и иррациональные числа

Теорема: Не существует рационального числа, квадрат которого равен числу 2
Свойства множества R действительных чисел