Содержание
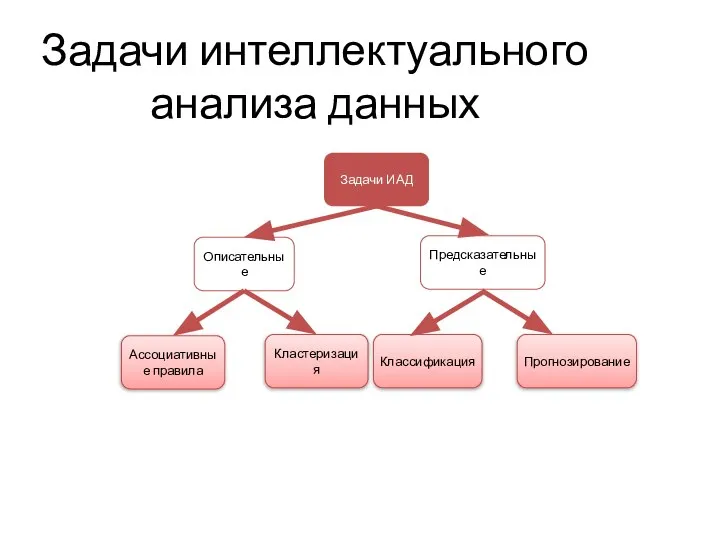
- 2. Задачи интеллектуального анализа данных Задачи ИАД Описательные Ассоциативные правила Кластеризация Классификация Прогнозирование Предсказательные
- 3. Введение Задача кластеризации состоит в разделении исследуемого множества объектов на группы «похожих» объектов, называемых кластерами Решение
- 4. Кластеризация отличается от классификации тем, что этап обучения на примерах отсутствует В задачах классификации множество классов
- 5. Задача кластеризации часто решается на начальных этапах исследования, когда о данных мало что известно Ее решение
- 6. ПРИМЕР –кластеризация результатов поиска
- 8. Формальная постановка задачи Дано множество данных, состоящее из N объектов (векторов): S1, S2, …, SN Каждый
- 9. Формальная постановка задачи Таким образом, i-й объект можно записать в виде: Si = (xi1, xi2, …,
- 10. Формальная постановка задачи Требуется: найти способ сравнения d(Sp, Sq) объектов между собой (меру сходства, функцию расстояния)
- 11. евклидово расстояние Манхэттенское расстояние расстояние Чебышева Метрики расстояния между объектами
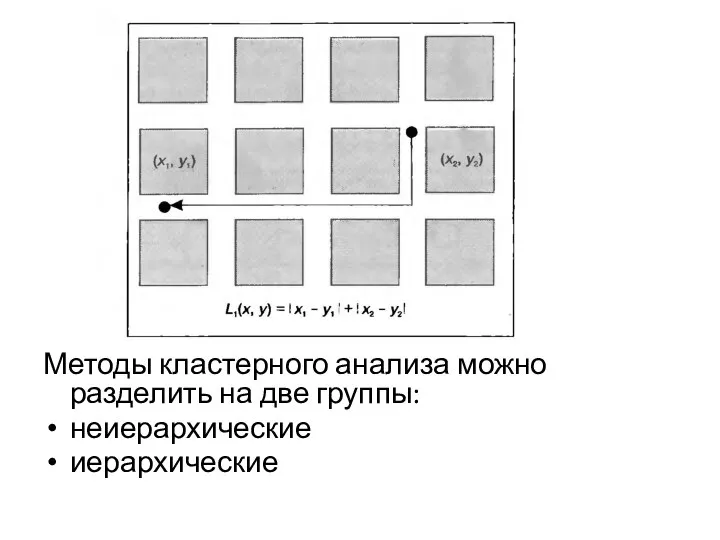
- 12. Методы кластерного анализа можно разделить на две группы: неиерархические иерархические
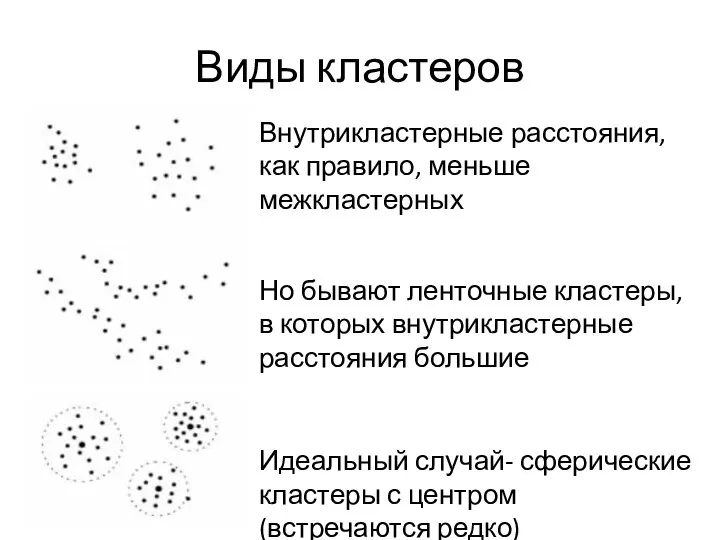
- 13. Виды кластеров Внутрикластерные расстояния, как правило, меньше межкластерных Но бывают ленточные кластеры, в которых внутрикластерные расстояния
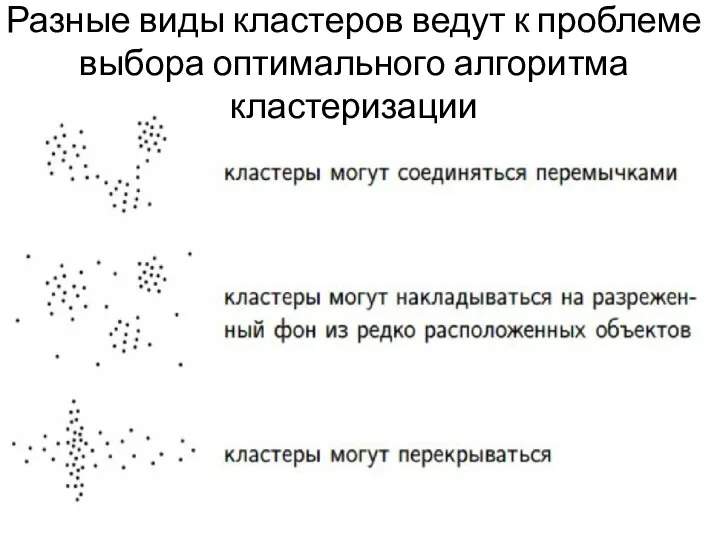
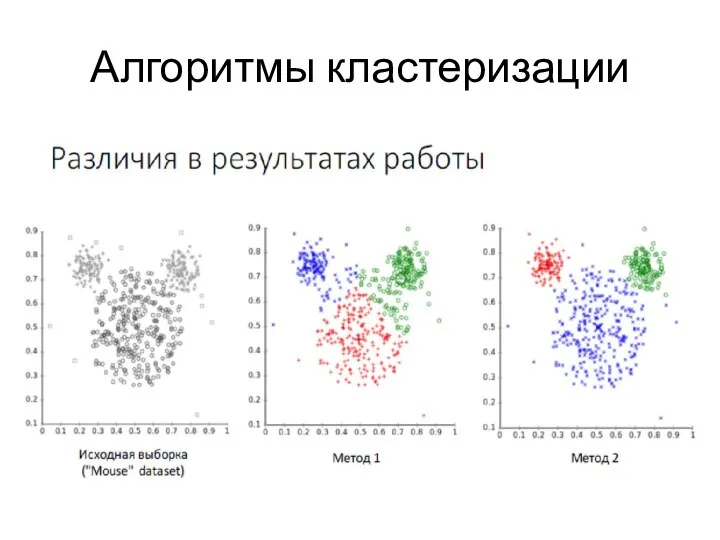
- 14. Разные виды кластеров ведут к проблеме выбора оптимального алгоритма кластеризации
- 15. Алгоритмы кластеризации
- 16. Как сделать признаки равноправными в образовании кластеров? ИТОГ: мы получим значения признаков, 95% которых находится в
- 17. Метод k-средних Неиерархическим методом кластеризации является метод k-средних (k-means) Предварительно необходимо выбрать вероятное число кластеров k
- 18. Метод k-средних 1. Выбирается k произвольных исходных центров кластеров – обычно выбираются k объектов 2. Все
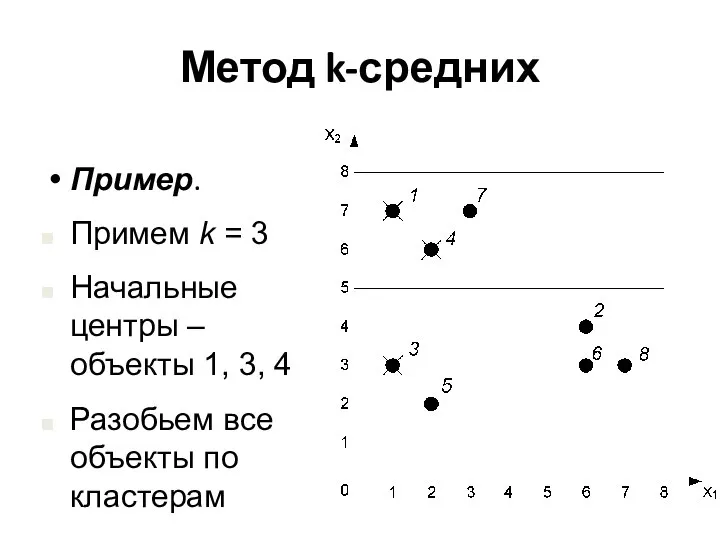
- 19. Метод k-средних Пример. Примем k = 3 Начальные центры – объекты 1, 3, 4 Разобьем все
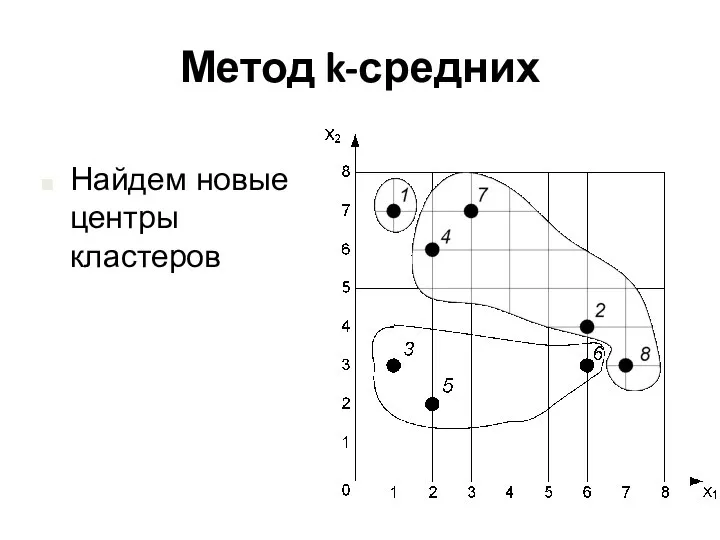
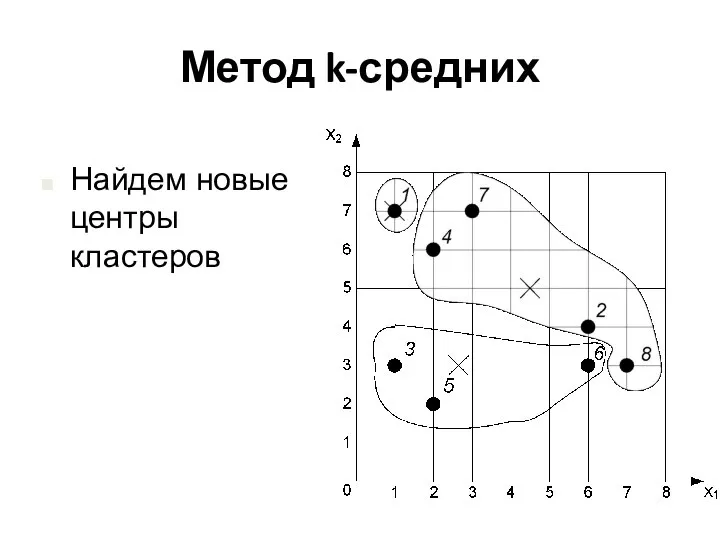
- 20. Метод k-средних Найдем новые центры кластеров
- 21. Метод k-средних Найдем новые центры кластеров
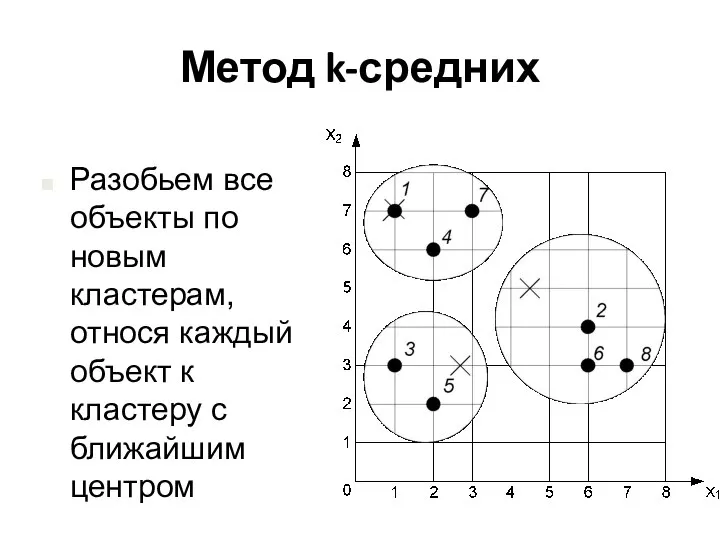
- 22. Метод k-средних Разобьем все объекты по новым кластерам, относя каждый объект к кластеру с ближайшим центром
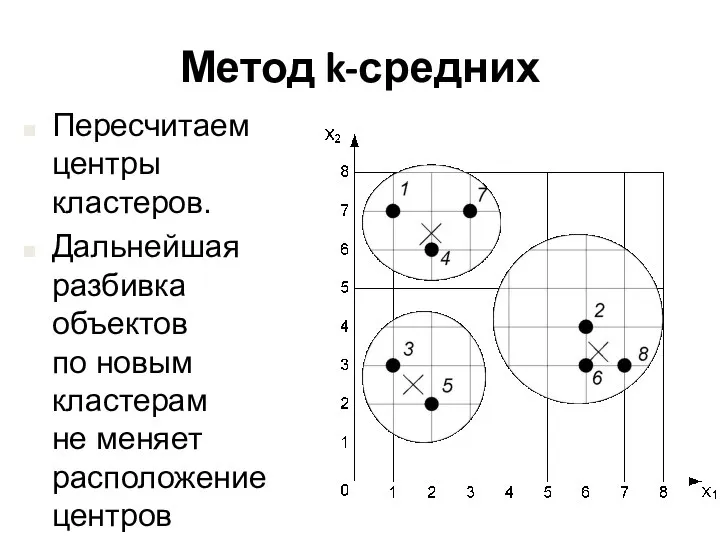
- 23. Метод k-средних Пересчитаем центры кластеров. Дальнейшая разбивка объектов по новым кластерам не меняет расположение центров
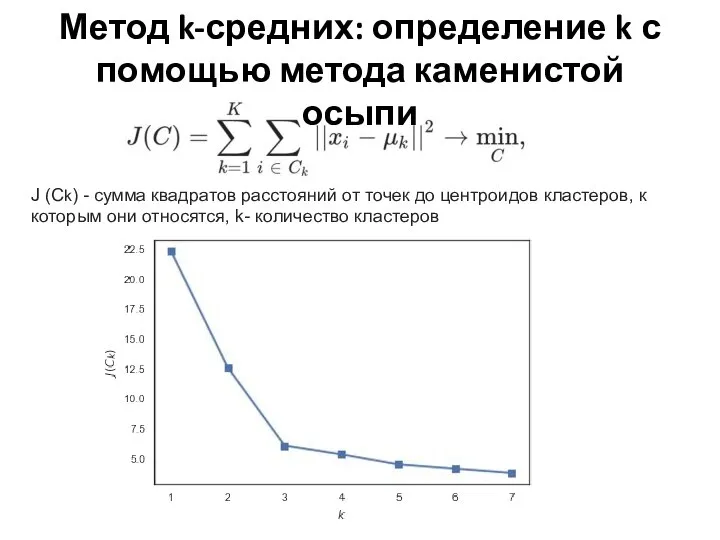
- 24. Метод k-средних: определение k с помощью метода каменистой осыпи J (Ck) - сумма квадратов расстояний от
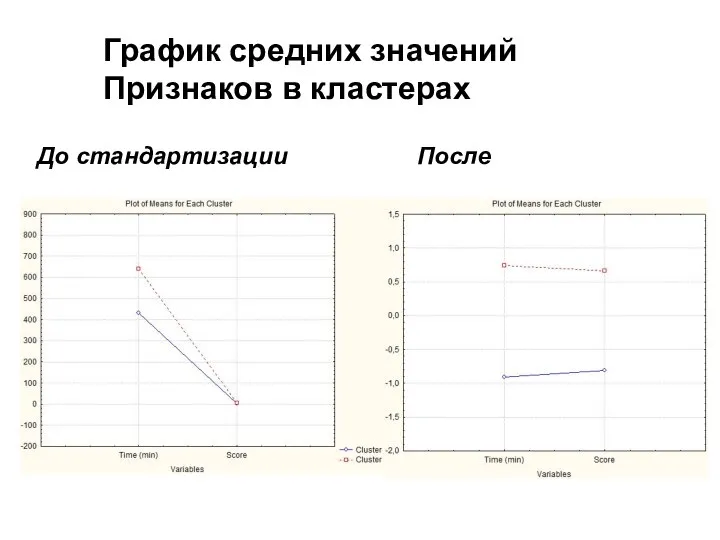
- 25. До стандартизации После График средних значений Признаков в кластерах
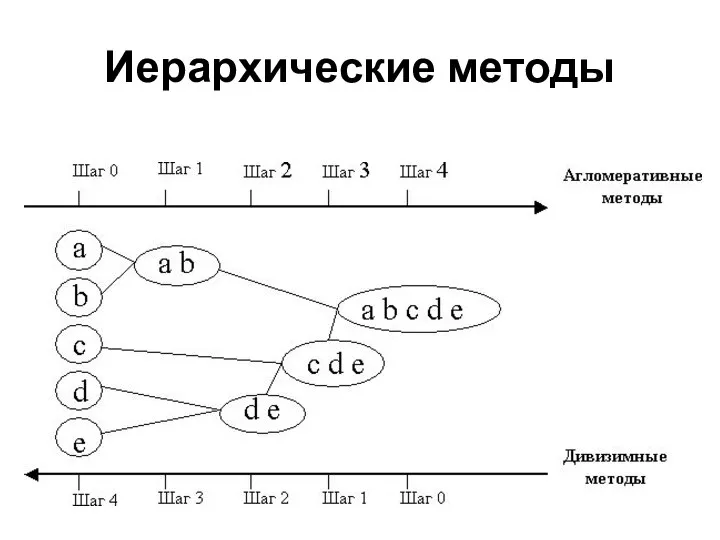
- 26. Иерархические методы К иерархическим методам кластеризации относятся: агломеративный алгоритмы дивизимный алгоритмы
- 27. Агломеративный метод В начале работы алгоритма все объекты являются отдельными кластерами На первом шаге наиболее похожие
- 28. Метод ближайшего соседа (одиночная связь, Single linkage). Расстояние между двумя кластерами определяется расстоянием между двумя наиболее
- 29. 4. Невзвешенный центроидный метод (Unweighted pair-group centroid). В этом методе расстояние между двумя кластерами определяется как
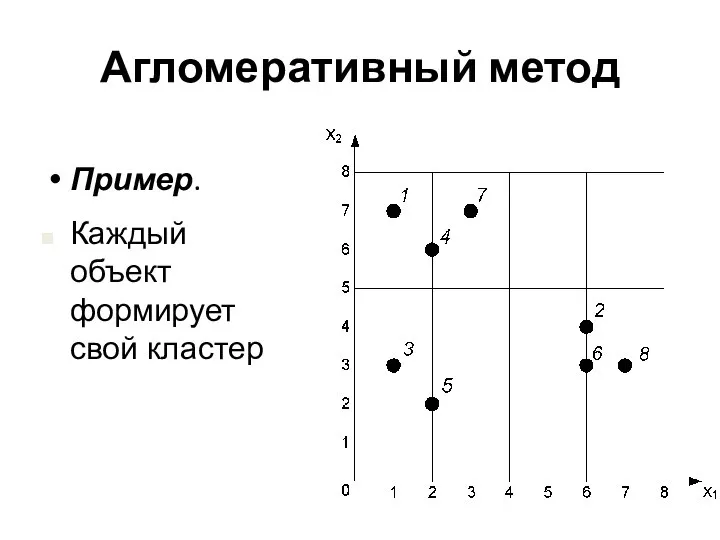
- 30. Агломеративный метод Пример. Каждый объект формирует свой кластер
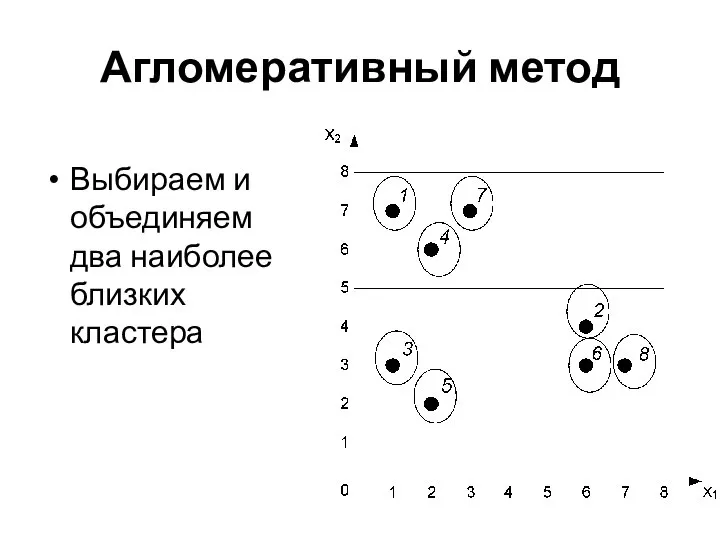
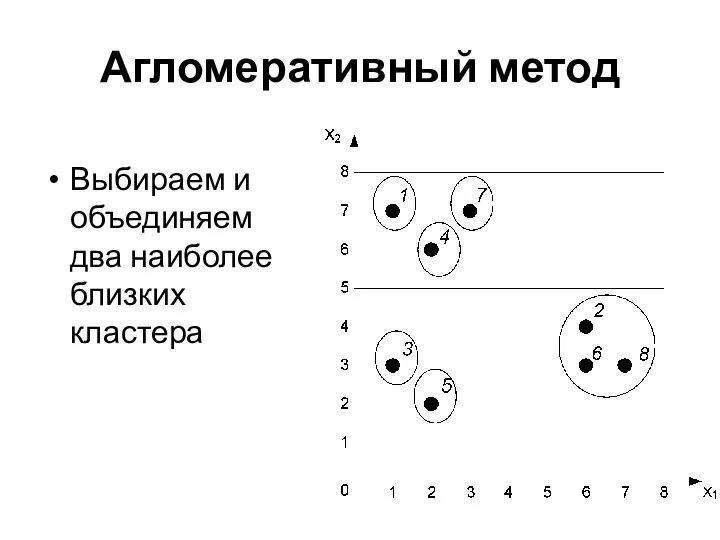
- 31. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
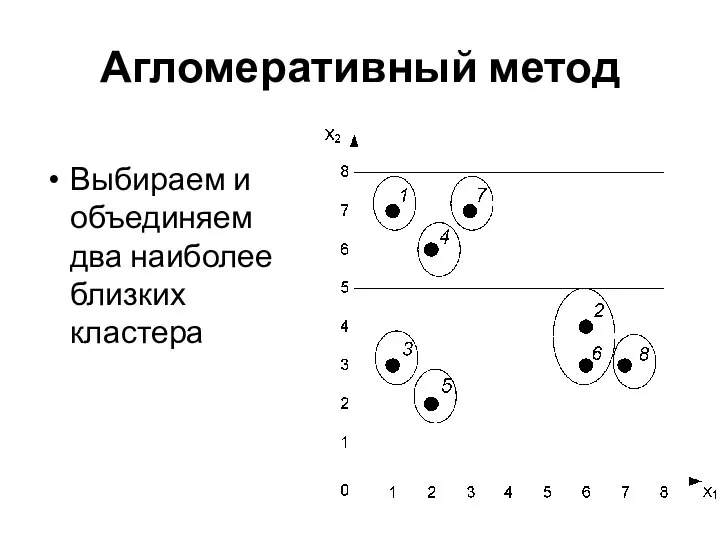
- 32. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
- 33. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
- 34. Дивизимный метод На первом шаге все объекты помещаются в один кластер С1 Выбирается объект, у которого
- 35. Дивизимный метод Выбранный объект удаляется из кластера С1 и формирует первый элемент второго кластера С2 На
- 36. Дивизимный метод В результате один кластер делится на два дочерних, один из которых расщепляется на следующем
- 37. Иерархические методы
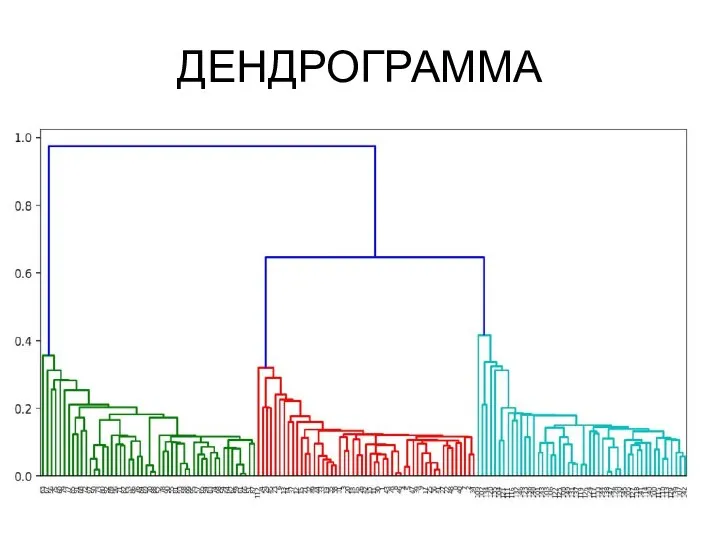
- 38. ДЕНДРОГРАММА
- 39. Метрики качества кластеризации Коэффициент силуэта: Здесь a — среднее внутрикластерное расстояние (то есть среднее расстояние между
- 40. Пример программы на Python from sklearn import datasets dataset = datasets.load_iris() X = dataset.data y =
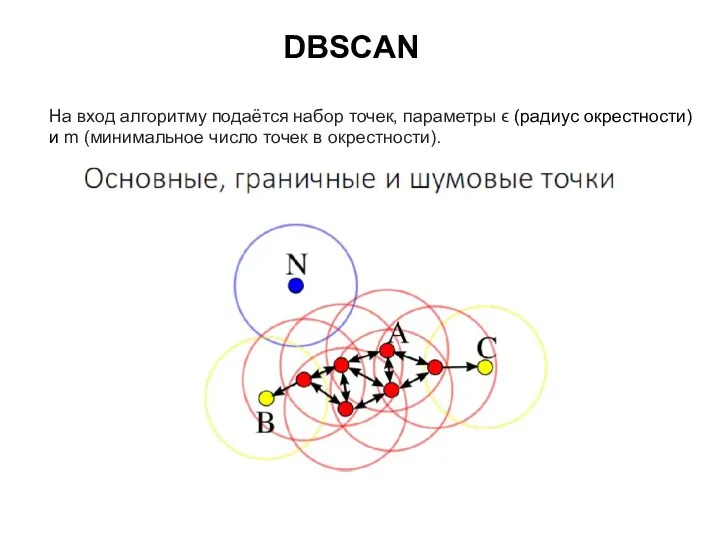
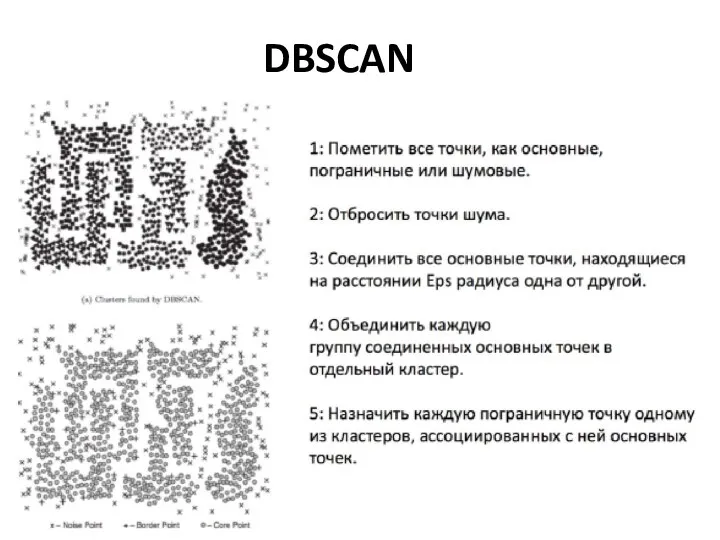
- 41. DBSCAN На вход алгоритму подаётся набор точек, параметры ϵ (радиус окрестности) и m (минимальное число точек
- 42. DBSCAN
- 43. DBSCAN: результаты работы
- 45. Скачать презентацию









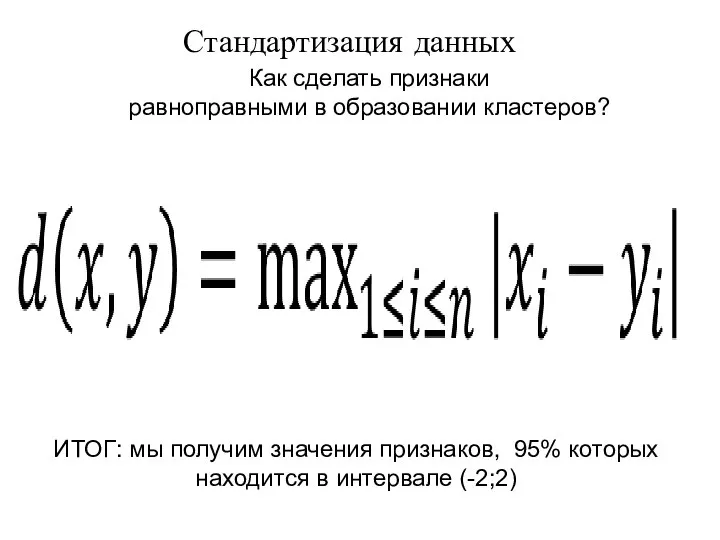












 2_Teoria_veroyatnostey_920_is
2_Teoria_veroyatnostey_920_is Среднее арифметическое
Среднее арифметическое Методы прогнозирования потерь в осевых турбинах
Методы прогнозирования потерь в осевых турбинах Сложение +5
Сложение +5 Решение иррациональных уравнений
Решение иррациональных уравнений Наклонный круговой цилиндр
Наклонный круговой цилиндр Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Определенный интеграл
Определенный интеграл Таблица умножение на двух значное число
Таблица умножение на двух значное число Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение
Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение Презентация на тему Деятельностный подход в обучении на уроках математики
Презентация на тему Деятельностный подход в обучении на уроках математики  Что такое проекция вектора
Что такое проекция вектора Диофантовы уравнения
Диофантовы уравнения Игра по станциям математический турнир. 7 класс
Игра по станциям математический турнир. 7 класс Электронные методические материалы на тему: Золотое сечение для учащихся 5-6 классов
Электронные методические материалы на тему: Золотое сечение для учащихся 5-6 классов Решение задач
Решение задач Применение интеграла к решению практических задач
Применение интеграла к решению практических задач Геометрические фигуры. 1 класс
Геометрические фигуры. 1 класс Куб. Теорема Эйлера
Куб. Теорема Эйлера Презентация на тему Полупрямая
Презентация на тему Полупрямая  Возникновение первых математических понятий
Возникновение первых математических понятий Тела вращения. Цилиндр и его элементы
Тела вращения. Цилиндр и его элементы Решение задачи с использованием циклов
Решение задачи с использованием циклов Статистическая обработка измерений
Статистическая обработка измерений Умножение на 1 и 0
Умножение на 1 и 0 Выполните деление
Выполните деление Формулы тангенсов и котангенсов
Формулы тангенсов и котангенсов Теория вероятности.Операции над событиями
Теория вероятности.Операции над событиями