Числа - близнецы

История
Первую таблицу простых чисел составил Эратосфен и предложил интересный метод нахождения простых чисел на интервале [2, n] ("решето Эратосфена").

Эратосфен
(276-194г.г. до н.э.)

Эратосфен заметил, что многие простые числа группируются в пары близнецов: таковы 11 и 13, 29 и 31, 41 и 43.
Теория простых чисел богата древнейшими нерешенными проблемами.
Последовательность простых чисел подчиняется какой-то плохо различимой закономерности, и простые числа живут по собственным правилам. Их сравнивают с сорной травой, случайным образом распределенной среди натуральных чисел.
Перебирая одно за другим натуральные числа, можно набрести на области, богатые простыми числами, но, по неизвестной причине, другие области оказываются
совершенно пустыми.
С чего началось изучение чисел-близнецов

Математики веками пытались разгадать закон, по которому распределены простые числа, и всякий раз терпели поражение.
Возможно, никакого закона не существует, и распределение простых чисел случайно по самой своей природе.
Например, две тысячи лет назад Евклид доказал, что запас простых чисел неисчерпаем.
Верно ли то же самое для чисел-близнецов? Эта задача не покорилась Эратосфену.

В наши дни "проблема близнецов" остается единственной не решенной задачей, которая досталась нам от Античности.
Последние два столетия математики пытались доказать, что запас простых чисел-близнецов также неисчерпаем.
Под числами–близнецами понимают пары простых чисел, отличающиеся на 2, и являющиеся ближайшими соседними простыми числами.
Существуют веские основания полагать, что множество простых чисел-близнецов бесконечно, но никому пока не удалось доказать, что это действительно так.

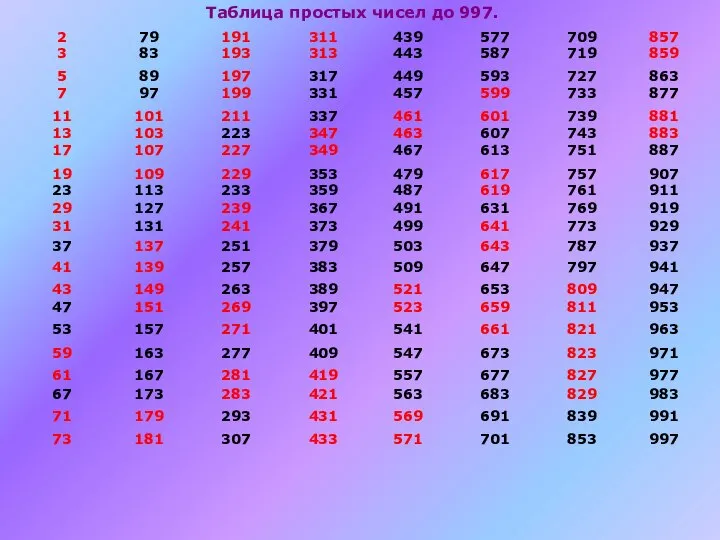
Таблица простых чисел до 997.

Среди простых чисел встречаются так называемые "близнецы" или пары простых чисел, разница между которыми составляет двойку (например, 11 и 13).
Именно эти пары чисел в таблице учебника выделены другим цветом.

"Близнецы" появляются с некой периодичностью, причем, чем больше числа, тем реже они встречаются (11 и 13; 17 и 19; 29 и 31; 41 и 43; 59 и 61).
То же происходит и с обычными простыми числами.
В числах, близких к триллиону, лишь каждое 28 число является простым.

Все пары простых чисел-близнецов, кроме (3, 5) имеют вид 6n 1
Действительно.
Рассмотрим пример:
17 и 19
17=6*3-1
19=6*3+1

Первые числа-близнецы:
(3; 5), (5; 7), (11; 13), (17; 19), (29; 31), (41; 43), (59; 61), (71; 73), (101; 103), (107; 109), (137; 139), (149; 151), (179; 181), (191; 193), (197; 199), (227; 229), (239; 241), (269; 271), (281; 283), (311; 313), (347; 349), (419; 421), (431; 433), (461; 463), (521; 523), (569; 571), (599; 601), (617; 619), (641; 643), (659; 661), (809; 811), (821; 823), (827; 829), (857; 859), (881; 883)…

Задания.
Найти пары “БЛИЗНЕЦОВ”(устно):
823
13
659
7
199
617
311
149
5
313
661
151
821
197
619
11
№ 1

Перед вами числа-близнецы? Нет - докажите.
14 и 16
2 и 3
3)347 и 349
4) 313 и 315
5)599 и 601
6)239 и 241
Ответ: 1) нет (4- составное число); 2) нет (не имеют вид 6х 1); 3) да; 4) нет (315 – составное число); 5) да; 6) да.
№ 2