Слайд 5Геометрический смысл производной
Значение производной f '(x0) равно угловому коэффициенту касательной, проведенной к

кривой
y = f '(x) в точке M0(x0, f(x0)): f '(x0) = kкас.
Уравнение касательной, проходящим через точку M0, имеет вид: y − y0 = f '(x0) (x − x0).
Нормаль – прямая, проходящая через точку касания перпендикулярно касательной. Тогда kнорм = − 1/kкас.
Уравнение нормали: y − y0 = (− 1/f '(x0))·(x − x0).
Слайд 6Пример. Составить уравнения нормали к линии
y = x3+ 3x2 − 5,

параллельной прямой 2х − 6у + 1 = 0.
Слайд 17§5. Исследование функции
Проводится по следующей схеме
1. Область определения функции D(f).
Множество значений

функции E(f).
2. Четность, нечетность, периодичность
f(х) – четная ⇔ ∀х, (−х)∈D(f) f(− х) = f(х)
(график симметричен относительно оси Оу)
f(х) – нечетная ⇔ ∀х, (−х)∈D(f) f(− х) = − f(х)
(график симметричен относительно начала координат)
Если ни одно условие не выполняется, то
f(х) – функция общего вида.
Слайд 18f(х) – периодическая с периодом Т ⇔
∀х, (х−Т), (х+Т) ∈D(f) f(х)

= f(х−Т) = f(х+Т)
(определяется только для тригонометрических функций)
3. Точки пересечения графика с осями координат
Пересечение с Оу существует, если х = 0 ∈D(f), точка пересечения (0, f(0))
(график пересекает Оу не более чем в одной точке).
Пересечение с Ох определяется в результате решения уравнения: f(х) = 0.
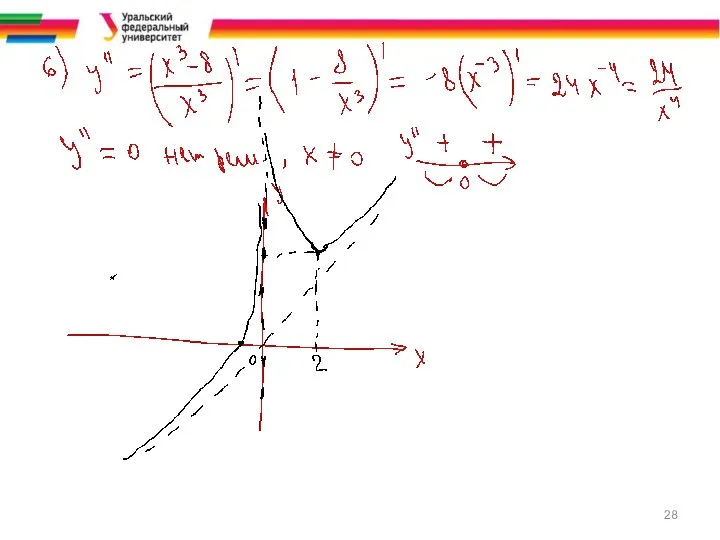
Слайд 24По результатам исследования строят график функции и при необходимости находят
7.* Дополнительные точки.


























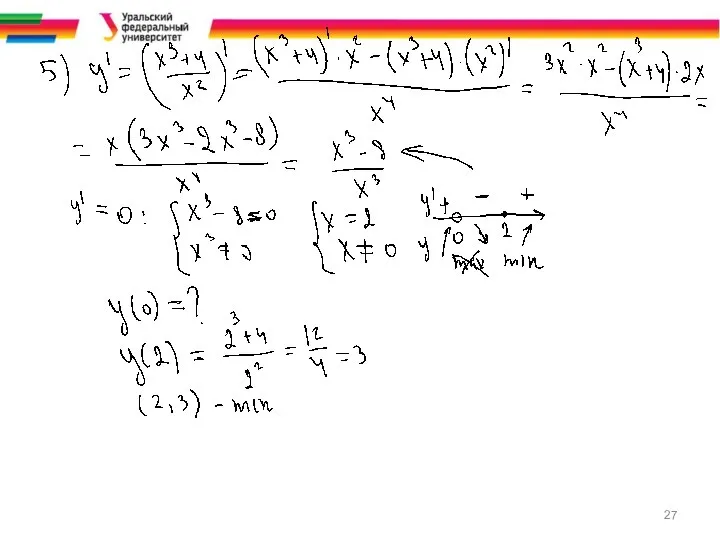




 Признаки параллельности прямых
Признаки параллельности прямых Задача с экологическим содержанием
Задача с экологическим содержанием Разные задачи. Способ Пропорция
Разные задачи. Способ Пропорция Иррациональные уравнения. Открытый урок
Иррациональные уравнения. Открытый урок Необычные способы вычислений
Необычные способы вычислений Путешествие в зазеркалье. Проект по геометрии
Путешествие в зазеркалье. Проект по геометрии Уходя, гасите свет. Математические расчеты
Уходя, гасите свет. Математические расчеты Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Конструирование из счётных палочек
Конструирование из счётных палочек Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые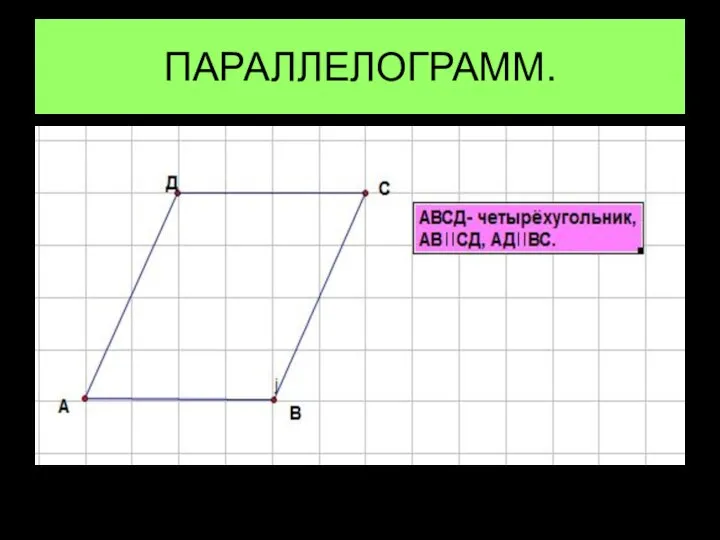 Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки В гостях у геометрических фигур
В гостях у геометрических фигур Сложение отрицательных чисел
Сложение отрицательных чисел Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс Решение задач по теме Правильные многоугольники
Решение задач по теме Правильные многоугольники Дидактические игры в детском саду
Дидактические игры в детском саду Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Бином Ньютона. Треугольник Паскаля. Решение задач
Бином Ньютона. Треугольник Паскаля. Решение задач Задуманное число. Общий множитель
Задуманное число. Общий множитель Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Конус. Цилиндр. Сфера
Конус. Цилиндр. Сфера Множество значений тригонометрических функций
Множество значений тригонометрических функций Квадратные неравенства
Квадратные неравенства Числа от 1 до 1000, умножение и деление. Приемы устных вычислений
Числа от 1 до 1000, умножение и деление. Приемы устных вычислений Плоскости
Плоскости Решение задач составлением систем уравнений с двумя переменными
Решение задач составлением систем уравнений с двумя переменными Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка