Перпендикуляр и наклонная

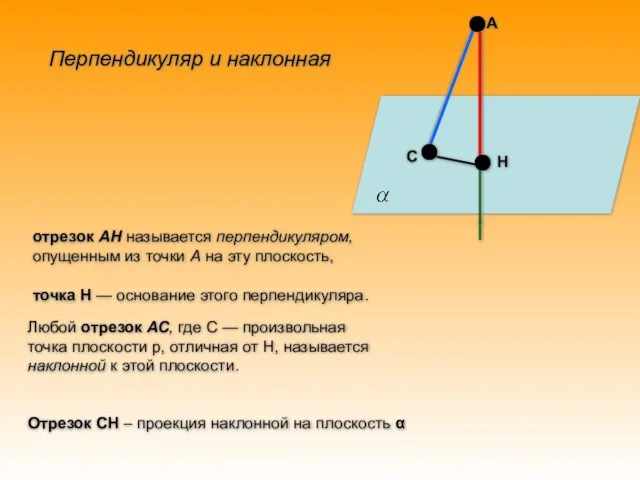
А
Н
С
отрезок АН называется перпендикуляром, опущенным из точки А на эту плоскость,
точка Н — основание этого перпендикуляра.
Любой отрезок АС, где С — произвольная точка плоскости p, отличная от Н, называется наклонной к этой плоскости.
Отрезок СН – проекция наклонной на плоскость α
Перпендикуляр и наклонная

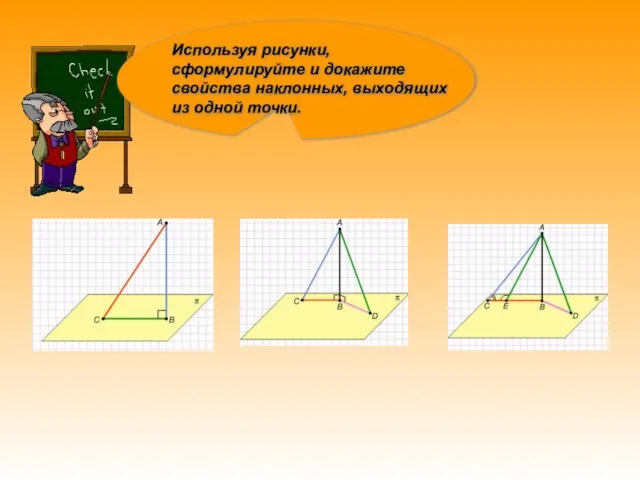
Используя рисунки, сформулируйте и докажите свойства наклонных, выходящих из одной точки.

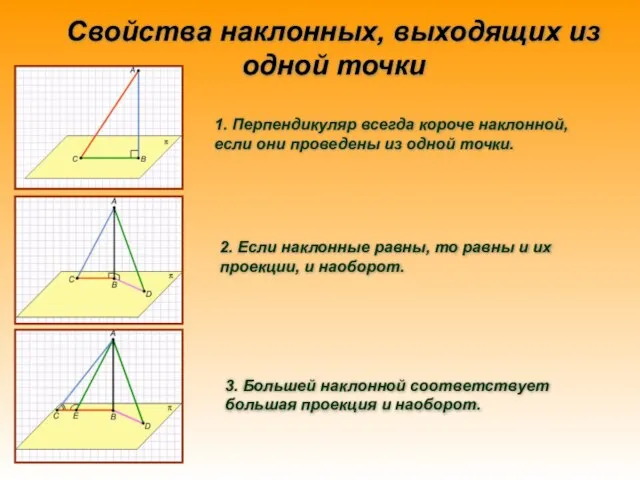
Свойства наклонных, выходящих из одной точки
1. Перпендикуляр всегда короче наклонной, если они проведены из одной точки.
2. Если наклонные равны, то равны и их проекции, и наоборот.
3. Большей наклонной соответствует большая проекция и наоборот.